
Point reflection
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a point reflection or inversion in a point (or inversion through a point, or central inversion) is a type of isometry
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. An object that is invariant under a point reflection is said to possess point symmetry; if it is invariant under point reflection through its center, it is said to possess central symmetry or to be centrally symmetric.
Terminology
The term "reflection" is loose, and considered by some an abuse of language, with "inversion" preferred; however, "point reflection" is widely used. Such maps are involutions, meaning that they have order 2 – they are their own inverse: doing them twice yields the identity mapIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
– which is also true of other maps called "reflections". More narrowly, a "reflection" refers to a reflection in a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
(
 dimensional affine subspace – a point on the line
dimensional affine subspace – a point on the lineLine
- Science and technology :* Line , a circuit or loop.** A power line for electric power transmission** line power or lines power, domestic mains electricity.** telephone line** RF transmission line...
, a line in the plane, a plane in 3-space), with the hyperplane being fixed, but more broadly "reflection" is applied to any involution of Euclidean space, and the fixed set (an affine space of dimension k, where
 ) is called the "mirror". In dimension 1 these coincide, as a point is a hyperplane in the line.
) is called the "mirror". In dimension 1 these coincide, as a point is a hyperplane in the line.In terms of linear algebra, assuming the origin is fixed, involutions are exactly the diagonalizable maps with all eigenvalues either 1 or −1. Reflection in a hyperplane has a single −1 eigenvalue (and multiplicity
 on the 1 eigenvalue), while point reflection has only the −1 eigenvalue (with multiplicity n).
on the 1 eigenvalue), while point reflection has only the −1 eigenvalue (with multiplicity n).The term "inversion" should not be confused with inversive geometry, where "inversion" is defined with respect to a circle
Examples
In two dimensions, a point reflection is the same as a rotationRotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
of 180 degrees. In three dimensions, a point reflection can be described as a 180-degree rotation composed with reflection across a plane perpendicular to the axis of rotation. In dimension n, point reflections are orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
-preserving if n is even, and orientation-reversing if n is odd.
Of the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, all but the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
are centrally symmetric.
Formula
Given a vector a in the Euclidean space Rn, the formula for the reflection of a across the point p is
In the case where p is the origin, point reflection is simply the negation of the vector a (see reflection through the origin).
In Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the inversion of a point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
X in respect to a point P is a point X* such that P is the midpoint of the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
with endpoints X and X*. In other words, the vector from X to P is the same as the vector from P to X*.
The formula for the inversion in P is
- x*=2a−x
where a, x and x* are the position vectors of P, X and X* respectively.
This mapping
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is an isometric
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
involutive affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
which has exactly one fixed point
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, which is P.
Point reflection group

Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
. Specifically, point reflection at p followed by point reflection at q is translation by the vector 2(q – p).
The set consisting of all point reflections and translations is Lie subgroup
Lie subgroup
In mathematics, a Lie subgroup H of a Lie group G is a Lie group that is a subset of G and such that the inclusion map from H to G is an injective immersion and group homomorphism. According to Cartan's theorem, a closed subgroup of G admits a unique smooth structure which makes it an embedded Lie...
of the Euclidean group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
. It is a semidirect product
Semidirect product
In mathematics, specifically in the area of abstract algebra known as group theory, a semidirect product is a particular way in which a group can be put together from two subgroups, one of which is a normal subgroup. A semidirect product is a generalization of a direct product...
of Rn with a cyclic group
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
of order 2, the latter acting on Rn by negation. It is precisely the subgroup of the Euclidean group that fixes the line at infinity
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
pointwise.
In the case n = 1, the point reflection group is the full isometry group
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
of the line.
Point reflections in mathematics
- Point reflection across the center of a sphere yields the antipodal map.
- A symmetric spaceRiemannian symmetric spaceIn differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
is a Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
with an isometric reflection across each point. Symmetric spaces play an important role in the study of Lie groupLie groupIn mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and Riemannian geometryRiemannian geometryRiemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
.
Properties
In even-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, say 2N-dimensional space, the inversion in a point P is equivalent to N rotations over angles π in each plane of an arbitrary set of N mutually orthogonal planes intersecting at P. These rotations are mutually commutative. Therefore inversion in a point in even-dimensional space is an orientation-preserving isometry or direct isometry
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
.
In odd-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, say (2N + 1)-dimensional space, it is equivalent to N rotations over π in each plane of an arbitrary set of N mutually orthogonal planes intersecting at P, combined with the reflection in the 2N-dimensional subspace spanned by these rotation planes.
Therefore it reverses rather than preserves orientation
Orientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
, it is an indirect isometry
Euclidean group
In mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
.
Geometrically in 3D it amounts to rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
about an axis through P by an angle of 180°, combined with reflection in the plane through P which is perpendicular to the axis; the result does not depend on the orientation
Orientation (rigid body)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
(in the other sense) of the axis. Notations for the type of operation, or the type of group it generates, are
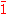 , Ci, S2, and 1×. The group type is one of the three symmetry group
, Ci, S2, and 1×. The group type is one of the three symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
types in 3D without any pure rotational symmetry
Rotational symmetry
Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...
, see cyclic symmetries
Cyclic symmetries
This article deals with the four infinite series of point groups in three dimensions with n-fold rotational symmetry about one axis , and no other rotational symmetry :Chiral:*Cn of order n - n-fold rotational symmetry...
with n=1.
The following point groups in three dimensions
Point groups in three dimensions
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
contain inversion:
- Cnh and Dnh for even n
- S2n and Dnd for odd n
- Th, Oh, and Ih
Closely related to inverse in a point is reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
in respect to a plane, which can be thought of as a "inversion in a plane".
Inversion with respect to the origin
Inversion with respect to the origin corresponds to additive inversionAdditive inverse
In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....
of the position vector, and also to scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by −1. The operation commutes with every other linear transformation
Linear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
, but not with translation
Translation (geometry)
In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...
: it is in the central
Center (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of the general linear group
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. "Inversion" without indicating "in a point", "in a line" or "in a plane", means this inversion; in physics 3-dimensional reflection through the origin is also called a parity transformation
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
.
In mathematics, reflection through the origin refers to the point reflection of Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn across the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
of the Cartesian coordinate system
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
. Reflection through the origin is an orthogonal transformation corresponding to scalar multiplication
Scalar multiplication
In mathematics, scalar multiplication is one of the basic operations defining a vector space in linear algebra . In an intuitive geometrical context, scalar multiplication of a real Euclidean vector by a positive real number multiplies the magnitude of the vector without changing its direction...
by
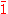 , and can also be written as
, and can also be written as  , where
, where 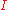 is the identity matrix
is the identity matrixIdentity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. In three dimensions, this sends
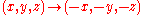 , and so forth.
, and so forth.Representations
As a scalar matrix, it is represented in every basis by a matrix with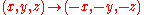 on the diagonal, and, together with the identity, is the center
on the diagonal, and, together with the identity, is the centerCenter (group theory)
In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
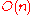 .
.It is a product of n orthogonal reflections (reflection through the axes of any orthogonal basis
Orthogonal basis
In mathematics, particularly linear algebra, an orthogonal basis for an inner product space is a basis for whose vectors are mutually orthogonal...
); note that orthogonal reflections commute.
In 2 dimensions, it is in fact rotation by 180 degrees, and in dimension
 , it is rotation by 180 degrees in n orthogonal planes;"Orthogonal planes" meaning all elements are orthogonal and the planes intersect at 0 only, not that they intersect in a line and have dihedral angle
, it is rotation by 180 degrees in n orthogonal planes;"Orthogonal planes" meaning all elements are orthogonal and the planes intersect at 0 only, not that they intersect in a line and have dihedral angleDihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
90°. note again that rotations in orthogonal planes commute.
Properties
It has determinant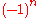 (from the representation by a matrix or as a product of reflections). Thus it is orientation-preserving in even dimension, thus an element of the special orthogonal group SO(2n), and it is orientation-reversing in odd dimension, thus not an element of SO(2n+1) and instead providing a splitting of the map
(from the representation by a matrix or as a product of reflections). Thus it is orientation-preserving in even dimension, thus an element of the special orthogonal group SO(2n), and it is orientation-reversing in odd dimension, thus not an element of SO(2n+1) and instead providing a splitting of the map  , showing that
, showing that 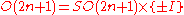 as an internal direct product.
as an internal direct product.- Together with the identity, it forms the centerCenter (group theory)In abstract algebra, the center of a group G, denoted Z,The notation Z is from German Zentrum, meaning "center". is the set of elements that commute with every element of G. In set-builder notation,...
of the orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. - It preserves every quadratic form, meaning
 , and thus is an element of every indefinite orthogonal group as well.
, and thus is an element of every indefinite orthogonal group as well. - It equals the identity if and only if the characteristic is 2.
- It is the longest elementLongest element of a Coxeter groupIn mathematics, the longest element of a Coxeter group is the unique element of maximal length in a finite Coxeter group with respect to the chosen generating set consisting of simple reflections. It is often denoted by w0...
of the Coxeter groupCoxeter groupIn mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
of signed permutations.
Analogously, it is a longest element of the orthogonal group, with respect to the generating set of reflections: elements of the orthogonal group all have length
Length function
In mathematical field of geometric group theory, a length function is a function that assigns a number to each element of a group.-Definition:...
at most n with respect to the generating set of reflections,This follows by classifying orthogonal transforms as direct sums of rotations and reflections, which follows from the spectral theorem
Spectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
, for instance. and reflection through the origin has length n, though it is not unique in this: other maximal combinations of rotations (and possibly reflections) also have maximal length.
Geometry
In SO(2r), reflection through the origin is the farthest point from the identity element with respect to the usual metric. In O(2r+1), reflection through the origin is not in SO(2r+1) (it is in the non-identity component), and there is no natural sense in which it is a "farther point" than any other point in the non-identity component, but it does provide a base point in the other component.Clifford algebras, Spin groups, and Pin groups
It should not be confused with the element in the Spin group. This is particularly confusing for even Spin groups, as
in the Spin group. This is particularly confusing for even Spin groups, as  , and thus in
, and thus in  there is both
there is both  and 2 lifts of
and 2 lifts of  .
.Reflection through the identity extends to an automorphism of a Clifford algebra
Clifford algebra
In mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
, called the main involution or grade involution.
Reflection through the identity lifts to a pseudoscalar.
See also
- Affine involutionAffine involutionIn Euclidean geometry, of special interest are involutions which are linear or affine transformations over the Euclidean space Rn. Such involutions are easy to characterize and they can be described geometrically.-Linear involutions:...
- Circle inversion
- Clifford algebraClifford algebraIn mathematics, Clifford algebras are a type of associative algebra. As K-algebras, they generalize the real numbers, complex numbers, quaternions and several other hypercomplex number systems. The theory of Clifford algebras is intimately connected with the theory of quadratic forms and orthogonal...
- Congruence (geometry)Congruence (geometry)In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
- Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
- Orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
- Parity (physics)Parity (physics)In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
- Reflection (mathematics)Reflection (mathematics)In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
- Riemannian symmetric spaceRiemannian symmetric spaceIn differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
- Spin group

