
Spontaneous symmetry breaking
Encyclopedia
Spontaneous symmetry breaking is the process by which a system described in a theoretically symmetrical way ends up in an apparently asymmetric state.
Though the process in itself is interesting from a mathematical point of view, it is fairly simple. Its notoriety outside the mathematical community stems from its established role in the standard model
of particle physics. In the context of its role within the standard model, it is more complicated (because it further involves the so-called
Higgs mechanism
—and the standard model itself is a complicated theory).
1, and the others with probability 0, they are no longer symmetric.
Hence, the symmetry is said to be spontaneously broken in that theory.
Nevertheless, the fact that each outcome is equally likely is a reflection of
the underlying symmetry, which is thus often dubbed "hidden symmetry", and has
crucial formal consequences, such as the presence of Nambu-Goldstone bosons.
, but requires that one element of the group is distinct, then spontaneous symmetry breaking has occurred. The theory must not dictate which member is distinct, only that one is. From this point on, the theory can be treated as if this element actually is distinct, with the proviso that any results found in this way must be resymmetrized, by taking the average of each of the elements of the group being the distinct one.
of elementary particle interactions predicts the existence of a number of particles. However, some particles (the W and Z bosons
) would then be predicted to be massless, when, in reality, they are observed to have mass. (This would appear to be a major failing of the theory.) To overcome this, the combination of spontaneous symmetry breaking in conjunction with the Higgs mechanism
gives these particles mass. It also suggests the presence of a new, as yet undetected particle, the Higgs boson
.
If the Higgs boson is not found, it will mean that the simplest implementation of the Higgs mechanism and spontaneous symmetry breaking as they are currently formulated are invalid, requiring an alternative model implementation of SSB and the Higgs mechanism operative in the accepted theory of electroweak interactions.
A detailed presentation of the Higgs mechanism is given in the article on the Yukawa interaction
, illustrating how it further gives mass to fermion
s.
in the absence of the Higgs mechanism, massless Goldstone boson
s arise.
The symmetry group can be discrete, such as the space group
of a crystal, or continuous (e.g., a Lie group
), such as the rotational symmetry of space. However, if the system contains only a single spatial dimension, then only discrete symmetries may be broken in a vacuum state
of the full quantum theory
, although a classical solution may break a continuous symmetry.
. In physics, one way of seeing spontaneous symmetry breaking is through the use of Lagrangian
s. Lagrangians, which essentially dictate how a system behaves, can be split up into kinetic and potential terms,
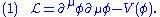
It is in this potential term (V(Φ)) that the symmetry breaking occurs. An example of a potential is illustrated in the graph at the right.
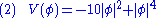
This potential has an infinite number of possible minima (vacuum states) given by
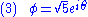
for any real θ between 0 and 2π. The system also has an unstable vacuum state corresponding to Φ = 0. This state has a U(1)
symmetry. However, once the system falls into a specific stable vacuum state (amounting to a choice of θ), this symmetry will appear to be lost, or "spontaneously broken".
In fact, any other choice of θ would have exactly the same energy, implying the existence of a massless Nambu-Goldstone boson
, the mode running around the circle at the minimum of this potential, and indicating there is some memory of the original symmetry in the Lagrangian.
awarded the 2008 Nobel Prize in Physics
to two Japanese citizens and a Japanese-born American for their work in subatomic physics symmetry breaking. American Yoichiro Nambu
, 87, of the University of Chicago
, won half of the prize for the discovery of the mechanism of spontaneous broken symmetry in the context of the strong interactions. (Japanese physicists Makoto Kobayashi
and Toshihide Maskawa
shared the other half of the prize for discovering the origin of the explicit breaking of CP symmetry in the weak interactions. This origin is ultimately reliant on the Higgs mechanism, but, so far understood as a "just so" feature of Higgs couplings, not a spontaneously broken symmetry phenomenon.)
Though the process in itself is interesting from a mathematical point of view, it is fairly simple. Its notoriety outside the mathematical community stems from its established role in the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics. In the context of its role within the standard model, it is more complicated (because it further involves the so-called
Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
—and the standard model itself is a complicated theory).
Illustration
For spontaneous symmetry breaking to occur, there must be a system in which there are several equally likely outcomes. The system as a whole is therefore symmetric with respect to these outcomes (if we consider any two outcomes, the probability is the same). However, if the system is sampled (i.e. if the system is actually used or interacted with in any way), a specific outcome must occur. Though we know the system as a whole is symmetric, we also see that it is never encountered with this symmetry, only in one specific state. Because one of the outcomes is always found with probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
1, and the others with probability 0, they are no longer symmetric.
Hence, the symmetry is said to be spontaneously broken in that theory.
Nevertheless, the fact that each outcome is equally likely is a reflection of
the underlying symmetry, which is thus often dubbed "hidden symmetry", and has
crucial formal consequences, such as the presence of Nambu-Goldstone bosons.
Formal point of view
When a theory is symmetric with respect to a symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
, but requires that one element of the group is distinct, then spontaneous symmetry breaking has occurred. The theory must not dictate which member is distinct, only that one is. From this point on, the theory can be treated as if this element actually is distinct, with the proviso that any results found in this way must be resymmetrized, by taking the average of each of the elements of the group being the distinct one.
Everyday example
A common example to help explain this phenomenon is a ball sitting on top of a hill. This ball is in a completely symmetric state. It could move in various directions or it could sit and mark time. However, its state is unstable because it might move in some direction: the slightest perturbing force will cause the ball to roll down the hill. When the ball comes out of its unstable, symmetric state by moving symmetry has been broken, because the direction in which the ball rolled has a visible feature that distinguishes it from all other directions. The "choice" of direction is immaterial, however, as any other direction would do, i.e. the system is still bearing traces of the symmetry of the hill, albeit now somewhat less apparent.Importance in the standard model
Without spontaneous symmetry breaking, the Standard ModelStandard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of elementary particle interactions predicts the existence of a number of particles. However, some particles (the W and Z bosons
W and Z bosons
The W and Z bosons are the elementary particles that mediate the weak interaction; their symbols are , and . The W bosons have a positive and negative electric charge of 1 elementary charge respectively and are each other's antiparticle. The Z boson is electrically neutral and its own...
) would then be predicted to be massless, when, in reality, they are observed to have mass. (This would appear to be a major failing of the theory.) To overcome this, the combination of spontaneous symmetry breaking in conjunction with the Higgs mechanism
Higgs mechanism
In particle physics, the Higgs mechanism is the process in which gauge bosons in a gauge theory can acquire non-vanishing masses through absorption of Nambu-Goldstone bosons arising in spontaneous symmetry breaking....
gives these particles mass. It also suggests the presence of a new, as yet undetected particle, the Higgs boson
Higgs boson
The Higgs boson is a hypothetical massive elementary particle that is predicted to exist by the Standard Model of particle physics. Its existence is postulated as a means of resolving inconsistencies in the Standard Model...
.
If the Higgs boson is not found, it will mean that the simplest implementation of the Higgs mechanism and spontaneous symmetry breaking as they are currently formulated are invalid, requiring an alternative model implementation of SSB and the Higgs mechanism operative in the accepted theory of electroweak interactions.
A detailed presentation of the Higgs mechanism is given in the article on the Yukawa interaction
Yukawa interaction
In particle physics, Yukawa's interaction, named after Hideki Yukawa, is an interaction between a scalar field \phi and a Dirac field \Psi of the typeV \approx g\bar\Psi \phi \Psi or g \bar \Psi \gamma^5 \phi \Psi ....
, illustrating how it further gives mass to fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
s.
Technical usage within physics
The crucial concept here is the order parameter. If there is a field (often a background field) which acquires an expectation value (not necessarily a vacuum expectation value) which is not invariant under the symmetry in question, we say that the system is in the ordered phase, and the symmetry is spontaneously broken. This is because other subsystems interact with the order parameter which forms a "frame of reference" to be measured against, so to speak. In that case, the vacuum state does not obey the initial symmetry (which would put it in the Wigner mode), and, instead has the (hidden) symmetry implemented in the Nambu-Goldstone mode. Normally,in the absence of the Higgs mechanism, massless Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
s arise.
The symmetry group can be discrete, such as the space group
Space group
In mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
of a crystal, or continuous (e.g., a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
), such as the rotational symmetry of space. However, if the system contains only a single spatial dimension, then only discrete symmetries may be broken in a vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
of the full quantum theory
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, although a classical solution may break a continuous symmetry.
Mathematical example: the Mexican hat potential
In the simplest idealized relativistic model, the spontaneously broken field is described through a scalar field theoryScalar field theory
In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields. A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field...
. In physics, one way of seeing spontaneous symmetry breaking is through the use of Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
s. Lagrangians, which essentially dictate how a system behaves, can be split up into kinetic and potential terms,
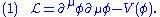
It is in this potential term (V(Φ)) that the symmetry breaking occurs. An example of a potential is illustrated in the graph at the right.
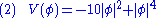
This potential has an infinite number of possible minima (vacuum states) given by
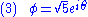
for any real θ between 0 and 2π. The system also has an unstable vacuum state corresponding to Φ = 0. This state has a U(1)
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
symmetry. However, once the system falls into a specific stable vacuum state (amounting to a choice of θ), this symmetry will appear to be lost, or "spontaneously broken".
In fact, any other choice of θ would have exactly the same energy, implying the existence of a massless Nambu-Goldstone boson
Goldstone boson
In particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
, the mode running around the circle at the minimum of this potential, and indicating there is some memory of the original symmetry in the Lagrangian.
Other examples
- For ferromagnetic materials, the underlying laws are invariant under spatial rotations. Here, the order parameter is the magnetizationMagnetizationIn classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
, which measures the magnetic dipole density. Above the Curie temperature, the order parameter is zero, which is spatially invariant, and there is no symmetry breaking. Below the Curie temperature, however, the magnetization acquires a constant nonvanishing value, which points in a certain direction (in the idealized situation where we have full equilibrium; otherwise, translational symmetry gets broken as well). The residual rotational symmetries which leave the orientation of this vector invariant remain unbroken, unlike the other rotations which do not and are thus spontaneously broken. - The laws describing a solid are invariant under the full Euclidean groupEuclidean groupIn mathematics, the Euclidean group E, sometimes called ISO or similar, is the symmetry group of n-dimensional Euclidean space...
, but the solid itself spontaneously breaks this group down to a space groupSpace groupIn mathematics and geometry, a space group is a symmetry group, usually for three dimensions, that divides space into discrete repeatable domains.In three dimensions, there are 219 unique types, or counted as 230 if chiral copies are considered distinct...
. The displacement and the orientation are the order parameters. - General relativity has a Lorenz symmetry, but in FRW cosmological models, the mean 4-velocity field defined by averaging over the velocities of the galaxies (the galaxies act like gas particles at cosmological scales) acts as an order parameter breaking this symmetry. Similar comments can be made about the cosmic microwave background.
- For the electroweak model, as explained earlier, a component of the Higgs field provides the order parameter breaking the electroweak gauge symmetry to the electromagnetic gauge symmetry. Like the ferromagnetic example, there is a phase transition at the electroweak temperature. The same comment about us not tending to notice broken symmetries suggests why it took so long for us to discover electroweak unification.
- In superconductors, there is a condensed-matter collective field ψ, which acts as the order parameter breaking the electromagnetic gauge symmetry.
- Take a thin cylindrical plastic rod and push both ends together. Before buckling, the system is symmetric under rotation, and so visibly cylindrically symmetric. But after buckling, it looks different, and asymmetric. Nevertheless, features of the cylindrical symmetry are still there: ignoring friction, it would take no force to freely spin the rod around, displacing the ground state in time, and amounting to an oscillation of vanishing frequency, unlike the radial oscillations in the direction of the buckle. This spinning mode is effectively the requisite Nambu-Goldstone bosonGoldstone bosonIn particle and condensed matter physics, Goldstone bosons or Nambu–Goldstone bosons are bosons that appear necessarily in models exhibiting spontaneous breakdown of continuous symmetries...
. - Consider a uniform layer of fluidFluidIn physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
over an infinite horizontal plane. This system has all the symmetries of the Euclidean plane. But now heat the bottom surface uniformly so that it becomes much hotter than the upper surface. When the temperature gradient becomes large enough, convection cellConvection cellA convection cell is a phenomenon of fluid dynamics that occurs in situations where there are density differences within a body of liquid or gas. The convection usually requires a gravitational field but in microgravity experiments, thermal convection has been observed without gravitational effects...
s will form, breaking the Euclidean symmetry. - Consider a bead on a circular hoop that is rotated about a vertical diameterDiameterIn geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
. As the rotational velocity is increased gradually from rest, the bead will initially stay at its initial equilibrium point at the bottom of the hoop (intuitively stable, lowest gravitational potential). At a certain critical rotational velocity, this point will become unstable and the bead will jump to one of two other newly created equilibria, equidistantEquidistantA point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.In two-dimensional Euclidian geometry the locus of points equidistant from two given points is their perpendicular bisector...
from the center. Initially, the system is symmetric with respect to the diameter, yet after passing the critical velocity, the bead ends up in one of the two new equilibrium points, thus breaking the symmetry. Note: This can easily be tried at home with an electric drill, a marble, and a pot cover, (or any other combination you can think of).
Nobel Prize
On October 7, 2008, the Royal Swedish Academy of SciencesRoyal Swedish Academy of Sciences
The Royal Swedish Academy of Sciences or Kungliga Vetenskapsakademien is one of the Royal Academies of Sweden. The Academy is an independent, non-governmental scientific organization which acts to promote the sciences, primarily the natural sciences and mathematics.The Academy was founded on 2...
awarded the 2008 Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
to two Japanese citizens and a Japanese-born American for their work in subatomic physics symmetry breaking. American Yoichiro Nambu
Yoichiro Nambu
is a Japanese-born American physicist, currently a professor at the University of Chicago. Known for his contributions to the field of theoretical physics, he was awarded a one-half share of the Nobel Prize in Physics in 2008 for the discovery of the mechanism of spontaneous broken symmetry in...
, 87, of the University of Chicago
University of Chicago
The University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
, won half of the prize for the discovery of the mechanism of spontaneous broken symmetry in the context of the strong interactions. (Japanese physicists Makoto Kobayashi
Makoto Kobayashi (physicist)
is a Japanese physicist known for his work on CP-violation who was awarded one quarter of the 2008 Nobel Prize in Physics "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature."- Biography :After completing his PhD at...
and Toshihide Maskawa
Toshihide Maskawa
is a Japanese theoretical physicist known for his work on CP-violation who was awarded one quarter of the 2008 Nobel Prize in Physics "for the discovery of the origin of the broken symmetry which predicts the existence of at least three families of quarks in nature."-Biography:A native of Aichi...
shared the other half of the prize for discovering the origin of the explicit breaking of CP symmetry in the weak interactions. This origin is ultimately reliant on the Higgs mechanism, but, so far understood as a "just so" feature of Higgs couplings, not a spontaneously broken symmetry phenomenon.)
See also
External links
- Spontaneous symmetry breaking
- Physical Review Letters - 50th Anniversary Milestone Papers
- In CERN Courier, Steven Weinberg reflects on spontaneous symmetry breaking
- Englert-Brout-Higgs-Guralnik-Hagen-Kibble Mechanism on Scholarpedia
- History of Englert-Brout-Higgs-Guralnik-Hagen-Kibble Mechanism on Scholarpedia
- The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- International Journal of Modern Physics A: The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles
- Guralnik, G S; Hagen, C R and Kibble, T W B (1967). Broken Symmetries and the Goldstone Theorem. Advances in Physics, vol. 2 Interscience Publishers, New York. pp. 567-708 ISBN 0470170573
- Spontaneous Symmetry Breaking in Gauge Theories: a Historical Survey

