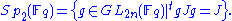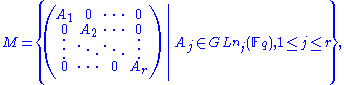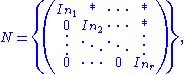Representation of a Lie group
Encyclopedia
In mathematics
and theoretical physics
, the idea of a representation of a Lie group
plays an important role in the study of continuous symmetry
. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie algebras. The physics literature sometimes passes over the distinction between Lie group representations and Lie algebra representations.
of a Lie group
G on a finite-dimensional complex vector space
V is a smooth group homomorphism
Ψ:G→Aut(V) from G to the automorphism group of V.
For n-dimensional V, the automorphism group of V is identified with a subset of complex square-matrices of order n. The automorphism group of V is given the structure of a smooth manifold using this identification. The condition that Ψ is smooth, in the definition above, means that Ψ is a smooth map from the smooth manifold G to the smooth manifold Aut(V).
If a basis for the complex vector space V is chosen, the representation can be expressed as a homomorphism into GL(n,C)
. This is known as a matrix representation.
of a Lie group
G on a vector space
V (over a field
K) is a smooth
(i.e. respecting the differential structure) group homomorphism
G→Aut(V) from G to the automorphism group of V. If a basis for the vector space V is chosen, the representation can be expressed as a homomorphism into GL(n,K)
. This is known as a matrix representation.
Two representations of G on vector spaces V, W are equivalent if they have the
same matrix representations with respect to some choices of bases
for V and W.
On the Lie algebra level, there is a corresponding linear mapping from the Lie algebra of G to End(V)
preserving the Lie bracket
[ , ]. See representation of Lie algebras for the Lie algebra theory.
If the homomorphism is in fact a monomorphism
, the representation is said to be faithful.
A unitary representation
is defined in the same way, except that G maps to unitary matrices; the Lie algebra will then map to skew-hermitian
matrices.
If G is a compact Lie group, every finite-dimensional representation is equivalent to
a unitary one.
of a Lie group
G on a complex Hilbert space
V is a group homomorphism
Ψ:G → B(V) from G to B(V), the group of bounded linear operators of V which have a bounded inverse, such that the map G×V → V given by (g,v) → Ψ(g)v is continuous.
This definition can handle representations on infinite-dimensional Hilbert spaces. Such representations can be found in e.g. quantum mechanics, but also in Fourier analysis as shown in the following example.
Let G=R, and let the complex Hilbert space V be L2(R). We define the representation Ψ:R → B(L2(R)) by Ψ(r){f(x)} → f(r-1x).
See also Wigner's classification
for representations of the Poincaré group
.
; the allowable (dominant) highest weights satisfy a suitable positivity condition. In particular, there exists a set of fundamental weights, indexed by the vertices of the Dynkin diagram of G, such that dominant weights are simply non-negative integer linear combinations of the fundamental weights. The characters of the irreducible representations are given by the Weyl character formula
.
If G is a commutative Lie group
, then its irreducible representations are simply the continuous character
s of G: see Pontryagin duality
for this case.
A quotient representation is a quotient module
of the group ring
.
, where In is the n×n identity matrix. Let
Then Sp(2,Fq) is a symplectic group of rank n and is a finite group of Lie type. For G = GL(n, Fq) or SL(n, Fq) (and some other examples), the standard Borel subgroup B of G is the subgroup of G consisting of the upper triangular elements in G. A standard parabolic subgroup of G is a subgroup of G which contains the standard Borel subgroup B. If P is a standard parabolic subgroup of GL(n, Fq), then there exists a partition (n1, …, nr) of n (a set of positive integers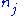
such that 
) such that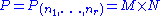 
, where 
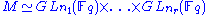has the form
and
where
denotes arbitrary entries in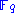 
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, the idea of a representation of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
plays an important role in the study of continuous symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. A great deal is known about such representations, a basic tool in their study being the use of the corresponding 'infinitesimal' representations of Lie algebras. The physics literature sometimes passes over the distinction between Lie group representations and Lie algebra representations.
Representations on a complex finite-dimensional vector space
Let us first discuss representations acting on finite-dimensional complex vector spaces. A representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G on a finite-dimensional complex vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V is a smooth group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
Ψ:G→Aut(V) from G to the automorphism group of V.
For n-dimensional V, the automorphism group of V is identified with a subset of complex square-matrices of order n. The automorphism group of V is given the structure of a smooth manifold using this identification. The condition that Ψ is smooth, in the definition above, means that Ψ is a smooth map from the smooth manifold G to the smooth manifold Aut(V).
If a basis for the complex vector space V is chosen, the representation can be expressed as a homomorphism into GL(n,C)
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. This is known as a matrix representation.
Representations on a finite-dimensional vector space over an arbitrary field
A representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G on a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
V (over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K) is a smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
(i.e. respecting the differential structure) group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
G→Aut(V) from G to the automorphism group of V. If a basis for the vector space V is chosen, the representation can be expressed as a homomorphism into GL(n,K)
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
. This is known as a matrix representation.
Two representations of G on vector spaces V, W are equivalent if they have the
same matrix representations with respect to some choices of bases
for V and W.
On the Lie algebra level, there is a corresponding linear mapping from the Lie algebra of G to End(V)
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
preserving the Lie bracket
Lie bracket
Lie bracket can refer to:*A bilinear binary operation defined on elements of a Lie algebra*Lie bracket of vector fields...
[ , ]. See representation of Lie algebras for the Lie algebra theory.
If the homomorphism is in fact a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, the representation is said to be faithful.
A unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
is defined in the same way, except that G maps to unitary matrices; the Lie algebra will then map to skew-hermitian
Skew-Hermitian
An anti-Hermitian, skew-Hermitian, or skew-adjoint operator or matrix is one whose adjoint is the negative of itself:A^*=-A \, Imaginary numbers can be thought of as skew-adjoint , whereas real numbers correspond to self-adjoint operators....
matrices.
If G is a compact Lie group, every finite-dimensional representation is equivalent to
a unitary one.
Representations on Hilbert spaces
A representationGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
G on a complex Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
V is a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
Ψ:G → B(V) from G to B(V), the group of bounded linear operators of V which have a bounded inverse, such that the map G×V → V given by (g,v) → Ψ(g)v is continuous.
This definition can handle representations on infinite-dimensional Hilbert spaces. Such representations can be found in e.g. quantum mechanics, but also in Fourier analysis as shown in the following example.
Let G=R, and let the complex Hilbert space V be L2(R). We define the representation Ψ:R → B(L2(R)) by Ψ(r){f(x)} → f(r-1x).
See also Wigner's classification
Wigner's classification
In mathematics and theoretical physics, Wigner's classificationis a classification of the nonnegative energy irreducible unitary representations of the Poincaré group, which have sharp mass eigenvalues...
for representations of the Poincaré group
Poincaré group
In physics and mathematics, the Poincaré group, named after Henri Poincaré, is the group of isometries of Minkowski spacetime.-Simple explanation:...
.
Classification
If G is a semisimple group, its finite-dimensional representations can be decomposed as direct sums of irreducible representations. The irreducibles are indexed by highest weightWeight (representation theory)
In the mathematical field of representation theory, a weight of an algebra A over a field F is an algebra homomorphism from A to F – a linear functional – or equivalently, a one dimensional representation of A over F. It is the algebra analogue of a multiplicative character of a group...
; the allowable (dominant) highest weights satisfy a suitable positivity condition. In particular, there exists a set of fundamental weights, indexed by the vertices of the Dynkin diagram of G, such that dominant weights are simply non-negative integer linear combinations of the fundamental weights. The characters of the irreducible representations are given by the Weyl character formula
Weyl character formula
In mathematics, the Weyl character formula in representation theory describes the characters of irreducible representations of compact Lie groups in terms of their highest weights. It was proved by ....
.
If G is a commutative Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
, then its irreducible representations are simply the continuous character
Character (mathematics)
In mathematics, a character is a special kind of function from a group to a field . There are at least two distinct, but overlapping meanings...
s of G: see Pontryagin duality
Pontryagin duality
In mathematics, specifically in harmonic analysis and the theory of topological groups, Pontryagin duality explains the general properties of the Fourier transform on locally compact groups, such as R, the circle or finite cyclic groups.-Introduction:...
for this case.
A quotient representation is a quotient module
Quotient module
In abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
of the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
.
Formulaic examples
Let Fq be a finite field of order q and characteristic p. Let G be a finite group of Lie type, that is, G is the Fq-rational points of a connected reductive group G defined over Fq. For example, if n is a positive integer GL(n, Fq) and SL(n, Fq) are finite groups of Lie type. Let, where In is the n×n identity matrix. Let
Then Sp(2,Fq) is a symplectic group of rank n and is a finite group of Lie type. For G = GL(n, Fq) or SL(n, Fq) (and some other examples), the standard Borel subgroup B of G is the subgroup of G consisting of the upper triangular elements in G. A standard parabolic subgroup of G is a subgroup of G which contains the standard Borel subgroup B. If P is a standard parabolic subgroup of GL(n, Fq), then there exists a partition (n1, …, nr) of n (a set of positive integers
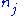such that ) such that 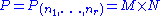, where 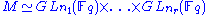has the form
and
where
denotes arbitrary entries in 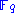.See also
- Representation theory of Hopf algebras
- Adjoint representation of a Lie group
- List of Lie group topics