
Conserved current
Encyclopedia
In physics
a conserved current is a current,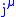 , that satisfies the continuity equation
, that satisfies the continuity equation
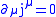 . The continuity equation represents a conservation law, hence the name.
. The continuity equation represents a conservation law, hence the name.
Indeed, integrating the continuity equation over a volume , large enough to have no currents through its surface, leads to the conservation law
, large enough to have no currents through its surface, leads to the conservation law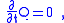
where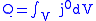 is the conserved quantity.
is the conserved quantity.
In gauge theories
the gauge fields couple to conserved currents. For example, the electromagnetic field
couples to the conserved electric current
.
translational symmetry
. The continuity equation
for the conserved current is a statement of a conservation law
.
Examples of canonical conjugate quantities are:
Conserved currents play an extremely important role in theoretical physics
, because Noether's theorem
connects the existence of a conserved current to the existence of a symmetry
of some quantity in the system under study. In practical terms, all conserved currents are Noether currents, as the existence of a conserved current implies the existence of a symmetry. Conserved currents play an important role in the theory of partial differential equation
s, as the existence of a conserved current points to the existence of constants of motion, which are required to define a foliation
and thus an integrable system
. The conservation law is expressed as the vanishing of a 4-divergence
, where the Noether charge forms the zeroth component of the 4-current
.
,

where:
ρ is the free electric charge density (in units of C/m³)
J is the current density:
v is the velocity of the charges.
The equation would apply equally to masses (or other conserved quantities), where the word mass is substituted for the words electric charge above.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
a conserved current is a current,
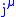 , that satisfies the continuity equation
, that satisfies the continuity equationContinuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
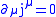 . The continuity equation represents a conservation law, hence the name.
. The continuity equation represents a conservation law, hence the name.Indeed, integrating the continuity equation over a volume
 , large enough to have no currents through its surface, leads to the conservation law
, large enough to have no currents through its surface, leads to the conservation law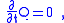
where
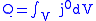 is the conserved quantity.
is the conserved quantity.In gauge theories
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
the gauge fields couple to conserved currents. For example, the electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
couples to the conserved electric current
Charge conservation
In physics, charge conservation is the principle that electric charge can neither be created nor destroyed. The net quantity of electric charge, the amount of positive charge minus the amount of negative charge in the universe, is always conserved...
.
Conserved quantities and symmetries
Conserved current is the flow of the canonical conjugate of a quantity possessing a continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
translational symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
. The continuity equation
Continuity equation
A continuity equation in physics is a differential equation that describes the transport of a conserved quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described...
for the conserved current is a statement of a conservation law
Conservation law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves....
.
Examples of canonical conjugate quantities are:
- TimeTimeTime is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
and energyEnergyIn physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
- the continuous translational symmetry of time implies the conservation of energyConservation of energyThe nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
. - SpaceSpaceSpace is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
and momentumMomentumIn classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
- the continuous translational symmetry of space implies the conservation of momentum - Space and angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
- the continuous rotational symmetry of space implies the conservation of angular momentum - Wave function phasePhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
and electric chargeElectric chargeElectric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
- the continuous phase angle symmetry of the wave function implies the conservation of electric charge
Conserved currents play an extremely important role in theoretical physics
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, because Noether's theorem
Noether's theorem
Noether's theorem states that any differentiable symmetry of the action of a physical system has a corresponding conservation law. The theorem was proved by German mathematician Emmy Noether in 1915 and published in 1918...
connects the existence of a conserved current to the existence of a symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of some quantity in the system under study. In practical terms, all conserved currents are Noether currents, as the existence of a conserved current implies the existence of a symmetry. Conserved currents play an important role in the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, as the existence of a conserved current points to the existence of constants of motion, which are required to define a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
and thus an integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
. The conservation law is expressed as the vanishing of a 4-divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
, where the Noether charge forms the zeroth component of the 4-current
Four-current
In special and general relativity, the four-current is the Lorentz covariant four-vector that replaces the electromagnetic current density, or indeed any conventional charge current density...
.
Conserved currents in electromagnetism
The conservation of charge, for example, in the notation of Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
,

where:
ρ is the free electric charge density (in units of C/m³)
J is the current density:
- J =
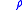 v
v
v is the velocity of the charges.
The equation would apply equally to masses (or other conserved quantities), where the word mass is substituted for the words electric charge above.

