T-symmetry
Encyclopedia
T Symmetry is the symmetry of physical laws
under a time
reversal transformation
:
Although in restricted contexts one may find this symmetry, the observable universe
itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics
.
Time asymmetries are generally distinguished as between those intrinsic to the dynamic laws of nature, and those due to the initial conditions of our universe
.
The T-asymmetry of the weak force is of the first kind, while the T-asymmetry of the second law of thermodynamics
is of the second kind.
For example, Maxwell's equations
with material absorption
or Newtonian mechanics with friction
are not time-reversal invariant at the macroscopic level where they are normally applied, even if they are invariant at the microscopic level when one includes the atomic motions the "lost" energy is translated into.
. Many other phenomena, such as the relative motion of bodies with friction, or viscous motion of fluids, reduce to this, because the underlying mechanism is the dissipation of usable energy (for example, kinetic energy) into heat.
Is this time-asymmetric dissipation really inevitable? This question has been considered by many physicists, often in the context of Maxwell's demon
. The name comes from a thought experiment
described by James Clerk Maxwell
in which a microscopic demon guards a gate between two halves of a room. It only lets slow molecules into one half, only fast ones into the other. By eventually making one side of the room cooler than before and the other hotter, it seems to reduce the entropy
of the room, and reverse the arrow of time. Many analyses have been made of this; all show that when the entropy of room and demon are taken together, this total entropy does increase. Modern analyses of this problem have taken into account Claude E. Shannon's relation between entropy and information
. Many interesting results in modern computing are closely related to this problem — reversible computing
, quantum computing and physical limits to computing, are examples. These seemingly metaphysical questions are today, in these ways, slowly being converted to the stuff of the physical sciences.
The current consensus hinges upon the Boltzmann-Shannon identification of the logarithm of phase space
volume with the negative of Shannon information
, and hence to entropy
. In this notion, a fixed initial state of a macroscopic system corresponds to relatively low entropy because the coordinates of the molecules of the body are constrained. As the system evolves in the presence of dissipation, the molecular coordinates can move into larger volumes of phase space, becoming more uncertain, and thus leading to increase in entropy.
One can, however equally well imagine a state of the universe in which the motions of all of the particles at one instant were the reverse (strictly, the CPT reverse). Such a state would then evolve in reverse, so presumably entropy would decrease (Loschmidt's paradox
). Why is 'our' state preferred over the other?
One position is to say that the constant increase of entropy we observe happens only because of the initial state of our universe. Other possible states of the universe (for example, a universe at heat death equilibrium) would actually result in no increase of entropy. In this view, the apparent T-asymmetry of our universe is a problem in cosmology
: why did the universe start with a low entropy? This view, if it remains viable in the light of future cosmological observation, would connect this problem to one of the big open questions beyond the reach of today's physics — the question of initial conditions of the universe.
of a black hole
from the outside, and then fall rapidly to the central region where our understanding of physics breaks down. Since within a black hole the forward light-cone is directed towards the center and the backward light-cone is directed outward, it is not even possible to define time-reversal in the usual manner. The only way anything can escape from a black hole is as Hawking radiation
.
The time reversal of a black hole would be a hypothetical object known as a white hole
. From the outside they appear similar. While a black hole has a beginning and is inescapable, a white hole has an ending and cannot be entered. The forward light-cones of a white hole are directed outward; and its backward light-cones are directed towards the center.
The event horizon of a black hole may be thought of as a surface moving outward at the local speed of light and is just on the edge between escaping and falling back. The event horizon of a white hole is a surface moving inward at the local speed of light and is just on the edge between being swept outward and succeeding in reaching the center. They are two different kinds of horizons—the horizon of a white hole is like the horizon of a black hole turned inside-out.
The modern view of black hole irreveresibility is to relate it to the second law of thermodynamics
, since black holes are viewed as thermodynamic objects
. Indeed, according to the Gauge-gravity duality conjecture, all microscopic processes in a black hole are reversible, and only the collective behavior is irreversible, as in any other macroscopic, thermal system.
Kinetic consequences: detailed balance
In physical and chemical kinetics
, T-symmetry of the mechanical microscopic equations implies two important laws: the principle of detailed balance
and the Onsager reciprocal relations
. T-symmetry of the microscopic description together with its kinetic consequences are called microscopic reversibility
.
, Position of a particle in three-space
, Acceleration of the particle
, Force on the particle
, Energy of the particle
, Electric potential (voltage)
, Electric field
, Electric displacement
, Density of electric charge
, Electric polarization
, The time when an event occurs
, Velocity of a particle
, Linear momentum of a particle
, Angular momentum of a particle (both orbital and spin)
, Electromagnetic vector potential
, Magnetic induction
, Magnetic field
, Density of electric current
, Magnetization
, Poynting vector
v. However, delicate experiments in which known sources of dissipation are removed reveal that the laws of mechanics are time reversal invariant. Dissipation itself is originated in the second law of thermodynamics
.
The motion of a charged body in a magnetic field, B involves the velocity through the Lorentz force
term v×B, and might seem at first to be asymmetric under T. A closer look assures us that B also changes sign under time reversal. This happens because a magnetic field is produced by an electric current, J, which reverses sign under T. Thus, the motion of classical charged particles in electromagnetic field
s is also time reversal invariant. (Despite this, it is still useful to consider the time-reversal non-invariance in a local sense when the external field is held fixed, as when the magneto-optic effect
is analyzed. This allows one to analyze the conditions under which optical phenomena that locally break time-reversal, such as Faraday isolators, can occur.) The laws of gravity also seem to be time reversal invariant in classical mechanics.
In physics
one separates the laws of motion, called kinematics
, from the laws of force, called dynamics
. Following the classical kinematics of Newton's laws of motion
, the kinematics of quantum mechanics
is built in such a way that it presupposes nothing about the time reversal symmetry of the dynamics. In other words, if the dynamics are invariant, then the kinematics will allow it to remain invariant; if the dynamics is not, then the kinematics will also show this. The structure of the quantum laws of motion are richer, and we examine these next.
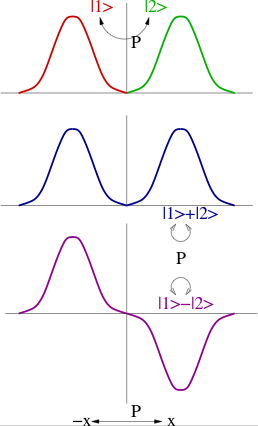This section contains a discussion of the three most important properties of time reversal in quantum mechanics; chiefly,
The strangeness of this result is clear if one compares it with parity. If parity transforms a pair of quantum states into each other, then the sum and difference of these two basis states are states of good parity. Time reversal does not behave like this. It seems to violate the theorem that all abelian group
s be represented by one dimensional irreducible representations. The reason it does this is that it is represented by an anti-unitary operator. It thus opens the way to spinor
s in quantum mechanics.
either by a unitary operator, S = U, or an antiunitary one, S = UK where U is unitary
, and K denotes complex conjugation. These are the only operations that acts on Hilbert space so as to preserve the length of the projection of any one state-vector onto another state-vector.
Consider the parity
operator. Acting on the position, it reverses the directions of space, so that P−1xP = −x. Similarly, it reverses the direction of momentum, so that PpP−1 = −p, where x and p are the position and momentum operators. This preserves the canonical commutator
[x, p] = iħ, where ħ is the reduced Planck constant, only if P is chosen to be unitary, PiP−1 = i.
On the other hand, for time reversal, the time-component of the momentum is the energy. If time reversal were implemented as a unitary operator, it would reverse the sign of the energy just as space-reversal reverses the sign of the momentum. This is not possible, because, unlike momentum, energy is always positive. Since energy in quantum mechanics is defined as the phase factor exp(-iEt) that one gets when one moves forward in time, the way to reverse time while preserving the sign of the energy is to reverse the sense of "i", so that the sense of phases is reversed.
Similarly, any operation that reverses the sense of phase, which changes the sign of i, will turn positive energies into negative energies unless it also changes the direction of time. So every antiunitary symmetry in a theory with positive energy must reverse the direction of time. The only antiunitary symmetry is time reversal, together with a unitary symmetry that does not reverse time.
Given the time reversal operator T, it does nothing to the x-operator, TxT−1 = x, but it reverses the direction of p, so that TpT−1 = −p. The canonical commutator is invariant only if T is chosen to be anti-unitary, i.e., TiT−1 = −i. For a particle
with spin, one can use the representation
where Sy is the y-component of the spin, to find that TJT−1 = −J.
(EDM) of any particle. The EDM is defined through the shift in the energy of a state when it is put in an external electric field: Δe = d·E + E·δ·E, where d is called the EDM and δ, the induced dipole moment. One important property of an EDM is that the energy shift due to it changes sign under a parity transformation. However, since d is a vector, its expectation value in a state |ψ> must be proportional to <ψ| J |ψ>. Thus, under time reversal, an invariant state must have vanishing EDM. In other words, a non-vanishing EDM signals both P and T symmetry-breaking.
It is interesting to examine this argument further, since one feels that some molecules, such as water, must have EDM irrespective of whether T is a symmetry. This is correct: if a quantum system has degenerate ground states that transform into each other under parity, then time reversal need not be broken to give EDM.
Experimentally observed bounds on the electric dipole moment of the nucleon
currently set stringent limits on the violation of time reversal symmetry in the strong interactions, and their modern theory: quantum chromodynamics
. Then, using the CPT invariance of a relativistic quantum field theory
, this puts strong bounds
on strong CP violation.
Experimental bounds on the electron electric dipole moment
also place limits on theories of particle physics and their parameters.
where Φ is a diagonal matrix of phases. As a result, U = ΦUT and UT = UΦ, showing that
This means that the entries in Φ are ±1, as a result of which one may have either T2 = ±1. This is specific to the anti-unitarity of T. For a unitary operator, such as the parity
, any phase is allowed.
Next, take a Hamiltonian invariant under T. Let |a> and T|a> be two quantum states of the same energy. Now, if T2 = −1, then one finds that the states are orthogonal: a result called Kramers' theorem. This implies that if T2 = −1, then there is a twofold degeneracy in the state. This result in non-relativistic quantum mechanics
presages the spin statistics theorem of quantum field theory
.
Quantum states that give unitary representations of time reversal, i.e., have T2=1, are characterized by a multiplicative quantum number
, sometimes called the T-parity.
Time reversal transformation for fermions in quantum field theories can be represented by an 8-component spinor in which the above mentioned T-parity can be a complex number with unit radius. The CPT invariance is not a theorem but a better to have property in these class of theories.
codified the basic laws of dynamics into the standard model
. This is formulated as a quantum field theory
that has CPT symmetry
, i.e., the laws are invariant under simultaneous operation of time reversal, parity
and charge conjugation. However, time reversal itself is seen not to be a symmetry (this is usually called CP violation
). There are two possible origins of this asymmetry, one through the mixing of different flavour
s of quarks in their weak decay
s, the second through a direct CP violation in strong interactions. The first is seen in experiments, the second is strongly constrained by the non-observation of the EDM of a neutron
.
It is important to stress that this time reversal violation is unrelated to the second law of thermodynamics
, because due to the conservation of the CPT symmetry
, the effect of time reversal is to rename particle
s as antiparticle
s and vice versa. Thus the second law of thermodynamics
is thought to originate in the initial conditions in the universe.
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
under a time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
reversal transformation
Transformation (mathematics)
In mathematics, a transformation could be any function mapping a set X on to another set or on to itself. However, often the set X has some additional algebraic or geometric structure and the term "transformation" refers to a function from X to itself that preserves this structure.Examples include...
:
Although in restricted contexts one may find this symmetry, the observable universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
.
Time asymmetries are generally distinguished as between those intrinsic to the dynamic laws of nature, and those due to the initial conditions of our universe
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
.
The T-asymmetry of the weak force is of the first kind, while the T-asymmetry of the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
is of the second kind.
Invariance
Physicists also discuss the time-reversal invariance of local and/or macroscopic descriptions of physical systems, independent of the invariance of the underlying microscopic physical laws.For example, Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
with material absorption
Absorption (electromagnetic radiation)
In physics, absorption of electromagnetic radiation is the way by which the energy of a photon is taken up by matter, typically the electrons of an atom. Thus, the electromagnetic energy is transformed to other forms of energy for example, to heat. The absorption of light during wave propagation is...
or Newtonian mechanics with friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
are not time-reversal invariant at the macroscopic level where they are normally applied, even if they are invariant at the microscopic level when one includes the atomic motions the "lost" energy is translated into.
Macroscopic phenomena: the second law of thermodynamics
Our daily experience shows that T-symmetry does not hold for the behavior of bulk materials. Of these macroscopic laws, most notable is the second law of thermodynamicsSecond law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
. Many other phenomena, such as the relative motion of bodies with friction, or viscous motion of fluids, reduce to this, because the underlying mechanism is the dissipation of usable energy (for example, kinetic energy) into heat.
Is this time-asymmetric dissipation really inevitable? This question has been considered by many physicists, often in the context of Maxwell's demon
Maxwell's demon
In the philosophy of thermal and statistical physics, Maxwell's demon is a thought experiment created by the Scottish physicist James Clerk Maxwell to "show that the Second Law of Thermodynamics has only a statistical certainty." It demonstrates Maxwell's point by hypothetically describing how to...
. The name comes from a thought experiment
Thought experiment
A thought experiment or Gedankenexperiment considers some hypothesis, theory, or principle for the purpose of thinking through its consequences...
described by James Clerk Maxwell
James Clerk Maxwell
James Clerk Maxwell of Glenlair was a Scottish physicist and mathematician. His most prominent achievement was formulating classical electromagnetic theory. This united all previously unrelated observations, experiments and equations of electricity, magnetism and optics into a consistent theory...
in which a microscopic demon guards a gate between two halves of a room. It only lets slow molecules into one half, only fast ones into the other. By eventually making one side of the room cooler than before and the other hotter, it seems to reduce the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of the room, and reverse the arrow of time. Many analyses have been made of this; all show that when the entropy of room and demon are taken together, this total entropy does increase. Modern analyses of this problem have taken into account Claude E. Shannon's relation between entropy and information
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
. Many interesting results in modern computing are closely related to this problem — reversible computing
Reversible computing
Reversible computing is a model of computing where the computational process to some extent is reversible, i.e., time-invertible. A necessary condition for reversibility of a computational model is that the transition function mapping states to their successors at a given later time should be...
, quantum computing and physical limits to computing, are examples. These seemingly metaphysical questions are today, in these ways, slowly being converted to the stuff of the physical sciences.
The current consensus hinges upon the Boltzmann-Shannon identification of the logarithm of phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
volume with the negative of Shannon information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
, and hence to entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
. In this notion, a fixed initial state of a macroscopic system corresponds to relatively low entropy because the coordinates of the molecules of the body are constrained. As the system evolves in the presence of dissipation, the molecular coordinates can move into larger volumes of phase space, becoming more uncertain, and thus leading to increase in entropy.
One can, however equally well imagine a state of the universe in which the motions of all of the particles at one instant were the reverse (strictly, the CPT reverse). Such a state would then evolve in reverse, so presumably entropy would decrease (Loschmidt's paradox
Loschmidt's paradox
Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics...
). Why is 'our' state preferred over the other?
One position is to say that the constant increase of entropy we observe happens only because of the initial state of our universe. Other possible states of the universe (for example, a universe at heat death equilibrium) would actually result in no increase of entropy. In this view, the apparent T-asymmetry of our universe is a problem in cosmology
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
: why did the universe start with a low entropy? This view, if it remains viable in the light of future cosmological observation, would connect this problem to one of the big open questions beyond the reach of today's physics — the question of initial conditions of the universe.
Macroscopic phenomena: black holes
An object can cross through the event horizonEvent horizon
In general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
of a black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
from the outside, and then fall rapidly to the central region where our understanding of physics breaks down. Since within a black hole the forward light-cone is directed towards the center and the backward light-cone is directed outward, it is not even possible to define time-reversal in the usual manner. The only way anything can escape from a black hole is as Hawking radiation
Hawking radiation
Hawking radiation is a thermal radiation with a black body spectrum predicted to be emitted by black holes due to quantum effects. It is named after the physicist Stephen Hawking, who provided a theoretical argument for its existence in 1974, and sometimes also after the physicist Jacob Bekenstein...
.
The time reversal of a black hole would be a hypothetical object known as a white hole
White hole
A white hole, in general relativity, is a hypothetical region of spacetime which cannot be entered from the outside, but from which matter and light may escape. In this sense it is the reverse of a black hole, which can be entered from the outside, but from which nothing, including light, may escape...
. From the outside they appear similar. While a black hole has a beginning and is inescapable, a white hole has an ending and cannot be entered. The forward light-cones of a white hole are directed outward; and its backward light-cones are directed towards the center.
The event horizon of a black hole may be thought of as a surface moving outward at the local speed of light and is just on the edge between escaping and falling back. The event horizon of a white hole is a surface moving inward at the local speed of light and is just on the edge between being swept outward and succeeding in reaching the center. They are two different kinds of horizons—the horizon of a white hole is like the horizon of a black hole turned inside-out.
The modern view of black hole irreveresibility is to relate it to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, since black holes are viewed as thermodynamic objects
Black hole thermodynamics
In physics, black hole thermodynamics is the area of study that seeks to reconcile the laws of thermodynamics with the existence of black hole event horizons...
. Indeed, according to the Gauge-gravity duality conjecture, all microscopic processes in a black hole are reversible, and only the collective behavior is irreversible, as in any other macroscopic, thermal system.
Kinetic consequences: detailed balanceDetailed balanceThe principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
and Onsager reciprocal relationsOnsager reciprocal relationsIn thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists....
In physical and chemical kineticsChemical kinetics
Chemical kinetics, also known as reaction kinetics, is the study of rates of chemical processes. Chemical kinetics includes investigations of how different experimental conditions can influence the speed of a chemical reaction and yield information about the reaction's mechanism and transition...
, T-symmetry of the mechanical microscopic equations implies two important laws: the principle of detailed balance
Detailed balance
The principle of detailed balance is formulated for kinetic systems which are decomposed into elementary processes : At equilibrium, each elementary process should be equilibrated by its reverse process....
and the Onsager reciprocal relations
Onsager reciprocal relations
In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists....
. T-symmetry of the microscopic description together with its kinetic consequences are called microscopic reversibility
Microscopic reversibility
The principle of Microscopic reversibility in physics and chemistry is twofold:* First, it states that the microscopic detailed dynamics of particles and fields is time-reversible because the microscopic equations of motion are symmetric with respect to inversion in time ;* Second, it relates to...
.
Even
Classical variables that do not change upon time reversal include:, Position of a particle in three-space, Acceleration of the particle, Force on the particle, Energy of the particle, Electric potential (voltage), Electric field, Electric displacement, Density of electric charge, Electric polarization
- Energy densityEnergy densityEnergy density is a term used for the amount of energy stored in a given system or region of space per unit volume. Often only the useful or extractable energy is quantified, which is to say that chemically inaccessible energy such as rest mass energy is ignored...
of the electromagnetic field - Maxwell stress tensorMaxwell stress tensorThe Maxwell Stress Tensor is a mathematical object in physics, more precisely it is a second rank tensor used in classical electromagnetism to represent the interaction between electric/magnetic forces and mechanical momentum...
- All masses, charges, coupling constants, and other physical constants, except those associated with the weak force.
Odd
Classical variables that time reversal negates include:, The time when an event occurs, Velocity of a particle, Linear momentum of a particle, Angular momentum of a particle (both orbital and spin), Electromagnetic vector potential, Magnetic induction, Magnetic field, Density of electric current, Magnetization, Poynting vectorPoynting vector
In physics, the Poynting vector can be thought of as representing the directional energy flux density of an electromagnetic field. It is named after its inventor John Henry Poynting. Oliver Heaviside and Nikolay Umov independently co-invented the Poynting vector...
- Power (rate of work done).
Microscopic phenomena: time reversal invariance
Since most systems are asymmetric under time reversal, it is interesting to ask whether there are phenomena that do have this symmetry. In classical mechanics, a velocity v reverses under the operation of T, but an acceleration does not. Therefore, one models dissipative phenomena through terms that are odd inv. However, delicate experiments in which known sources of dissipation are removed reveal that the laws of mechanics are time reversal invariant. Dissipation itself is originated in the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
.
The motion of a charged body in a magnetic field, B involves the velocity through the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
term v×B, and might seem at first to be asymmetric under T. A closer look assures us that B also changes sign under time reversal. This happens because a magnetic field is produced by an electric current, J, which reverses sign under T. Thus, the motion of classical charged particles in electromagnetic field
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
s is also time reversal invariant. (Despite this, it is still useful to consider the time-reversal non-invariance in a local sense when the external field is held fixed, as when the magneto-optic effect
Magneto-optic effect
A magneto-optic effect is any one of a number of phenomena in which an electromagnetic wave propagates through a medium that has been altered by the presence of a quasistatic magnetic field...
is analyzed. This allows one to analyze the conditions under which optical phenomena that locally break time-reversal, such as Faraday isolators, can occur.) The laws of gravity also seem to be time reversal invariant in classical mechanics.
In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
one separates the laws of motion, called kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, from the laws of force, called dynamics
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
. Following the classical kinematics of Newton's laws of motion
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
, the kinematics of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
is built in such a way that it presupposes nothing about the time reversal symmetry of the dynamics. In other words, if the dynamics are invariant, then the kinematics will allow it to remain invariant; if the dynamics is not, then the kinematics will also show this. The structure of the quantum laws of motion are richer, and we examine these next.
Time reversal in quantum mechanics
- that it must be represented as an anti-unitary operator,
- that it protects non-degenerate quantum states from having an electric dipole momentElectric dipole momentIn physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
, - that it has two-dimensional representations with the property T2 = −1.
The strangeness of this result is clear if one compares it with parity. If parity transforms a pair of quantum states into each other, then the sum and difference of these two basis states are states of good parity. Time reversal does not behave like this. It seems to violate the theorem that all abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s be represented by one dimensional irreducible representations. The reason it does this is that it is represented by an anti-unitary operator. It thus opens the way to spinor
Spinor
In mathematics and physics, in particular in the theory of the orthogonal groups , spinors are elements of a complex vector space introduced to expand the notion of spatial vector. Unlike tensors, the space of spinors cannot be built up in a unique and natural way from spatial vectors...
s in quantum mechanics.
Anti-unitary representation of time reversal
Eugene Wigner showed that a symmetry operation S of a Hamiltonian is represented, in quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
either by a unitary operator, S = U, or an antiunitary one, S = UK where U is unitary
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
, and K denotes complex conjugation. These are the only operations that acts on Hilbert space so as to preserve the length of the projection of any one state-vector onto another state-vector.
Consider the parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
operator. Acting on the position, it reverses the directions of space, so that P−1xP = −x. Similarly, it reverses the direction of momentum, so that PpP−1 = −p, where x and p are the position and momentum operators. This preserves the canonical commutator
Canonical commutation relation
In physics, the canonical commutation relation is the relation between canonical conjugate quantities , for example:[x,p_x] = i\hbar...
[x, p] = iħ, where ħ is the reduced Planck constant, only if P is chosen to be unitary, PiP−1 = i.
On the other hand, for time reversal, the time-component of the momentum is the energy. If time reversal were implemented as a unitary operator, it would reverse the sign of the energy just as space-reversal reverses the sign of the momentum. This is not possible, because, unlike momentum, energy is always positive. Since energy in quantum mechanics is defined as the phase factor exp(-iEt) that one gets when one moves forward in time, the way to reverse time while preserving the sign of the energy is to reverse the sense of "i", so that the sense of phases is reversed.
Similarly, any operation that reverses the sense of phase, which changes the sign of i, will turn positive energies into negative energies unless it also changes the direction of time. So every antiunitary symmetry in a theory with positive energy must reverse the direction of time. The only antiunitary symmetry is time reversal, together with a unitary symmetry that does not reverse time.
Given the time reversal operator T, it does nothing to the x-operator, TxT−1 = x, but it reverses the direction of p, so that TpT−1 = −p. The canonical commutator is invariant only if T is chosen to be anti-unitary, i.e., TiT−1 = −i. For a particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
with spin, one can use the representation
where Sy is the y-component of the spin, to find that TJT−1 = −J.
Electric dipole moments
This has an interesting consequence on the electric dipole momentElectric dipole moment
In physics, the electric dipole moment is a measure of the separation of positive and negative electrical charges in a system of charges, that is, a measure of the charge system's overall polarity with SI units of Coulomb-meter...
(EDM) of any particle. The EDM is defined through the shift in the energy of a state when it is put in an external electric field: Δe = d·E + E·δ·E, where d is called the EDM and δ, the induced dipole moment. One important property of an EDM is that the energy shift due to it changes sign under a parity transformation. However, since d is a vector, its expectation value in a state |ψ> must be proportional to <ψ| J |ψ>. Thus, under time reversal, an invariant state must have vanishing EDM. In other words, a non-vanishing EDM signals both P and T symmetry-breaking.
It is interesting to examine this argument further, since one feels that some molecules, such as water, must have EDM irrespective of whether T is a symmetry. This is correct: if a quantum system has degenerate ground states that transform into each other under parity, then time reversal need not be broken to give EDM.
Experimentally observed bounds on the electric dipole moment of the nucleon
Neutron electric dipole moment
The neutron electric dipole moment is a measure for the distribution of positive and negative charge inside the neutron. A finite electric dipole moment can only exist if the centers of the negative and positive charge distribution inside the particle do not coincide. So far, no neutron EDM has...
currently set stringent limits on the violation of time reversal symmetry in the strong interactions, and their modern theory: quantum chromodynamics
Quantum chromodynamics
In theoretical physics, quantum chromodynamics is a theory of the strong interaction , a fundamental force describing the interactions of the quarks and gluons making up hadrons . It is the study of the SU Yang–Mills theory of color-charged fermions...
. Then, using the CPT invariance of a relativistic quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
, this puts strong bounds
CryoEDM
CryoEDM is a particle physics experiment aiming to measure the electric dipole moment of the neutron to a precision of ~10-28ecm. The name is an abbreviation of cryogenic neutron EDM experiment. The previous name nEDM is also sometimes used, but should be avoided where there may be ambiguity...
on strong CP violation.
Experimental bounds on the electron electric dipole moment
Electron electric dipole moment
The electron electric dipole moment de is an intrinsic property of an electron such that the potential energy is linearly related to the strength of the electric field: U=de·E. Within the standard model of elementary particle physics, such a dipole is predicted to be non-zero but very small, at...
also place limits on theories of particle physics and their parameters.
Kramers' theorem
For T, which is an anti-unitary Z2 symmetry generator-
- T2 = UKUK = U U* = U (UT)−1 = Φ,
where Φ is a diagonal matrix of phases. As a result, U = ΦUT and UT = UΦ, showing that
-
- U = Φ U Φ.
This means that the entries in Φ are ±1, as a result of which one may have either T2 = ±1. This is specific to the anti-unitarity of T. For a unitary operator, such as the parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
, any phase is allowed.
Next, take a Hamiltonian invariant under T. Let |a> and T|a> be two quantum states of the same energy. Now, if T2 = −1, then one finds that the states are orthogonal: a result called Kramers' theorem. This implies that if T2 = −1, then there is a twofold degeneracy in the state. This result in non-relativistic quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
presages the spin statistics theorem of quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
.
Quantum states that give unitary representations of time reversal, i.e., have T2=1, are characterized by a multiplicative quantum number
Multiplicative quantum number
In quantum field theory, multiplicative quantum numbers are conserved quantum numbers of a special kind. A given quantum number q is said to be additive if in a particle reaction the sum of the q-values of the interacting particles is the same before and after the reaction. Most conserved quantum...
, sometimes called the T-parity.
Time reversal transformation for fermions in quantum field theories can be represented by an 8-component spinor in which the above mentioned T-parity can be a complex number with unit radius. The CPT invariance is not a theorem but a better to have property in these class of theories.
Time reversal of the known dynamical laws
Particle physicsParticle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
codified the basic laws of dynamics into the standard model
Standard Model
The Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
. This is formulated as a quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
that has CPT symmetry
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
, i.e., the laws are invariant under simultaneous operation of time reversal, parity
Parity (physics)
In physics, a parity transformation is the flip in the sign of one spatial coordinate. In three dimensions, it is also commonly described by the simultaneous flip in the sign of all three spatial coordinates:...
and charge conjugation. However, time reversal itself is seen not to be a symmetry (this is usually called CP violation
CP violation
In particle physics, CP violation is a violation of the postulated CP-symmetry: the combination of C-symmetry and P-symmetry . CP-symmetry states that the laws of physics should be the same if a particle were interchanged with its antiparticle , and left and right were swapped...
). There are two possible origins of this asymmetry, one through the mixing of different flavour
Flavour (particle physics)
In particle physics, flavour or flavor is a quantum number of elementary particles. In quantum chromodynamics, flavour is a global symmetry...
s of quarks in their weak decay
Weak interaction
Weak interaction , is one of the four fundamental forces of nature, alongside the strong nuclear force, electromagnetism, and gravity. It is responsible for the radioactive decay of subatomic particles and initiates the process known as hydrogen fusion in stars...
s, the second through a direct CP violation in strong interactions. The first is seen in experiments, the second is strongly constrained by the non-observation of the EDM of a neutron
Neutron electric dipole moment
The neutron electric dipole moment is a measure for the distribution of positive and negative charge inside the neutron. A finite electric dipole moment can only exist if the centers of the negative and positive charge distribution inside the particle do not coincide. So far, no neutron EDM has...
.
It is important to stress that this time reversal violation is unrelated to the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, because due to the conservation of the CPT symmetry
CPT symmetry
CPT symmetry is a fundamental symmetry of physical laws under transformations that involve the inversions of charge, parity, and time simultaneously.-History:...
, the effect of time reversal is to rename particle
Elementary particle
In particle physics, an elementary particle or fundamental particle is a particle not known to have substructure; that is, it is not known to be made up of smaller particles. If an elementary particle truly has no substructure, then it is one of the basic building blocks of the universe from which...
s as antiparticle
Antiparticle
Corresponding to most kinds of particles, there is an associated antiparticle with the same mass and opposite electric charge. For example, the antiparticle of the electron is the positively charged antielectron, or positron, which is produced naturally in certain types of radioactive decay.The...
s and vice versa. Thus the second law of thermodynamics
Second law of thermodynamics
The second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
is thought to originate in the initial conditions in the universe.
See also
- The second law of thermodynamicsSecond law of thermodynamicsThe second law of thermodynamics is an expression of the tendency that over time, differences in temperature, pressure, and chemical potential equilibrate in an isolated physical system. From the state of thermodynamic equilibrium, the law deduced the principle of the increase of entropy and...
, Maxwell's demonMaxwell's demonIn the philosophy of thermal and statistical physics, Maxwell's demon is a thought experiment created by the Scottish physicist James Clerk Maxwell to "show that the Second Law of Thermodynamics has only a statistical certainty." It demonstrates Maxwell's point by hypothetically describing how to...
and the arrow of timeArrow of timeThe arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
(also Loschmidt's paradoxLoschmidt's paradoxLoschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics...
). - Applications to reversible computingReversible computingReversible computing is a model of computing where the computational process to some extent is reversible, i.e., time-invertible. A necessary condition for reversibility of a computational model is that the transition function mapping states to their successors at a given later time should be...
and quantum computing, including limits to computing. - The standard modelStandard ModelThe Standard Model of particle physics is a theory concerning the electromagnetic, weak, and strong nuclear interactions, which mediate the dynamics of the known subatomic particles. Developed throughout the mid to late 20th century, the current formulation was finalized in the mid 1970s upon...
of particle physics, CP violationCP violationIn particle physics, CP violation is a violation of the postulated CP-symmetry: the combination of C-symmetry and P-symmetry . CP-symmetry states that the laws of physics should be the same if a particle were interchanged with its antiparticle , and left and right were swapped...
, the CKM matrix and the strong CP problem - Neutrino masses and CPT invariance.
- Wheeler–Feynman absorber theory
- TeleonomyTeleonomyTeleonomy is the quality of apparent purposefulness and of goal-directedness of structures and functions in living organisms that derive from their evolutionary history, adaptation for reproductive success, or generally, due to the operation of a program....