
Killing vector field
Encyclopedia
In mathematics
, a Killing vector field (often just Killing field) , named after Wilhelm Killing
, is a vector field
on a Riemannian manifold
(or pseudo-Riemannian manifold
) that preserves the metric
. Killing fields are the infinitesimal generators of isometries
; that is, flows generated by Killing fields are continuous isometries
of the manifold
. More simply, the flow generates a symmetry
, in the sense that moving each point on an object the same distance in the direction of the Killing vector field will not distort distances on the object.
with respect to X of the metric g vanishes:

In terms of the Levi-Civita connection
, this is
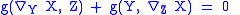
for all vectors Y and Z. In local coordinates
, this amounts to the Killing equation
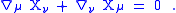
This condition is expressed in covariant form. Therefore it is sufficient to establish it in a preferred coordinate system in order to have it hold in all coordinate systems.
s of the field at the point).
The Lie bracket
of two Killing fields is still a Killing field. The Killing fields on a manifold M thus form a Lie subalgebra
of vector fields on M. This is the Lie algebra of the isometry group
of the manifold if M is complete.
For compact
manifolds

for some scalar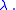 The derivatives of one parameter families of conformal map
The derivatives of one parameter families of conformal map
s are conformal Killing fields.
Another generalization is to conformal Killing tensor fields. These are symmetric tensor
fields T such that the trace-free part of the symmetrization of vanishes.
vanishes.
Killing vector fields can also be defined on any (possibly nonmetric) manifold M if we take any Lie group G acting
on it instead of the group of isometries. In this broader sense, a Killing vector field is the pushforward of a left invariant vector field on G by the group action. If the group action is effective, then the space of the Killing vector fields is isomorphic to the Lie algebra of G.
of G.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Killing vector field (often just Killing field) , named after Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
, is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
on a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
(or pseudo-Riemannian manifold
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
) that preserves the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
. Killing fields are the infinitesimal generators of isometries
Isometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
; that is, flows generated by Killing fields are continuous isometries
Isometry (Riemannian geometry)
In the study of Riemannian geometry in mathematics, a local isometry from one Riemannian manifold to another is a map which pulls back the metric tensor on the second manifold to the metric tensor on the first...
of the manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
. More simply, the flow generates a symmetry
Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
, in the sense that moving each point on an object the same distance in the direction of the Killing vector field will not distort distances on the object.
Explanation
Specifically, a vector field X is a Killing field if the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
with respect to X of the metric g vanishes:

In terms of the Levi-Civita connection
Levi-Civita connection
In Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
, this is
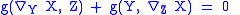
for all vectors Y and Z. In local coordinates
Local coordinates
Local coordinates are measurement indices into a local coordinate system or a local coordinate space. A simple example is using house numbers to locate a house on a street; the street is a local coordinate system within a larger system composed of city townships, states, countries, etc.Local...
, this amounts to the Killing equation
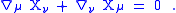
This condition is expressed in covariant form. Therefore it is sufficient to establish it in a preferred coordinate system in order to have it hold in all coordinate systems.
Examples
- The vector field on a circle that points clockwise and has the same length at each point is a Killing vector field, since moving each point on the circle along this vector field simply rotates the circle.
- If the metric coefficients
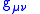 in some coordinate basis
in some coordinate basis 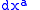 are independent of
are independent of 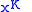 , then
, then  is automatically a Killing vector, where
is automatically a Killing vector, where  is the Kronecker delta. (Misner, et al., 1973).
is the Kronecker delta. (Misner, et al., 1973).
To prove this, let us assume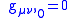
Then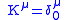 and
and 
Now let us look at the Killing condition
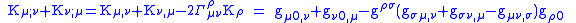
and from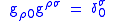
The Killing condition becomes
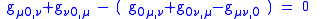
- The physical meaning is, for example, that, if none of the metric coefficients is a function of time, the manifold must automatically have a time-like Killing vector.
- In layman's terms, if an object doesn't transform or "evolve" in time (when time passes), time passing won't change the measures of the object. Formulated like this, the result sounds like a tautology, but one has to understand that the example is very much contrived: Killing fields apply also to much more complex and interesting cases.
Properties of Killing fields
A Killing field is determined uniquely by a vector at some point and its gradient (i.e. all covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
s of the field at the point).
The Lie bracket
Lie bracket of vector fields
In the mathematical field of differential topology, the Lie bracket of vector fields, Jacobi–Lie bracket, or commutator of vector fields is a bilinear differential operator which assigns, to any two vector fields X and Y on a smooth manifold M, a third vector field denoted [X, Y]...
of two Killing fields is still a Killing field. The Killing fields on a manifold M thus form a Lie subalgebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
of vector fields on M. This is the Lie algebra of the isometry group
Isometry group
In mathematics, the isometry group of a metric space is the set of all isometries from the metric space onto itself, with the function composition as group operation...
of the manifold if M is complete.
For compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
manifolds
- Negative Ricci curvatureRicci curvatureIn differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
implies there are no nontrivial (nonzero) Killing fields. - Nonpositive Ricci curvatureRicci curvatureIn differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
implies that any Killing field is parallel. i.e. covariant derivative along any vector j field is identically zero. - If the sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
is positive and the dimension of M is even, a Killing field must have a zero.
Generalizations
Killing vector fields can be generalized to conformal Killing vector fields defined by
for some scalar
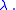 The derivatives of one parameter families of conformal map
The derivatives of one parameter families of conformal mapConformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
s are conformal Killing fields.
Another generalization is to conformal Killing tensor fields. These are symmetric tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
fields T such that the trace-free part of the symmetrization of
 vanishes.
vanishes.Killing vector fields can also be defined on any (possibly nonmetric) manifold M if we take any Lie group G acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on it instead of the group of isometries. In this broader sense, a Killing vector field is the pushforward of a left invariant vector field on G by the group action. If the group action is effective, then the space of the Killing vector fields is isomorphic to the Lie algebra
 of G.
of G.See also
- Affine vector fieldAffine vector fieldAn affine vector field is a projective vector field preserving geodesics and preserving the affine parameter...
- Curvature collineation
- Homothetic vector field
- Killing formKilling formIn mathematics, the Killing form, named after Wilhelm Killing, is a symmetric bilinear form that plays a basic role in the theories of Lie groups and Lie algebras...
- Killing horizonKilling horizonA Killing horizon is a null hypersurface on which there is a null Killing vector field .Associated to a Killing horizon is a geometrical quantity known as surface gravity, \kappa...
- Killing spinorKilling spinorKilling spinor is a term used in mathematics and physics. By the more narrow definition, commonly used in mathematics, the term Killing spinor indicates those twistorspinors which are also eigenspinors of the Dirac operator, see Th. Friedrich ,...
- Killing tensor
- Matter collineation
- Spacetime symmetriesSpacetime symmetriesSpacetime symmetries are features of spacetime that can be described as exhibiting some form of symmetry. The role of symmetry in physics is important in simplifying solutions to many problems, spacetime symmetries finding ample application in the study of exact solutions of Einstein's field...

