
G-parity
Encyclopedia
In theoretical physics
, G-parity is a multiplicative quantum number
that results from the generalization of C-parity to multiplet
s of particles.
C-parity applies only to neutral systems; in the pion
triplet, only π0 has C-parity. On the other hand, strong interaction
does not see electrical charge, so it cannot distinguish amongst π+, π0 and π−. We can generalize the C-parity so it applies to all charge states of a given multiplet: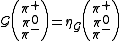
where ηG = ±1 are the eigenvalues of G-parity. The G-parity operator is defined as
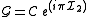
where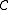 is the C-parity operator, and I2 is the operator associated with the 2nd component of the isospin
is the C-parity operator, and I2 is the operator associated with the 2nd component of the isospin
"vector". G-parity is a combination of charge conjugation and a π
rad
(180°) rotation around the 2nd axis of isospin space. Given that charge conjugation and isospin are preserved by strong interactions, so is G. Weak and electromagnetic interactions, though, are not invariant under G-parity.
Since G-parity is applied on a whole multiplet, charge conjugation has to see the multiplet as a neutral entity. Thus, only multiplets with an average charge of 0 will be eigenstates of G, that is
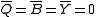
(see Q, B, Y
).
In general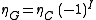
where ηC is a C-parity eigenvalue, and I is the isospin. For fermion-antifermion
systems, we have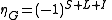 .
.
where S is the total spin
, L the total orbital angular momentum quantum number. For boson–antiboson
systems we have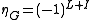 .
.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, G-parity is a multiplicative quantum number
Multiplicative quantum number
In quantum field theory, multiplicative quantum numbers are conserved quantum numbers of a special kind. A given quantum number q is said to be additive if in a particle reaction the sum of the q-values of the interacting particles is the same before and after the reaction. Most conserved quantum...
that results from the generalization of C-parity to multiplet
Multiplet
In group theory, a multiplet is formally a group representation of an algebra.In physics, multiplet can mean:* A group of related spectral lines* A group of related subatomic particles...
s of particles.
C-parity applies only to neutral systems; in the pion
Pion
In particle physics, a pion is any of three subatomic particles: , , and . Pions are the lightest mesons and they play an important role in explaining the low-energy properties of the strong nuclear force....
triplet, only π0 has C-parity. On the other hand, strong interaction
Strong interaction
In particle physics, the strong interaction is one of the four fundamental interactions of nature, the others being electromagnetism, the weak interaction and gravitation. As with the other fundamental interactions, it is a non-contact force...
does not see electrical charge, so it cannot distinguish amongst π+, π0 and π−. We can generalize the C-parity so it applies to all charge states of a given multiplet:
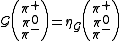
where ηG = ±1 are the eigenvalues of G-parity. The G-parity operator is defined as
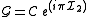
where
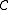 is the C-parity operator, and I2 is the operator associated with the 2nd component of the isospin
is the C-parity operator, and I2 is the operator associated with the 2nd component of the isospinIsospin
In physics, and specifically, particle physics, isospin is a quantum number related to the strong interaction. This term was derived from isotopic spin, but the term is confusing as two isotopes of a nucleus have different numbers of nucleons; in contrast, rotations of isospin maintain the number...
"vector". G-parity is a combination of charge conjugation and a π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
rad
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
(180°) rotation around the 2nd axis of isospin space. Given that charge conjugation and isospin are preserved by strong interactions, so is G. Weak and electromagnetic interactions, though, are not invariant under G-parity.
Since G-parity is applied on a whole multiplet, charge conjugation has to see the multiplet as a neutral entity. Thus, only multiplets with an average charge of 0 will be eigenstates of G, that is
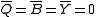
(see Q, B, Y
Hypercharge
In particle physics, the hypercharge Y of a particle is related to the strong interaction, and is distinct from the similarly named weak hypercharge, which has an analogous role in the electroweak interaction...
).
In general
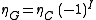
where ηC is a C-parity eigenvalue, and I is the isospin. For fermion-antifermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
systems, we have
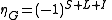 .
.where S is the total spin
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
, L the total orbital angular momentum quantum number. For boson–antiboson
Boson
In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose....
systems we have
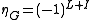 .
.

