
Link (knot theory)
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a link is a collection of knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
s which do not intersect, but which may be linked (or knotted) together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
. Implicit in this definition is that there is a trivial reference link, usually called the unlink
Unlink
In the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...
, but the word is also sometimes used in context where there is no notion of a trivial link.

Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(or often the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
) whose connected component
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
s are homeomorphic to circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s.
The simplest nontrivial example of a link with more than one component is called the Hopf link
Hopf link
thumb|right|[[Skein relation]] for the Hopf link.In mathematical knot theory, the Hopf link, named after Heinz Hopf, is the simplest nontrivial link with more than one component. It consists of two circles linked together exactly once...
, which consists of two circles (or unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
s) linked together once. The circles in
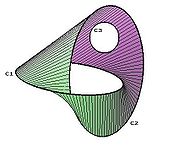
the Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
are collectively linked despite the fact that no two of them are directly linked. The Borromean rings thus form a Brunnian link
Brunnian link
In knot theory, a branch of mathematics, a Brunnian link is a nontrivial link that becomes trivial if any component is removed. In other words, cutting any loop frees all the other loops ....
and in fact constitute the simplest such link.

General manifolds
Frequently the word link is used to describe any submanifold of the sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
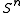 diffeomorphic to a disjoint union of a finite number of sphere
diffeomorphic to a disjoint union of a finite number of sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s,
 .
.In full generality, the word link is essentially the same as the word knot – the context is that one has a submanifold M of a manifold N (considered to be trivially embedded) and a non-trivial embedding of M in N, non-trivial in the sense that the 2nd embedding is not isotopic
Ambient isotopy
In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...
to the 1st. If M is disconnected, the embedding is called a link (or said to be linked). If M is connected, it is called a knot.
Tangles, string links, and braids
While (1-dimensional) links are defined as embeddings of circles, it is often interesting and especially technically useful to consider embedded intervals (strands), as in braid theoryBraid theory
In topology, a branch of mathematics, braid theory is an abstract geometric theory studying the everyday braid concept, and some generalizations. The idea is that braids can be organized into groups, in which the group operation is 'do the first braid on a set of strings, and then follow it with a...
.
Most generally, one can consider a tangle – a tangle is an embedding
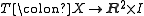
of a (smooth) compact 1-manifold with boundary
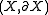 into the plane times the interval
into the plane times the interval 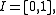 such that the boundary
such that the boundary 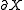 is embedded in
is embedded in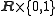 (
( ).
).The type of a tangle is the manifold X, together with a fixed embedding of
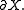
Concretely, a connected compact 1-manifold with boundary is an interval
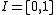 or a circle
or a circle 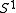 (compactness rules out the open interval
(compactness rules out the open interval 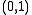 and the half-open interval
and the half-open interval 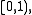 neither of which yields non-trivial embeddings since the open end means that they can be shrunk to a point), so a possibly disconnected compact 1-manifold is a collection of n intervals
neither of which yields non-trivial embeddings since the open end means that they can be shrunk to a point), so a possibly disconnected compact 1-manifold is a collection of n intervals 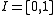 and m circles
and m circles 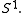 The condition that the boundary of X lies in
The condition that the boundary of X lies in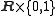
says that intervals either connect two lines or connect two points on one of the lines, but imposes no conditions on the circles.
One may view tangles as having a vertical direction (I), lying between and possibly connecting two lines,
and then being able to move in a two-dimensional horizontal direction (
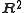 )
)between these lines; one can project these to form a tangle diagram, analogous to a knot diagram.
Tangles include links (if X consists of circles only), braids, and others besides – for example, a strand connecting the two lines together with a circle linked around it.
In this context, a braid is defined as a tangle which is always going down – whose derivative always has a non-zero component in the vertical (I) direction. In particular, it must consist solely of intervals, and not double back on itself; however, no specification is made on where on the line the ends lie.
A string link is a tangle consisting of only intervals, with the ends of each strand required to lie at (0, 0), (0, 1), (1, 0), (1, 1), (2, 0), (2, 1), ... – i.e., connecting the integers, and ending in the same order that they began (one may use any other fixed set of points); if this has ℓ components, we call it an "ℓ-component string link". A string link need not be a braid – it may double back on itself, such as a two-component string link that features an overhand knot
Overhand knot
The overhand knot is one of the most fundamental knots and forms the basis of many others including the simple noose, overhand loop, angler's loop, reef knot, fisherman's knot and water knot. The overhand knot is very secure, to the point of jamming badly. It should be used if the knot is...
. A braid that is also a string link is called a pure braid, and corresponds with the usual such notion.
The key technical value of tangles and string links is that they have algebraic structure. Isotopy classes of tangles form a tensor category, where for the category structure, one can compose two tangles if the bottom end of one equals the top end of the other (so the boundaries can be stitched together), by stacking them – they do not literally form a category (pointwise) because there is no identity, since even a trivial tangle takes up vertical space, but up to isotopy they do. The tensor structure is given by juxtaposition of tangles – putting one tangle to the right of the other.
For a fixed ℓ, isotopy classes of ℓ-component string links form a monoid (one can compose all ℓ-component string links, and there is an identity), but not a group, as isotopy classes of string links need not have inverses. However, concordance classes (and thus also homotopy classes) of string links do have inverses, where inverse is given by flipping the string link upside down, and thus form a group.
Every link can be cut apart to form a string link, though this is not unique, and invariants of links can sometimes be understood as invariants of string links – this is the case for Milnor's invariants, for instance. Compare with closed braids.

