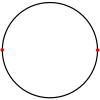
Digon - AbsoluteAstronomy.com

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

, a digon is a polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

with two sides (edges) and two vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

. It is degenerate

Degeneracy (mathematics)

In mathematics, a degenerate case is a limiting case in which a class of object changes its nature so as to belong to another, usually simpler, class....

in a Euclidean space

Euclidean geometry

Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...

, but may be non-degenerate in a spherical space

Spherical geometry

Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....

.

A digon must be regular

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

because its two edges are the same length. It has Schläfli symbol {2}.

Some authorities do not consider the digon to be a proper polygon because of its degeneracy in the Euclidean case, but most formulae on general polygons do work on the digon. For example, the angle sum of an n-gon,

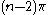, would become 0 when n = 2, which is correct for a Euclidean digon.

In spherical tilings

In Euclidean geometry

Euclidean geometry

a digon is always degenerate. However, in spherical geometry

Spherical geometry

a nondegenerate digon (with a nonzero interior area) can exist if the vertices are antipodal

Antipodal point

In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....

. The internal angle

Internal angle

In geometry, an interior angle is an angle formed by two sides of a polygon that share an endpoint. For a simple, convex or concave polygon, this angle will be an angle on the 'inner side' of the polygon...

of the spherical digon vertex can be any angle between 0 and 180 degrees. Such a spherical polygon can also be called a lune

Lune (mathematics)

In geometry, a lune is either of two figures, both shaped roughly like a crescent Moon. The word "lune" derives from luna, the Latin word for Moon.-Plane geometry:...

In polyhedra

A digon is considered a degenerate face

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

of a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

because it has no geometric area and edges are overlapping. But sometimes it can have a useful topological existence in transforming polyhedra.

Any polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

can be topologically modified by replacing an edge with a digon. Such an operation adds one edge and one face to the polyhedron, although the result is geometrically identical. This transformation has no effect on the Euler characteristic

Euler characteristic

In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...

(χ=V-E+F).

A digon face can also be created by geometrically collapsing a quadrilateral

Quadrilateral

In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...

face by moving pairs of vertices to coincide in space. This digon can then be replaced by a single edge. It loses one face, two vertices, and three edges, again leaving the Euler characteristic

Euler characteristic

unchanged.

Classes of polyhedra can be derived as degenerate forms of a primary polyhedron, with faces sometimes being degenerated into coinciding vertices. For example, this class of 7 uniform polyhedron

Uniform polyhedron

A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...

with octahedral symmetry

Octahedral symmetry

150px|thumb|right|The [[cube]] is the most common shape with octahedral symmetryA regular octahedron has 24 rotational symmetries, and a symmetry order of 48 including transformations that combine a reflection and a rotation...

exist as degenerate forms of the truncated cuboctahedron

Truncated cuboctahedron

In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...

(4.6.8). This principle is used in the Wythoff construction

Wythoff construction

In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...

4.4.4 Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...	3.8.8 Truncated cube In geometry, the truncated cube, or truncated hexahedron, is an Archimedean solid. It has 14 regular faces , 36 edges, and 24 vertices....	3.4.3.4 Cuboctahedron In geometry, a cuboctahedron is a polyhedron with eight triangular faces and six square faces. A cuboctahedron has 12 identical vertices, with two triangles and two squares meeting at each, and 24 identical edges, each separating a triangle from a square. As such it is a quasiregular polyhedron,...	4.6.6 Truncated octahedron In geometry, the truncated octahedron is an Archimedean solid. It has 14 faces , 36 edges, and 24 vertices. Since each of its faces has point symmetry the truncated octahedron is a zonohedron....	3.3.3.3 Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....	3.4.4.4 Rhombicuboctahedron In geometry, the rhombicuboctahedron, or small rhombicuboctahedron, is an Archimedean solid with eight triangular and eighteen square faces. There are 24 identical vertices, with one triangle and three squares meeting at each. Note that six of the squares only share vertices with the triangles...	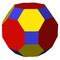4.6.8 Truncated cuboctahedron In geometry, the truncated cuboctahedron is an Archimedean solid. It has 12 square faces, 8 regular hexagonal faces, 6 regular octagonal faces, 48 vertices and 72 edges...

In spherical tilings

In polyhedra

See also