Crossing number (knot theory)
Encyclopedia
In the mathematical
area of knot theory
, the crossing number of a knot
is the minimal number of crossings of any diagram of the knot. It is a knot invariant
.
By way of example, the unknot
has crossing number zero
, the trefoil knot
three and the figure-eight knot
four. There are no other knots with a crossing number this low, and just two knots have crossing number five, but the number of knots with a particular crossing number increases rapidly as the crossing number increases.
Tables of prime knot
s are traditionally indexed by crossing number, with a subscript to indicate which particular knot out of those with this many crossings is meant (this sub-ordering is not based on anything in particular, except that torus knot
s are listed first). The listing goes 31 (the trefoil knot), 41 (the figure-eight knot), 51, 52, 61, etc. This order has not changed significantly since P. G. Tait published a tabulation of knots in 1877.
There has been very little progress on understanding the behavior of crossing number under rudimentary operations on knots. A big open question asks if the crossing number is additive when taking knot sums. It is also expected that a satellite
of a knot K should have larger crossing number than K, but this has not been proven.
Additivity of crossing number under knot sum has been proven for special cases, for example if the summands are alternating knot
s (or more generally, adequate knot), or if the summands are torus knot
s. Marc Lackenby has also given a proof that there is a constant N > 1 such that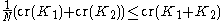
, but his method, which utilizes normal surface
s, cannot improve N to 1.
There are related concepts of average crossing number
and asymptotic crossing number. Both of these quantities bound the standard crossing number. Asymptotic crossing number is conjectured to be equal to crossing number.
There are mysterious connections between the crossing number of a knot and the physical behavior of DNA
knots. For prime DNA knots, crossing number is a good predictor of the relative velocity of the DNA knot in agarose gel electrophoresis
. Basically, the higher the crossing number, the faster the relative velocity. For composite knots, this does not appear to be the case, although experimental conditions can drastically change the results.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
area of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the crossing number of a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is the minimal number of crossings of any diagram of the knot. It is a knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
.
By way of example, the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
has crossing number zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
, the trefoil knot
Trefoil knot
In topology, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop...
three and the figure-eight knot
Figure-eight knot (mathematics)
In knot theory, a figure-eight knot is the unique knot with a crossing number of four. This is the smallest possible crossing number except for the unknot and trefoil knot...
four. There are no other knots with a crossing number this low, and just two knots have crossing number five, but the number of knots with a particular crossing number increases rapidly as the crossing number increases.
Tables of prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
s are traditionally indexed by crossing number, with a subscript to indicate which particular knot out of those with this many crossings is meant (this sub-ordering is not based on anything in particular, except that torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
s are listed first). The listing goes 31 (the trefoil knot), 41 (the figure-eight knot), 51, 52, 61, etc. This order has not changed significantly since P. G. Tait published a tabulation of knots in 1877.
There has been very little progress on understanding the behavior of crossing number under rudimentary operations on knots. A big open question asks if the crossing number is additive when taking knot sums. It is also expected that a satellite
Satellite knot
In the mathematical theory of knots, a satellite knot is a knot that contains an incompressible, non-boundary parallel torus in its complement. The class of satellite knots include composite knots, cable knots and Whitehead doubles. A satellite knot K can be picturesquely described as follows:...
of a knot K should have larger crossing number than K, but this has not been proven.
Additivity of crossing number under knot sum has been proven for special cases, for example if the summands are alternating knot
Alternating knot
In knot theory, a link diagram is alternating if the crossings alternate under, over, under, over, as you travel along each component of the link. A link is alternating if it has an alternating diagram....
s (or more generally, adequate knot), or if the summands are torus knot
Torus knot
In knot theory, a torus knot is a special kind of knot that lies on the surface of an unknotted torus in R3. Similarly, a torus link is a link which lies on the surface of a torus in the same way. Each torus knot is specified by a pair of coprime integers p and q. A torus link arises if p and q...
s. Marc Lackenby has also given a proof that there is a constant N > 1 such that
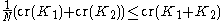, but his method, which utilizes normal surfaceNormal surface
In mathematics, a normal surface is a surface inside a triangulated 3-manifold that intersects each tetrahedron so that each component of intersection is a triangle or a quad . A triangle cuts off a vertex of the tetrahedron while a quad separates pairs of vertices...
s, cannot improve N to 1.
There are related concepts of average crossing number
Average crossing number
In the mathematical subject of knot theory, the average crossing number of a knot is the result of averaging over all directions the number of crossings in a knot diagram of the knot obtained by projection onto the plane orthogonal to the direction...
and asymptotic crossing number. Both of these quantities bound the standard crossing number. Asymptotic crossing number is conjectured to be equal to crossing number.
There are mysterious connections between the crossing number of a knot and the physical behavior of DNA
DNA
Deoxyribonucleic acid is a nucleic acid that contains the genetic instructions used in the development and functioning of all known living organisms . The DNA segments that carry this genetic information are called genes, but other DNA sequences have structural purposes, or are involved in...
knots. For prime DNA knots, crossing number is a good predictor of the relative velocity of the DNA knot in agarose gel electrophoresis
Gel electrophoresis
Gel electrophoresis is a method used in clinical chemistry to separate proteins by charge and or size and in biochemistry and molecular biology to separate a mixed population of DNA and RNA fragments by length, to estimate the size of DNA and RNA fragments or to separate proteins by charge...
. Basically, the higher the crossing number, the faster the relative velocity. For composite knots, this does not appear to be the case, although experimental conditions can drastically change the results.
Other numerical knot invariants
- Bridge numberBridge numberIn a mathematical field of knot theory, the bridge number is an invariant of a knot. It is defined as the minimal number of bridges required in all the possible bridge representations of a knot...
- Linking coefficient
- Unknotting numberUnknotting numberIn the mathematical area of knot theory, the unknotting number of a knot is the minimum number of times the knot must be passed through itself to untie it. If a knot has unknotting number n, then there exists a diagram of the knot which can be changed to unknot by switching n crossings...
- Stick numberStick numberIn the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot...
Further reading
- Gruber, H. Estimates for the minimal crossing number. arXiv:math/0303273v3 (math.GT), 2003