
Hopf link
Encyclopedia
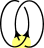
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the Hopf link, named after Heinz Hopf
Heinz Hopf
Heinz Hopf was a German mathematician born in Gräbschen, Germany . He attended Dr. Karl Mittelhaus' higher boys' school from 1901 to 1904, and then entered the König-Wilhelm- Gymnasium in Breslau. He showed mathematical talent from an early age...
, is the simplest nontrivial link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
with more than one component. It consists of two circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s linked together exactly once. For a concrete model, take the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
in the xy-plane centered at the origin and another unit circle in the yz-plane centered at (0,1,0).
Depending on the relative orientation
Orientation (geometry)
In geometry the orientation, angular position, or attitude of an object such as a line, plane or rigid body is part of the description of how it is placed in the space it is in....
s of the two components the linking number
Linking number
In mathematics, the linking number is a numerical invariant that describes the linking of two closed curves in three-dimensional space. Intuitively, the linking number represents the number of times that each curve winds around the other...
of the Hopf link is ±1.
The Hopf link is a (2,2)-torus link with the braid word
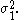
In the Hopf bundle
Hopf bundle
In the mathematical field of topology, the Hopf fibration describes a 3-sphere in terms of circles and an ordinary sphere. Discovered by Heinz Hopf in 1931, it is an influential early example of a fiber bundle...
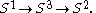
The fibers over any two distinct points in S2 form a Hopf link in the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
S3.
External links
- The Hopf Link at the wiki Knot Atlas.

