
Knot invariant
Encyclopedia
In the mathematical
field of knot theory
, a knot invariant is a quantity (in a broad sense) defined for each knot
which is the same for equivalent knots. The equivalence is often given by ambient isotopy
but can be given by homeomorphism
. Some invariants are indeed numbers, but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory
. Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics.
From the modern perspective, it is natural to define a knot invariant from a knot diagram. Of course, it must be unchanged (that is to say, invariant) under the Reidemeister moves. Tricolorability
is a particularly simple example. Other examples are knot polynomial
s, such as the Jones polynomial, which are currently among the most useful invariants for distinguishing knots from one another, though at the time of writing it is not known whether there exists a knot polynomial which distinguishes all knots from each other, or even which distinguishes just the unknot
from all other knots.
Other invariants can be defined by considering some integer-valued function of knot diagrams and taking its minimum value over all possible diagrams of a given knot. This category includes the crossing number
, which is the minimum number of crossings for any diagram of the knot, and the bridge number
, which is the minimum number of bridges for any diagram of the knot.
Historically, many of the early knot invariants are not defined by first selecting a diagram but defined intrinsically, which can make computing some of these invariants a challenge. For example, knot genus is particularly tricky to compute, but can be effective (for instance, in distinguishing mutants
).
The complement of a knot
itself (as a topological space
) is known to be a "complete invariant" of the knot by the Gordon–Luecke theorem in the sense that it distinguishes the given knot from all other knots up to ambient isotopy
and mirror image. Some invariants associated with the knot complement include the knot group
which is just the fundamental group
of the complement. The knot quandle is also a complete invariant in this sense but it is difficult to determine if two quandles are isomorphic.
By Mostow–Prasad rigidity
, the hyperbolic structure on the complement of a hyperbolic link
is unique, which means the hyperbolic volume
is an invariant for these knots and links. Volume, and other hyperbolic invariants, have proven very effective, utilized in some of the extensive efforts at knot tabulation.
In recent years, there has been much interest in homological
invariants of knots which categorify
well-known invariants. Heegaard Floer homology is a homology theory
whose Euler characteristic
is the Alexander polynomial
of the knot. It has been proven effective in deducing new results about the classical invariants. Along a different line of study, there is a combinatorially defined cohomology theory of knots called Khovanov homology
whose Euler characteristic is the Jones polynomial. This has recently been shown to be useful in obtaining bounds on slice genus
whose earlier proofs required gauge theory
. Khovanov
and Rozansky have since defined several other related cohomology theories whose Euler characteristics recover other classical invariants. Stroppel gave a representation theoretic interpretation of Khovanov homology by categorifying quantum group invariants.
There is also growing interest from both knot theorists and scientists in understanding "physical" or geometric properties of knots and relating it to topological invariants and knot type. An old result in this direction is the Fary–Milnor theorem states that if the total curvature
of a knot K in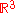 satisfies
satisfies

where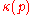 is the curvature at p, then K is an unknot. Therefore, for knotted curves,
is the curvature at p, then K is an unknot. Therefore, for knotted curves,
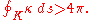
An example of a "physical" invariant is ropelength
, which is the amount of 1-inch diameter rope needed to realize a particular knot type.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, a knot invariant is a quantity (in a broad sense) defined for each knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
which is the same for equivalent knots. The equivalence is often given by ambient isotopy
Ambient isotopy
In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...
but can be given by homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
. Some invariants are indeed numbers, but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
. Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics.
From the modern perspective, it is natural to define a knot invariant from a knot diagram. Of course, it must be unchanged (that is to say, invariant) under the Reidemeister moves. Tricolorability
Tricolorability
In the mathematical field of knot theory, the tricolorability of a knot is the ability of a knot to be colored with three colors subject to certain rules. Tricolorability is an isotopy invariant, and hence can be used to distinguish between two different knots...
is a particularly simple example. Other examples are knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
s, such as the Jones polynomial, which are currently among the most useful invariants for distinguishing knots from one another, though at the time of writing it is not known whether there exists a knot polynomial which distinguishes all knots from each other, or even which distinguishes just the unknot
Unknot
The unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
from all other knots.
Other invariants can be defined by considering some integer-valued function of knot diagrams and taking its minimum value over all possible diagrams of a given knot. This category includes the crossing number
Crossing number (knot theory)
In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....
, which is the minimum number of crossings for any diagram of the knot, and the bridge number
Bridge number
In a mathematical field of knot theory, the bridge number is an invariant of a knot. It is defined as the minimal number of bridges required in all the possible bridge representations of a knot...
, which is the minimum number of bridges for any diagram of the knot.
Historically, many of the early knot invariants are not defined by first selecting a diagram but defined intrinsically, which can make computing some of these invariants a challenge. For example, knot genus is particularly tricky to compute, but can be effective (for instance, in distinguishing mutants
Mutation (knot theory)
In the mathematical field of knot theory, a mutation is an operation on a knot that can produce different knots. Suppose K is a knot given in the form of a knot diagram. Consider a disc D in the projection plane of the diagram whose boundary circle intersects K exactly four times...
).
The complement of a knot
Knot complement
In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...
itself (as a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
) is known to be a "complete invariant" of the knot by the Gordon–Luecke theorem in the sense that it distinguishes the given knot from all other knots up to ambient isotopy
Ambient isotopy
In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...
and mirror image. Some invariants associated with the knot complement include the knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
which is just the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the complement. The knot quandle is also a complete invariant in this sense but it is difficult to determine if two quandles are isomorphic.
By Mostow–Prasad rigidity
Mostow rigidity theorem
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
, the hyperbolic structure on the complement of a hyperbolic link
Hyperbolic link
In mathematics, a hyperbolic link is a link in the 3-sphere with complement that has a complete Riemannian metric of constant negative curvature, i.e. has a hyperbolic geometry...
is unique, which means the hyperbolic volume
Hyperbolic volume (knot)
In the mathematical field of knot theory, the hyperbolic volume of a hyperbolic link is simply the volume of the link's complement with respect to its complete hyperbolic metric. The volume is necessarily finite. The hyperbolic volume of a non-hyperbolic knot is often defined to be zero...
is an invariant for these knots and links. Volume, and other hyperbolic invariants, have proven very effective, utilized in some of the extensive efforts at knot tabulation.
In recent years, there has been much interest in homological
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
invariants of knots which categorify
Categorification
In mathematics, categorification refers to the process of replacing set-theoretic theorems by category-theoretic analogues. Categorification, when done successfully, replaces sets by categories, functions with functors, and equations by natural isomorphisms of functors satisfying additional...
well-known invariants. Heegaard Floer homology is a homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
whose Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
is the Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of the knot. It has been proven effective in deducing new results about the classical invariants. Along a different line of study, there is a combinatorially defined cohomology theory of knots called Khovanov homology
Khovanov homology
In mathematics, Khovanov homology is an invariant of oriented knots and links that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial....
whose Euler characteristic is the Jones polynomial. This has recently been shown to be useful in obtaining bounds on slice genus
Slice genus
In mathematics, the slice genus of a smooth knot K in S3 is the least integer g such that K is the boundary of a connected, orientable 2-manifold S of genus g embedded in the 4-ball D4 bounded by S3.More precisely, if S is required to be smoothly embedded, then this integer g is the...
whose earlier proofs required gauge theory
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
. Khovanov
Mikhail Khovanov
Mikhail Khovanov is a professor of mathematics at Columbia University. He earned a PhD in mathematics from Yale University in 1997, where he studied under Igor Frenkel. His interests include knot theory and algebraic topology...
and Rozansky have since defined several other related cohomology theories whose Euler characteristics recover other classical invariants. Stroppel gave a representation theoretic interpretation of Khovanov homology by categorifying quantum group invariants.
There is also growing interest from both knot theorists and scientists in understanding "physical" or geometric properties of knots and relating it to topological invariants and knot type. An old result in this direction is the Fary–Milnor theorem states that if the total curvature
Total curvature
In mathematical study of the differential geometry of curves, the total curvature of an immersed plane curve is the integral of curvature along a curve taken with respect to arclength:\int_a^b k\,ds....
of a knot K in
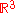 satisfies
satisfies
where
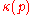 is the curvature at p, then K is an unknot. Therefore, for knotted curves,
is the curvature at p, then K is an unknot. Therefore, for knotted curves,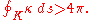
An example of a "physical" invariant is ropelength
Ropelength
In knot theory each realization of a link or knot has an associated ropelength. Intuitively this is the minimal length of an ideally flexible rope that is needed to tie a given link, or knot...
, which is the amount of 1-inch diameter rope needed to realize a particular knot type.
Other invariants
- Linking coefficient
- Finite type invariantFinite type invariantIn the mathematical theory of knots, a finite type invariant is a knot invariant that can be extended to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities...
(or Vassiliev or Vassiliev–Goussarov invariant) - Stick numberStick numberIn the mathematical theory of knots, the stick number is a knot invariant that intuitively gives the smallest number of straight "sticks" stuck end to end needed to form a knot...

