
Knot complement
Encyclopedia
In mathematics
, the knot complement of a tame knot K is the complement
of the interior of the embedding of a solid torus
into the 3-sphere
. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus. The knot complement is then
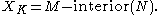
Note that the knot complement XK is a compact
3-manifold
; the boundary of XK and the boundary of the neighborhood N are homeomorphic to a two-torus
. Sometimes the ambient manifold M is understood to be 3-sphere
. Context is needed to determine the usage. There are analogous definitions of link
complement.
Many knot invariant
s, such as the knot group
, are really invariants of the complement of the knot. When the ambient space is the three-sphere no information is lost: the Gordon–Luecke theorem states that a knot is determined by its complement. That is, if K and K′ are two knots with homeomorphic complements then there is a homeomorphism of the three-sphere taking one knot to the other.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the knot complement of a tame knot K is the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the interior of the embedding of a solid torus
Solid torus
In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...
into the 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus. The knot complement is then
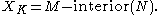
Note that the knot complement XK is a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
3-manifold
3-manifold
In mathematics, a 3-manifold is a 3-dimensional manifold. The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds.Phenomena in three dimensions...
; the boundary of XK and the boundary of the neighborhood N are homeomorphic to a two-torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. Sometimes the ambient manifold M is understood to be 3-sphere
3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It consists of the set of points equidistant from a fixed central point in 4-dimensional Euclidean space...
. Context is needed to determine the usage. There are analogous definitions of link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
complement.
Many knot invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
s, such as the knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
, are really invariants of the complement of the knot. When the ambient space is the three-sphere no information is lost: the Gordon–Luecke theorem states that a knot is determined by its complement. That is, if K and K′ are two knots with homeomorphic complements then there is a homeomorphism of the three-sphere taking one knot to the other.

