
Dowker notation
Encyclopedia
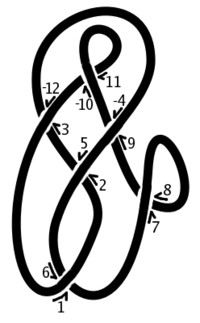
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of knot theory
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the Dowker notation, also called the Dowker–Thistlethwaite notation or code, for a knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
is a sequence of even integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. The notation is named after Clifford Hugh Dowker
Clifford Hugh Dowker
Clifford Hugh Dowker was a topologist known for his work in point-set topology and also for his contributions in category theory, sheaf theory and knot theory.-Biography:...
and Morwen Thistlethwaite
Morwen Thistlethwaite
Morwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
, who refined a notation originally due to Peter Guthrie Tait
Peter Guthrie Tait
Peter Guthrie Tait FRSE was a Scottish mathematical physicist, best known for the seminal energy physics textbook Treatise on Natural Philosophy, which he co-wrote with Kelvin, and his early investigations into knot theory, which contributed to the eventual formation of topology as a mathematical...
. To generate the Dowker notation, traverse the knot using an arbitrary starting point and direction. Label each of the n crossings with the numbers 1, ..., 2n in order of traversal (each crossing is visited and labelled twice), with the following modification: if the label is an even number and the strand followed crosses over at the crossing, then change the sign on the label to be a negative. When finished, each crossing will be labelled a pair of integers, one even and one odd. The Dowker notation is the sequence of even integer labels associated with the labels 1, 3, ..., 2n − 1 in turn.
For example, a knot diagram may have crossings labelled with the pairs (1, 6) (3, −12) (5, 2) (7, 8) (9, −4) and (11, −10). The Dowker notation for this labelling is the sequence: 6 −12 2 8 −4 −10.
A knot can be recovered from a Dowker sequence, but the recovered knot may differ from the original by being a reflection or (more generally) by having any connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
component reflected in the line between its entry/exit points – the Dowker notation is unchanged by these reflections. Knots tabulations typically consider only prime knot
Prime knot
In knot theory, a prime knot is a knot that is, in a certain sense, indecomposable. Specifically, it is a non-trivial knot which cannot be written as the knot sum of two non-trivial knots. Knots that are not prime are said to be composite. It can be a nontrivial problem to determine whether a...
s and disregard chirality
Chirality
Chirality is a property of asymmetry important in several branches of science. It may refer to:* Chirality , a property of molecules having a non-superimposable mirror image...
, so this ambiguity does not affect the tabulation.
The ménage problem
Ménage problem
In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of heterosexual couples at a dining table so that men and women alternate and nobody sits next to his or her partner...
, posed by Tait, concerns counting the number of different number sequences possible in this notation.
External links
- DT (Dowker-Thistlethwaite) Codes at the knot atlas

