Jones polynomial
Encyclopedia
In the mathematical field of knot theory
, the Jones polynomial is a knot polynomial
discovered by Vaughan Jones
in 1984. Specifically, it is an invariant
of an oriented knot
or link
which assigns to each oriented knot or link a Laurent polynomial in the variable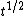
with integer coefficients.
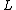, given as a knot diagram. We will define the Jones polynomial, 
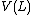, using Kauffman's bracket polynomial
, which we denote by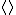
. Note that here the bracket polynomial is a Laurent polynomial in the variable 
with integer coefficients.
First, we define the auxiliary polynomial (also known as the normalized bracket polynomial)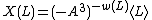
,
where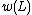
denotes the writhe
of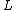
in its given diagram. The writhe of a diagram is the number of positive crossings (
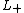in the figure below) minus the number of negative crossings (
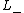). The writhe is not a knot invariant.
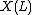is a knot invariant since it is invariant under changes of the diagram of 
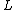by the three Reidemeister move
s. Invariance under type II and III Reidemeister moves follows from invariance of the bracket under those moves. The bracket polynomial is known to change by multiplication by
under a type I Reidemeister move. The definition of the 
polynomial given above is designed to nullify this change, since the writhe changes appropriately by +1 or -1 under type I moves.
Now make the substitutio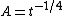n
in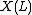 
to get the Jones polynomial 
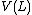. This results in a Laurent polynomial with integer coefficients in the variable 
.
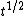, in statistical mechanics
.
Let a link L be given. A theorem of Alexander's states that it is the trace closure of a braid, say with n strands. Now define a representation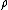
of the braid group on n strands, Bn, into the Temperley–Lieb algebra TLn with coefficients in 
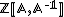and 
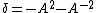. The standard braid generator 
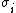is sent to 
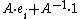, where 
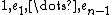are the standard generators of the Temperley–Lieb algebra. It can be checked easily that this defines a representation.
Take the braid word
obtained previously from L and compute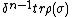 
where tr is the Markov trace. This gives 
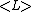, where < > is the bracket polynomial. This can be seen by considering, as Kauffman did, the Temperley–Lieb algebra as a particular diagram algebra.
An advantage of this approach is that one can pick similar representations into other algebras, such as the R-matrix representations, leading to "generalized Jones invariants".
:
where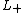
, 
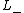, and 
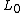are three oriented link diagrams that are identical except in one small region where they differ by the crossing changes or smoothing shown in the figure below:
.svg.png)
The definition of the Jones polynomial by the bracket makes it simple to show that for a knot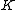 
, the Jones polynomial of its mirror image is given by substitution of 
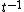for 
in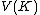 
. Thus, an amphichiral knot, a knot equivalent to its mirror image, has palindromic entries in its Jones polynomial. See the article on skein relation
for an example of a computation using these relations.
, the Jones polynomial of a given knot γ, can be obtained by considering Chern-Simons theory
on the three-sphere with gauge group SU(2), and computing the vacuum expectation value
of a Wilson loop
WF(γ), associated to γ, and the fundamental representation
F of SU(2).
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
, the Jones polynomial is a knot polynomial
Knot polynomial
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.-History:The first knot polynomial, the Alexander polynomial, was introduced by J. W...
discovered by Vaughan Jones
Vaughan Jones
Sir Vaughan Frederick Randal Jones, KNZM, FRS, FRSNZ is a New Zealand mathematician, known for his work on von Neumann algebras, knot polynomials and conformal field theory. He was awarded a Fields Medal in 1990, and famously wore a New Zealand rugby jersey when he accepted the prize...
in 1984. Specifically, it is an invariant
Knot invariant
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...
of an oriented knot
Knot (mathematics)
In mathematics, a knot is an embedding of a circle in 3-dimensional Euclidean space, R3, considered up to continuous deformations . A crucial difference between the standard mathematical and conventional notions of a knot is that mathematical knots are closed—there are no ends to tie or untie on a...
or link
Link (knot theory)
In mathematics, a link is a collection of knots which do not intersect, but which may be linked together. A knot can be described as a link with one component. Links and knots are studied in a branch of mathematics called knot theory...
which assigns to each oriented knot or link a Laurent polynomial in the variable
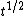with integer coefficients.Definition by the bracket
Suppose we have an oriented link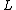, given as a knot diagram. We will define the Jones polynomial, 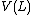, using Kauffman's bracket polynomialBracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
, which we denote by
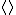. Note that here the bracket polynomial is a Laurent polynomial in the variable with integer coefficients.First, we define the auxiliary polynomial (also known as the normalized bracket polynomial)
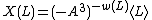,where
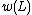denotes the writheWrithe
In knot theory, the writhe is a property of an oriented link diagram. The writhe is the total number of positive crossings minus the total number of negative crossings....
of
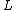in its given diagram. The writhe of a diagram is the number of positive crossings ( 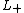in the figure below) minus the number of negative crossings (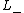). The writhe is not a knot invariant. 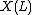is a knot invariant since it is invariant under changes of the diagram of 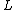by the three Reidemeister moveReidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s. Invariance under type II and III Reidemeister moves follows from invariance of the bracket under those moves. The bracket polynomial is known to change by multiplication by
under a type I Reidemeister move. The definition of the polynomial given above is designed to nullify this change, since the writhe changes appropriately by +1 or -1 under type I moves.Now make the substitution
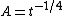in 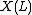to get the Jones polynomial 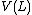. This results in a Laurent polynomial with integer coefficients in the variable 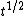.Definition by braid representation
Jones' original formulation of his polynomial came from his study of operator algebras. In Jones' approach, it resulted from a kind of "trace" of a particular braid representation into an algebra which originally arose while studying certain models, e.g. the Potts modelPotts model
In statistical mechanics, the Potts model, a generalization of the Ising model, is a model of interacting spins on a crystalline lattice. By studying the Potts model, one may gain insight into the behaviour of ferromagnets and certain other phenomena of solid state physics...
, in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
.
Let a link L be given. A theorem of Alexander's states that it is the trace closure of a braid, say with n strands. Now define a representation
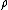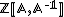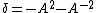of the braid group on n strands, Bn, into the Temperley–Lieb algebra TLn with coefficients in and . The standard braid generator 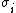is sent to 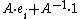, where 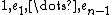are the standard generators of the Temperley–Lieb algebra. It can be checked easily that this defines a representation.Take the braid word
obtained previously from L and compute 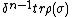where tr is the Markov trace. This gives 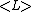, where < > is the bracket polynomial. This can be seen by considering, as Kauffman did, the Temperley–Lieb algebra as a particular diagram algebra.An advantage of this approach is that one can pick similar representations into other algebras, such as the R-matrix representations, leading to "generalized Jones invariants".
Properties
The Jones polynomial is characterized by the fact that it takes the value 1 on any diagram of the unknot and satisfies the following skein relationSkein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
:
where
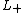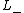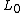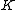, , and are three oriented link diagrams that are identical except in one small region where they differ by the crossing changes or smoothing shown in the figure below:, the Jones polynomial of its mirror image is given by substitution of 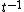for in 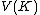. Thus, an amphichiral knot, a knot equivalent to its mirror image, has palindromic entries in its Jones polynomial. See the article on skein relationSkein relation
A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One tool used to answer such questions is a knot polynomial which is an invariant of the knot. If two diagrams have different polynomials, they represent different knots. The reverse may not...
for an example of a computation using these relations.
Link with Chern-Simons theory
As first shown by Edward WittenEdward Witten
Edward Witten is an American theoretical physicist with a focus on mathematical physics who is currently a professor of Mathematical Physics at the Institute for Advanced Study....
, the Jones polynomial of a given knot γ, can be obtained by considering Chern-Simons theory
Chern-Simons theory
The Chern–Simons theory is a 3-dimensional topological quantum field theory of Schwarz type, introduced by Edward Witten. It is so named because its action is proportional to the integral of the Chern–Simons 3-form....
on the three-sphere with gauge group SU(2), and computing the vacuum expectation value
Vacuum expectation value
In quantum field theory the vacuum expectation value of an operator is its average, expected value in the vacuum. The vacuum expectation value of an operator O is usually denoted by \langle O\rangle...
of a Wilson loop
Wilson loop
In gauge theory, a Wilson loop is a gauge-invariant observable obtained from the holonomy of the gauge connection around a given loop...
WF(γ), associated to γ, and the fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
F of SU(2).
Open problems
- Is there a nontrivial knot with Jones polynomial equal to that of the unknotUnknotThe unknot arises in the mathematical theory of knots. Intuitively, the unknot is a closed loop of rope without a knot in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped, to the standard unknot, i.e. the embedding of the...
? It is known that there are nontrivial links with Jones polynomial equal to that of the corresponding unlinkUnlinkIn the mathematical field of knot theory, the unlink is a link that is equivalent to finitely many disjoint circles in the plane.- Properties :...
s by the work of Morwen ThistlethwaiteMorwen ThistlethwaiteMorwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...
.
External links
- Links with trivial Jones polynomial by Morwen ThistlethwaiteMorwen ThistlethwaiteMorwen B. Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory, and Rubik's cube group theory.-Biography:...