The unknot arises in the mathematical theory of knots

Knot theory

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...

. Intuitively, the unknot is a closed loop of rope without a knot

Knot

A knot is a method of fastening or securing linear material such as rope by tying or interweaving. It may consist of a length of one or several segments of rope, string, webbing, twine, strap, or even chain interwoven such that the line can bind to itself or to some other object—the "load"...

 in it. A knot theorist would describe the unknot as an image of any embedding that can be deformed, i.e. ambient-isotoped

Ambient isotopy

In the mathematical subject of topology, an ambient isotopy, also called an h-isotopy, is a kind of continuous distortion of an "ambient space", a manifold, taking a submanifold to another submanifold. For example in knot theory, one considers two knots the same if one can distort one knot into the...

, to the standard unknot, i.e. the embedding of the circle as a geometrically round circle. The unknot is also called the trivial knot. An unknot is the identity element

Identity element

In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...

 with respect to the knot sum operation.

Unknotting problem

Deciding if a particular knot is the unknot was a major driving force behind knot invariant

Knot invariant

In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the...

s, since it was thought this approach would possibly give an efficient algorithm to recognize the unknot

Unknotting problem

In mathematics, the unknotting problem is the problem of algorithmically recognizing the unknot, given some representation of a knot, e.g., a knot diagram. There are several types of unknotting algorithms...

 from some presentation such as a knot diagram. Currently there are several well-known unknot recognition algorithms (not using invariants), but they are either known to be inefficient or have no efficient implementation. It is not known whether many of the current invariants, such as finite type invariant

Finite type invariant

In the mathematical theory of knots, a finite type invariant is a knot invariant that can be extended to an invariant of certain singular knots that vanishes on singular knots with m + 1 singularities and does not vanish on some singular knot with 'm' singularities...

s, are a complete invariant of the unknot, but knot Floer homology is known to detect the unknot. Even if they were, the problem of computing them efficiently remains.

Examples

Many useful practical knots are actually the unknot, including all knots which can be tied in the bight

Bight (knot)

In knot tying, a bight is a curved section, slack part, or loop between the two ends of a rope, string, or yarn. The term is also used in a more specific way when describing Turk's head knots, indicating how many repetitions of braiding are made in the circuit of a given knot.-Slipped knot:In order...

. Other noteworthy unknots are those that consist of rigid line segments connected by universal joints at their endpoints (linkages), that yet cannot be reconfigured into a convex polygon, thus acquiring the name stuck unknots.

Invariants

The Alexander polynomial

Alexander polynomial

In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...

, Conway polynomial

Conway polynomial

In mathematics, Conway polynomial can refer to:* the Alexander–Conway polynomial in knot theory* the Conway polynomial...

 and Jones polynomial of the unknot are trivial:


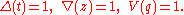
No other knot with 10 or fewer crossings

Crossing number (knot theory)

In the mathematical area of knot theory, the crossing number of a knot is the minimal number of crossings of any diagram of the knot. It is a knot invariant....

 has trivial Alexander polynomial, but the Kinoshita-Terasaka knot and Conway knot (both of which have 11 crossings) have the same Alexander and Conway polynomials as the unknot. It is an open problem whether any non-trivial knot has the same Jones polynomial as the unknot.

The knot group

Knot group

In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....

 of the unknot is an infinite cyclic group

Cyclic group

In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...

, and the knot complement

Knot complement

In mathematics, the knot complement of a tame knot K is the complement of the interior of the embedding of a solid torus into the 3-sphere. To make this precise, suppose that K is a knot in a three-manifold M. Let N be a thickened neighborhood of K; so N is a solid torus...

 is homeomorphic

Homeomorphism

In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...

 to a solid torus

Solid torus

In mathematics, a solid torus is a topological space homeomorphic to S^1 \times D^2, i.e. the cartesian product of the circle with a two dimensional disc endowed with the product topology. The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary...

.