Bose gas
Encyclopedia
An ideal Bose gas is a quantum-mechanical version of a classical ideal gas
. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics
. The statistical mechanics of bosons were developed by Satyendra Nath Bose
for photons
, and extended to massive particles by Albert Einstein
who realized that an ideal gas of bosons would form a condensate at a low enough temperature, unlike a classical ideal gas. This condensate is known as a Bose–Einstein condensate
.
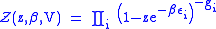
where each term in the product corresponds to a particular energy εi , gi is the number of states with energy εi , z is the absolute activity (or "fugacity"), which may also be expressed in terms of the chemical potential
μ by defining:
and β defined as:
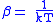
where k is Boltzmann's constant and T is the temperature
. All thermodynamic quantities may be derived from the grand partition function and we will consider all thermodynamic quantities to be functions of only the three variables z , β (or T ), and V . All partial derivatives are taken with respect to one of these three variables while the other two are held constant. It is more convenient to deal with the dimensionless grand potential defined as:
Following the procedure described in the gas in a box
article, we can apply the Thomas-Fermi approximation
which assumes that the average energy is large compared to the energy difference between levels so that the above sum may be replaced by an integral:
The degeneracy dg may be expressed for many different situations by the general formula:
where α is a constant,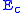
is a "critical energy", and Γ is the Gamma function
. For example, for a massive Bose gas in a box
, α=3/2 and the critical energy is given by:
where Λ is the thermal wavelength. For a massive Bose gas in a harmonic trap
we will have α=3 and the critical energy is given by:
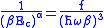
where V(r)=mω2r2/2 is the harmonic potential. It is seen that Ec is a function of volume only.
We can solve the equation for the grand potential by integrating the Taylor series of the integrand term by term, or by realizing that it is proportional to the Mellin transform
of the Li1(z exp(-β E)) where Lis(x) is the polylogarithm function. The solution is:
The problem with this continuum approximation for a Bose gas is that the ground state has been effectively ignored, giving a degeneracy of zero for zero energy. This inaccuracy becomes serious when dealing with the Bose–Einstein condensate
and will be dealt with in the next section.
is found from the grand potential by
The polylogarithm term must remain real and positive, and the maximum value it can possibly have is at z=1 where it is equal to ζ(α) where ζ is the Riemann zeta function. For a fixed N , the largest possible value that β can have is a critical value βc where
This corresponds to a critical temperature Tc=1/kβc below which the Thomas-Fermi approximation breaks down. The above equation can be solved for the critical temperature:
For example, for
and using the above noted value of 
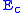yields
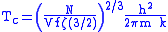
Again, we are presently unable to calculate results below the critical temperature, because the particle numbers using the above equation become negative. The problem here is that the Thomas-Fermi approximation has set the degeneracy of the ground state to zero, which is wrong. There is no ground state to accept the condensate and so the equation breaks down. It turns out, however, that the above equation gives a rather accurate estimate of the number of particles in the excited states, and it is not a bad approximation to simply "tack on" a ground state term:
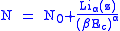
where N0 is the number of particles in the ground state condensate:
This equation can now be solved down to absolute zero in temperature. Figure 1 shows the results of the solution to this equation for α=3/2, with k=εc=1 which corresponds to a gas of bosons in a box
. The solid black line is the fraction of excited states 1-N0/N for N =10,000 and the dotted black line is the solution for N =1000. The blue lines are the fraction of condensed particles N0/N The red lines plot values of the
negative of the chemical potential μ and the green lines plot the corresponding values of z . The horizontal axis is the normalized temperature τ defined by
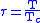
It can be seen that each of these parameters become linear in τα in the limit of low temperature and, except for the chemical potential, linear in 1/τα in the limit of high temperature. As the number of particles increases, the condensed and excited fractions tend towards a discontinuity at the critical temperature.
The equation for the number of particles can be written in terms of the normalized temperature as:
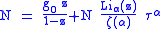
For a given N and τ, this equation can be solved for τα and then a series solution for z can be found by the method of inversion of series, either in powers of τα or as an asymptotic expansion in inverse powers of τα. From these expansions, we can find the behavior of the gas near T =0 and in the Maxwell-Boltzmann as T approaches infinity. In particular, we are interested in the limit as N approaches infinity, which can be easily determined from these expansions.
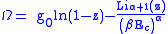
All thermodynamic properties may now be computed from the grand potential. The following table lists various thermodynamic quantities calculated in the limit of low temperature and high temperature, and in the limit of infinite particle number. An equal sign (=) indicates an exact result, while an approximation symbol indicates that only the first few terms of a series in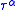
is shown.
It is seen that all quantities approach the values for a classical ideal gas
in
the limit of large temperature. The above values can be used to calculate other
thermodynamic quantities. For example, the relationship between internal energy and
the product of pressure and volume is the same as that for a classical ideal gas over
all temperatures:
A similar situation holds for the specific heat at constant volume
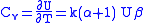
The entropy is given by:
Note that in the limit of high temperature, we have
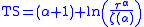
which, for α=3/2 is simply a restatement of the Sackur-Tetrode equation
. In one dimension bosons with delta interaction behave as fermions, they obey Pauli exclusion principle
. In one dimension Bose gas with delta interaction can be solved exactly by Bethe ansatz
. The bulk free energy and thermodynamic potentials were calculated by Chen Nin Yang. In one dimensional case correlation functions also were evaluated. The In one dimension Bose gas is equivalent to quantum non-linear Schroedinger equation.
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
. It is composed of bosons, which have an integer value of spin, and obey Bose–Einstein statistics
Bose–Einstein statistics
In statistical mechanics, Bose–Einstein statistics determines the statistical distribution of identical indistinguishable bosons over the energy states in thermal equilibrium.-Concept:...
. The statistical mechanics of bosons were developed by Satyendra Nath Bose
Satyendra Nath Bose
Satyendra Nath Bose FRS was an Indian mathematician and physicist noted for his collaboration with Albert Einstein in developing a theory regarding the gaslike qualities of electromagnetic radiation. He is best known for his work on quantum mechanics in the early 1920s, providing the foundation...
for photons
Photon gas
In physics, a photon gas is a gas-like collection of photons, which has many of the same properties of a conventional gas like hydrogen or neon - including pressure, temperature, and entropy...
, and extended to massive particles by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
who realized that an ideal gas of bosons would form a condensate at a low enough temperature, unlike a classical ideal gas. This condensate is known as a Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
.
Thomas–Fermi approximation
The thermodynamics of an ideal Bose gas is best calculated using the grand partition function. The grand partition function for a Bose gas is given by: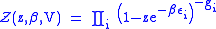where each term in the product corresponds to a particular energy εi , gi is the number of states with energy εi , z is the absolute activity (or "fugacity"), which may also be expressed in terms of the chemical potential
Chemical potential
Chemical potential, symbolized by μ, is a measure first described by the American engineer, chemist and mathematical physicist Josiah Willard Gibbs. It is the potential that a substance has to produce in order to alter a system...
μ by defining:
and β defined as:
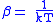
where k is Boltzmann's constant and T is the temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
. All thermodynamic quantities may be derived from the grand partition function and we will consider all thermodynamic quantities to be functions of only the three variables z , β (or T ), and V . All partial derivatives are taken with respect to one of these three variables while the other two are held constant. It is more convenient to deal with the dimensionless grand potential defined as:
Following the procedure described in the gas in a box
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
article, we can apply the Thomas-Fermi approximation
Thomas-Fermi model
The Thomas–Fermi model, named after Llewellyn Thomas and Enrico Fermi, is a quantum mechanical theory for the electronic structure of many-body systems developed semiclassically shortly after the introduction of the Schrödinger equation...
which assumes that the average energy is large compared to the energy difference between levels so that the above sum may be replaced by an integral:
The degeneracy dg may be expressed for many different situations by the general formula:
where α is a constant,
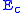is a "critical energy", and Γ is the Gamma functionGamma function
In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. For example, for a massive Bose gas in a box
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
, α=3/2 and the critical energy is given by:
where Λ is the thermal wavelength. For a massive Bose gas in a harmonic trap
Gas in a harmonic trap
The results of the quantum harmonic oscillator can be used to look at the equilibrium situation for a quantum ideal gas in a harmonic trap, which is a harmonic potential containing a large number of particles that do not interact with each other except for instantaneous thermalizing collisions...
we will have α=3 and the critical energy is given by:
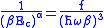
where V(r)=mω2r2/2 is the harmonic potential. It is seen that Ec is a function of volume only.
We can solve the equation for the grand potential by integrating the Taylor series of the integrand term by term, or by realizing that it is proportional to the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
of the Li1(z exp(-β E)) where Lis(x) is the polylogarithm function. The solution is:
The problem with this continuum approximation for a Bose gas is that the ground state has been effectively ignored, giving a degeneracy of zero for zero energy. This inaccuracy becomes serious when dealing with the Bose–Einstein condensate
Bose–Einstein condensate
A Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
and will be dealt with in the next section.
Inclusion of the ground state
The total number of particlesParticle number
The particle number of a thermodynamic system, conventionally indicated with the letter N, is the number of constituent particles in that system. The particle number is a fundamental parameter in thermodynamics which is conjugate to the chemical potential. Unlike most physical quantities, particle...
is found from the grand potential by
The polylogarithm term must remain real and positive, and the maximum value it can possibly have is at z=1 where it is equal to ζ(α) where ζ is the Riemann zeta function. For a fixed N , the largest possible value that β can have is a critical value βc where
This corresponds to a critical temperature Tc=1/kβc below which the Thomas-Fermi approximation breaks down. The above equation can be solved for the critical temperature:
For example, for
and using the above noted value of 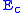yields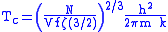Again, we are presently unable to calculate results below the critical temperature, because the particle numbers using the above equation become negative. The problem here is that the Thomas-Fermi approximation has set the degeneracy of the ground state to zero, which is wrong. There is no ground state to accept the condensate and so the equation breaks down. It turns out, however, that the above equation gives a rather accurate estimate of the number of particles in the excited states, and it is not a bad approximation to simply "tack on" a ground state term:
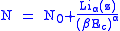
where N0 is the number of particles in the ground state condensate:
Gas in a box
In quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
. The solid black line is the fraction of excited states 1-N0/N for N =10,000 and the dotted black line is the solution for N =1000. The blue lines are the fraction of condensed particles N0/N The red lines plot values of the
negative of the chemical potential μ and the green lines plot the corresponding values of z . The horizontal axis is the normalized temperature τ defined by
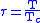
It can be seen that each of these parameters become linear in τα in the limit of low temperature and, except for the chemical potential, linear in 1/τα in the limit of high temperature. As the number of particles increases, the condensed and excited fractions tend towards a discontinuity at the critical temperature.
The equation for the number of particles can be written in terms of the normalized temperature as:
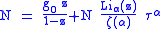
For a given N and τ, this equation can be solved for τα and then a series solution for z can be found by the method of inversion of series, either in powers of τα or as an asymptotic expansion in inverse powers of τα. From these expansions, we can find the behavior of the gas near T =0 and in the Maxwell-Boltzmann as T approaches infinity. In particular, we are interested in the limit as N approaches infinity, which can be easily determined from these expansions.
Thermodynamics
Adding the ground state to the equation for the particle number corresponds to adding the equivalent ground state term to the grand potential: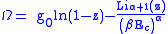All thermodynamic properties may now be computed from the grand potential. The following table lists various thermodynamic quantities calculated in the limit of low temperature and high temperature, and in the limit of infinite particle number. An equal sign (=) indicates an exact result, while an approximation symbol indicates that only the first few terms of a series in
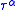is shown.| Quantity | General |  |
 |
|---|---|---|---|
| z |  |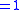
 |
|
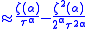Vapor fraction |
 |
 |
 |
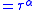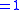Equation of state |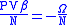
 |
 |
 |
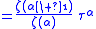Gibbs Free Energy |
 |
 |
 |
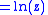It is seen that all quantities approach the values for a classical ideal gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
in
the limit of large temperature. The above values can be used to calculate other
thermodynamic quantities. For example, the relationship between internal energy and
the product of pressure and volume is the same as that for a classical ideal gas over
all temperatures:
A similar situation holds for the specific heat at constant volume
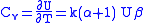
The entropy is given by:
Note that in the limit of high temperature, we have
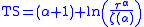
which, for α=3/2 is simply a restatement of the Sackur-Tetrode equation
Sackur-Tetrode equation
The Sackur–Tetrode equation is an expression for the entropy of a monatomic classical ideal gas which incorporates quantum considerations which give a more detailed description of its regime of validity....
. In one dimension bosons with delta interaction behave as fermions, they obey Pauli exclusion principle
Pauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
. In one dimension Bose gas with delta interaction can be solved exactly by Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
. The bulk free energy and thermodynamic potentials were calculated by Chen Nin Yang. In one dimensional case correlation functions also were evaluated. The In one dimension Bose gas is equivalent to quantum non-linear Schroedinger equation.
See also
- Gas in a boxGas in a boxIn quantum mechanics, the results of the quantum particle in a box can be used to look at the equilibrium situation for a quantum ideal gas in a box which is a box containing a large number of molecules which do not interact with each other except for instantaneous thermalizing collisions...
- Debye modelDebye modelIn thermodynamics and solid state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice as phonons in a box, in contrast to the Einstein model, which treats the...
- Bose–Einstein condensateBose–Einstein condensateA Bose–Einstein condensate is a state of matter of a dilute gas of weakly interacting bosons confined in an external potential and cooled to temperatures very near absolute zero . Under such conditions, a large fraction of the bosons occupy the lowest quantum state of the external potential, at...
- Bose–Einstein condensation: a network theory approach