
Fluid statics
Encyclopedia

Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
of fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s at rest, and is a sub-field within fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable
Mechanical equilibrium
A standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
equilibrium
Hydrostatic equilibrium
Hydrostatic equilibrium or hydrostatic balance is the condition in fluid mechanics where a volume of a fluid is at rest or at constant velocity. This occurs when compression due to gravity is balanced by a pressure gradient force...
. The use of fluid to do work is called hydraulics
Hydraulics
Hydraulics is a topic in applied science and engineering dealing with the mechanical properties of liquids. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on the engineering uses of fluid properties. In fluid power, hydraulics is used for the generation, control,...
, and the science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
of fluids in motion is fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
.
Pressure in fluids at rest
Due to the fundamental nature of fluids, a fluid cannot remain at rest under the presence of a shear stressShear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
. However, fluids can exert pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
normal
Surface normal
A surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
to any contacting surface. If a point in the fluid is thought of as an infinitesimally small cube, then it follows from the principles of equilibrium that the pressure on every side of this unit of fluid must be equal. If this were not the case, the fluid would move in the direction of the resulting force. Thus, the pressure on a fluid at rest is isotropic; i.e., it acts with equal magnitude in all directions. This characteristic allows fluids to transmit force through the length of pipes or tubes; i.e., a force applied to a fluid in a pipe is transmitted, via the fluid, to the other end of the pipe.
This concept was first formulated, in a slightly extended form, by the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
and philosopher Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
in 1647 and would later be known as Pascal's law
Pascal's law
In the physical sciences, Pascal's law or the Principle of transmission of fluid-pressure states that "pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions throughout the fluid such that the pressure ratio remains the same." The law was established...
. This law has many important applications in hydraulics
Hydraulics
Hydraulics is a topic in applied science and engineering dealing with the mechanical properties of liquids. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on the engineering uses of fluid properties. In fluid power, hydraulics is used for the generation, control,...
.
Hydrostatic pressure
See also vertical pressure variationVertical pressure variation
Vertical pressure variation is the variation in pressure as a function of elevation. Depending on the fluid in question and the context being referred to, it may also vary significantly in dimensions perpendicular to elevation as well, and these variations have relevance in the context of pressure...
.
Hydrostatic pressure is the pressure exerted by a fluid at equilibrium due to the force of gravity. A fluid in this condition is known as a hydrostatic fluid
Hydrostatic fluid
In atmospheric dynamics and fluid dynamics, a hydrostatic fluid is a fluid in which fluid stresses act isotropically and fluid elements are in local equilibrium with one another...
. The hydrostatic pressure can be determined from a control volume analysis of an infinitesimally small cube of fluid. Since pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
is defined as the force exerted on a test area (p = F/A, with p: pressure, F: force normal to area A, A: area), and the only force acting on any such small cube of fluid is the weight of the fluid column above it, hydrostatic pressure can be calculated according to the following formula:
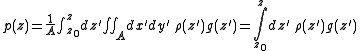 ,
,where:
- p is the hydrostatic pressure (Pa),
- ρ is the fluid densityDensityThe mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
(kg/m3), - g is gravitational acceleration (m/s2),
- A is the test area (m2),
- z is the height (parallel to the direction of gravity) of the test area (m),
- z0 is the height of the zero reference point of the pressure (m).
For water and other liquids, this integral can be simplified significantly for many practical applications, based on the following two assumptions: Since many liquids can be considered incompressible, a reasonably good estimation can be made from assuming a constant density throughout the liquid. (The same assumption cannot be made within a gaseous environment.) Also, since the height h of the fluid column between z and z0 is often reasonably small compared to the radius of the Earth, one can neglect the variation of g. Under these circumstances, the integral boils down to the simple formula:
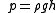 ,
,where h is the height z-z0 of the liquid column between the test volume and the zero reference point of the pressure. Note that this reference point should lie at or below the surface of the liquid. Otherwise, one has to split the integral into two (or more) terms with the constant ρliquid and ρ(z')above. For example, the absolute pressure compared to vacuum is :
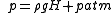 ,
,where H is the total height of the liquid column above the test area the surface, and patm is the atmospheric pressure
Atmospheric pressure
Atmospheric pressure is the force per unit area exerted into a surface by the weight of air above that surface in the atmosphere of Earth . In most circumstances atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point...
, i.e., the pressure calculated from the remaining integral over the air column from the liquid surface to infinity.
Hydrostatic pressure has been used in the preservation of foods in a process called pascalization
Pascalization
Pascalization, bridgmanization, or high pressure processing , is a method of preserving and sterilizing food, in which a product is processed under very high pressure, leading to the inactivation of certain microorganisms and enzymes in the food...
.
Atmospheric pressure
Statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
shows that, for a gas of constant temperature, T, its pressure, p will vary with height, h, as:
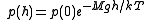
where:
- g = the acceleration due to gravityStandard gravityStandard gravity, or standard acceleration due to free fall, usually denoted by g0 or gn, is the nominal acceleration of an object in a vacuum near the surface of the Earth. It is defined as precisely , or about...
- T = Absolute temperature
- k = Boltzmann constant
- M = mass of a single moleculeMoleculeA molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
of gas - p = pressure
- h = height
This is known as the barometric formula
Barometric formula
The barometric formula, sometimes called the exponential atmosphere or isothermal atmosphere, is a formula used to model how the pressure of the air changes with altitude.-Pressure equations:...
, and may be derived from assuming the pressure is hydrostatic.
If there are multiple types of molecules in the gas, the partial pressure
Partial pressure
In a mixture of ideal gases, each gas has a partial pressure which is the pressure which the gas would have if it alone occupied the volume. The total pressure of a gas mixture is the sum of the partial pressures of each individual gas in the mixture....
of each type will be given by this equation. Under most conditions, the distribution of each species of gas is independent of the other species.
Buoyancy
Any body of arbitrary shape which is immersed, partly or fully, in a fluid will experience the action of a net force in the opposite direction of the local pressure gradient. If this pressure gradient arises from gravity, the net force is in the vertical direction opposite that of the gravitational force. This vertical force is termed buoyancy or buoyant force and is equal in magnitude, but opposite in direction, to the weight of the displaced fluid.In the case of a ship
Ship
Since the end of the age of sail a ship has been any large buoyant marine vessel. Ships are generally distinguished from boats based on size and cargo or passenger capacity. Ships are used on lakes, seas, and rivers for a variety of activities, such as the transport of people or goods, fishing,...
, for instance, its weight is balanced by shear force from the displaced water, allowing it to float. If more cargo is loaded onto the ship, it would sink more into the water - displacing more water and thus receive a higher buoyant force to balance the increased weight.
Discovery of the principle of buoyancy is attributed to Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
.
Liquids-fluids with free surfaces
Liquids can have free surfaces at which they interface with gases, or with a vacuumVacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
. In general, the lack of the ability to sustain a shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
entails that free surfaces rapidly adjust towards an equilibrium. However, on small length scales, there is an important balancing force from surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
.
Capillary action
When liquids are constrained in vessels whose dimensions are small, compared to the relevant length scales, surface tensionSurface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
effects become important leading to the formation of a meniscus
Meniscus
The meniscus is the curve in the upper surface of a liquid close to the surface of the container or another object, caused by surface tension. It can be either convex or concave. A convex meniscus occurs when the molecules have a stronger attraction to each other than to the material of the...
through capillary action
Capillary action
Capillary action, or capilarity, is the ability of a liquid to flow against gravity where liquid spontanously rise in a narrow space such as between the hair of a paint-brush, in a thin tube, or in porous material such as paper or in some non-porous material such as liquified carbon fiber, or in a...
. This capillary action has profound consequences for biological systems as it is part of one of the two driving mechanisms of the flow of water in plant
Plant
Plants are living organisms belonging to the kingdom Plantae. Precise definitions of the kingdom vary, but as the term is used here, plants include familiar organisms such as trees, flowers, herbs, bushes, grasses, vines, ferns, mosses, and green algae. The group is also called green plants or...
xylem
Xylem
Xylem is one of the two types of transport tissue in vascular plants. . The word xylem is derived from the Classical Greek word ξυλον , meaning "wood"; the best-known xylem tissue is wood, though it is found throughout the plant...
, the transpirational pull.
Drops
Without surface tension, dropDrop (liquid)
A drop or droplet is a small column of liquid, bounded completely or almost completely by free surfaces. A drop may form when liquid accumulates at the lower end of a tube or other surface boundary, producing a hanging drop called a pendant drop...
s would not be able to form. The dimensions and stability of drops are determined by surface tension.The drop's surface tension is directly proportional to the cohesion property of the fluid.

