Cholesky decomposition
Encyclopedia
In linear algebra
, the Cholesky decomposition or Cholesky triangle is a decomposition
of a Hermitian, positive-definite
matrix
into the product of a lower triangular matrix and its conjugate transpose
. It was discovered by André-Louis Cholesky
for real matrices. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition
for solving systems of linear equations. In a loose, metaphorical sense, this can be thought of as the matrix analogue of taking the square root of a number.
where L is a lower triangular matrix with strictly positive diagonal entries, and L* denotes the conjugate transpose
of L. This is the Cholesky decomposition.
The Cholesky decomposition is unique: given a Hermitian, positive-definite matrix A, there is only one lower triangular matrix L with strictly positive diagonal entries such that A = LL*. The converse holds trivially: if A can be written as LL* for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite.
The requirement that L have strictly positive diagonal entries can be dropped to extend the factorization to the positive-semidefinite case. The statement then reads: a square matrix A has a Cholesky decomposition if and only if A is Hermitian and positive semi-definite. Cholesky factorizations for positive-semidefinite matrices are not unique in general.
In the special case that A is a symmetric positive-definite matrix with real entries, L has real entries as well.
problems are of this form. It may also happen that matrix A comes from an energy functional which must be positive from physical considerations; this happens frequently in the numerical solution of partial differential equation
s.
of partial second derivatives formed by repeated rank 1 updates at each iteration. Two well-known update formulae are called Davidon-Fletcher-Powell (DFP) and Broydon-Fletcher-Goldfarb-Shanno (BFGS). Loss of the positive-definite condition through round-off error is avoided if rather than updating an approximation to the inverse of the Hessian, one updates the Cholesky decomposition of an approximation of the Hessian matrix itself.
for simulating systems with multiple correlated variables: The covariance matrix
is decomposed, to give the lower-triangular L. Applying this to a vector of uncorrelated samples, u, produces a sample vector Lu with the covariance properties of the system being modeled.
s commonly use the Cholesky decomposition to choose a set of so-called sigma points. The Kalman filter tracks the average state of a system as a vector x of length N and covariance as an N-by-N matrix P. The matrix P is always positive semi-definite, and can be decomposed into LLT. The columns of L can be added and subtracted from the mean x to form a set of 2N vectors called sigma points. These sigma points completely capture the mean and covariance of the system state.
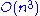in general. The algorithms described below all involve about n3/3 FLOP
s, where n is the size of the matrix A. Hence, they are half the cost of the LU decomposition
, which uses 2n3/3 FLOPs (see Trefethen and Bau 1997).
Which of the algorithms below is faster depends on the details of the implementation. Generally, the first algorithm will be slightly slower because it accesses the data in a more irregular manner.
.
The recursive algorithm starts with i := 1 and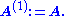
At step i, the matrix A(i) has the following form: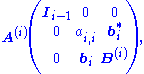
where Ii−1 denotes the identity matrix
of dimension i − 1.
If we now define the matrix Li by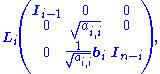
then we can write A(i) as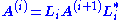
where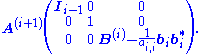
Note that bi bi* is an outer product
, therefore this algorithm is called the outer product version in (Golub & Van Loan).
We repeat this for i from 1 to n. After n steps, we get A(n+1) = I. Hence, the lower triangular matrix L we are looking for is calculated as
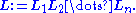
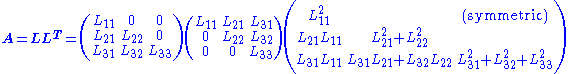
we obtain the following formula for the entries of L:
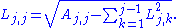
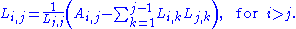
The expression under the square root
is always positive if A is real and positive-definite.
For complex Hermitian matrix, the following formula applies:
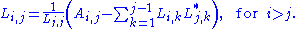
So we can compute the (i, j) entry if we know the entries to the left and above. The computation is usually arranged in either of the following orders.
system of linear equations. If the LU decomposition is used, then the algorithm is unstable unless we use some sort of pivoting strategy. In the latter case, the error depends on the so-called growth factor of the matrix, which is usually (but not always) small.
Now, suppose that the Cholesky decomposition is applicable. As mentioned above, the algorithm will be twice as fast. Furthermore, no pivoting is necessary and the error will always be small. Specifically, if we want to solve Ax = b, and y denotes the computed solution, then y solves the disturbed system (A + E)y = b where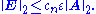
Here, || ||2 is the matrix 2-norm, cn is a small constant depending on n, and ε denotes the unit round-off.
There is one small problem with the Cholesky decomposition. Note that we must compute square roots in order to find the Cholesky decomposition. If the matrix is real symmetric and positive definite, then the numbers under the square roots are always positive in exact arithmetic. Unfortunately, the numbers can become negative because of round-off error
s, in which case the algorithm cannot continue. However, this can only happen if the matrix is very ill-conditioned.
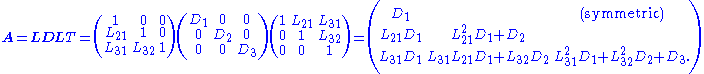
This form eliminates the need to take square roots. When A is positive definite the elements of the diagonal matrix D are all positive. However this factorization may be used for most invertible symmetric matrices; an example of an invertible matrix whose decomposition is undefined is one where the first entry is zero.
If A is real, the following recursive relations apply for the entries of D and L: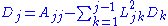
For complex Hermitian matrix A, the following formula applies: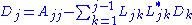
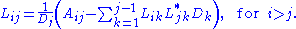
The LDLT and LLT factorizations (note that L is different between the two) may be easily related:
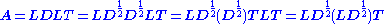
The last expression is the product of a lower triangular matrix and its transpose, as is the LLT factorization.
If A is an n-by-n positive semi-definite matrix, then the sequence {Ak} = {A + (1/k)In} consists of positive definite matrices. (This is an immediate consequence of, for example, the spectral mapping theorem for the polynomial functional calculus.) Also,
in operator norm
. From the positive definite case, each Ak has Cholesky decomposition Ak = LkLk*. By property of the operator norm,
So {Lk} is a bounded set in the Banach space
of operators, therefore relatively compact (because the underlying vector space is finite dimensional). Consequently it has a convergent subsequence, also denoted by {Lk}, with limit L. It can be easily checked that this L has the desired properties, i.e. A = LL* and L is lower triangular with non-negative diagonal entries: for all x and y,
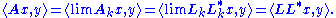
Therefore A = LL*. Because the underlying vector space is finite dimensional, all topologies on the space of operators are equivalent. So Lk tends to L in norm means Lk tends to L entrywise. This in turn implies that, since each Lk is lower triangular with non-negative diagonal entries, L is also.
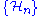be a sequence of Hilbert spaces. Consider the operator matrix
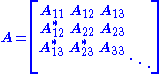
acting on the direct sum
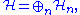
where each
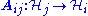
is a bounded operator
. If A is positive (semidefinite) in the sense that for all finite k and for any
we have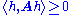
, then there exists a lower triangular operator matrix L such that A = LL*. One can also take the diagonal entries of L to be positive.
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, the Cholesky decomposition or Cholesky triangle is a decomposition
Matrix decomposition
In the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
of a Hermitian, positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
into the product of a lower triangular matrix and its conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
. It was discovered by André-Louis Cholesky
André-Louis Cholesky
André-Louis Cholesky was a French military officer and mathematician, born in Montguyon, France....
for real matrices. When it is applicable, the Cholesky decomposition is roughly twice as efficient as the LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
for solving systems of linear equations. In a loose, metaphorical sense, this can be thought of as the matrix analogue of taking the square root of a number.
Statement
If A has real entries and is symmetric (or more generally, is Hermitian) and positive definite, then A can be decomposed aswhere L is a lower triangular matrix with strictly positive diagonal entries, and L* denotes the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of L. This is the Cholesky decomposition.
The Cholesky decomposition is unique: given a Hermitian, positive-definite matrix A, there is only one lower triangular matrix L with strictly positive diagonal entries such that A = LL*. The converse holds trivially: if A can be written as LL* for some invertible L, lower triangular or otherwise, then A is Hermitian and positive definite.
The requirement that L have strictly positive diagonal entries can be dropped to extend the factorization to the positive-semidefinite case. The statement then reads: a square matrix A has a Cholesky decomposition if and only if A is Hermitian and positive semi-definite. Cholesky factorizations for positive-semidefinite matrices are not unique in general.
In the special case that A is a symmetric positive-definite matrix with real entries, L has real entries as well.
Applications
The Cholesky decomposition is mainly used for the numerical solution of linear equations Ax = b. If A is symmetric and positive definite, then we can solve Ax = b by first computing the Cholesky decomposition A = LLT, then solving Ly = b for y, and finally solving LTx = y for x.Linear least squares
Systems of the form Ax = b with A symmetric and positive definite arise quite often in applications. For instance, the normal equations in linear least squaresLinear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
problems are of this form. It may also happen that matrix A comes from an energy functional which must be positive from physical considerations; this happens frequently in the numerical solution of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s.
Non-linear optimization
Non-linear multi-variate functions may be minimized over their parameters using variants of Newton's method called quasi-Newton methods. At each iteration, the search takes a step s defined by solving Hs = -g for s, where s is the step, g is the gradient vector of the function's partial first derivatives with respect to the parameters, and H is an approximation to the Hessian matrixHessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
of partial second derivatives formed by repeated rank 1 updates at each iteration. Two well-known update formulae are called Davidon-Fletcher-Powell (DFP) and Broydon-Fletcher-Goldfarb-Shanno (BFGS). Loss of the positive-definite condition through round-off error is avoided if rather than updating an approximation to the inverse of the Hessian, one updates the Cholesky decomposition of an approximation of the Hessian matrix itself.
Monte Carlo simulation
The Cholesky decomposition is commonly used in the Monte Carlo methodMonte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
for simulating systems with multiple correlated variables: The covariance matrix
Covariance matrix
In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
is decomposed, to give the lower-triangular L. Applying this to a vector of uncorrelated samples, u, produces a sample vector Lu with the covariance properties of the system being modeled.
Kalman filters
Unscented Kalman filterKalman filter
In statistics, the Kalman filter is a mathematical method named after Rudolf E. Kálmán. Its purpose is to use measurements observed over time, containing noise and other inaccuracies, and produce values that tend to be closer to the true values of the measurements and their associated calculated...
s commonly use the Cholesky decomposition to choose a set of so-called sigma points. The Kalman filter tracks the average state of a system as a vector x of length N and covariance as an N-by-N matrix P. The matrix P is always positive semi-definite, and can be decomposed into LLT. The columns of L can be added and subtracted from the mean x to form a set of 2N vectors called sigma points. These sigma points completely capture the mean and covariance of the system state.
Computing the Cholesky decomposition
There are various methods for calculating the Cholesky decomposition. The computational complexity of commonly used algorithms is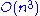 in general. The algorithms described below all involve about n3/3 FLOPFlop
- Terms :*Flop, a box office bomb in the entertainment world*Flop, as verb or noun, referring to flophouse, cheap rooms in a transients' hotel*Flop , a poker term describing the first three cards dealt to the board...
s, where n is the size of the matrix A. Hence, they are half the cost of the LU decomposition
LU decomposition
In linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
, which uses 2n3/3 FLOPs (see Trefethen and Bau 1997).
Which of the algorithms below is faster depends on the details of the implementation. Generally, the first algorithm will be slightly slower because it accesses the data in a more irregular manner.
The Cholesky algorithm
The Cholesky algorithm, used to calculate the decomposition matrix L, is a modified version of Gaussian eliminationGaussian elimination
In linear algebra, Gaussian elimination is an algorithm for solving systems of linear equations. It can also be used to find the rank of a matrix, to calculate the determinant of a matrix, and to calculate the inverse of an invertible square matrix...
.
The recursive algorithm starts with i := 1 and
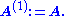
At step i, the matrix A(i) has the following form:
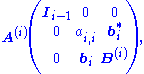
where Ii−1 denotes the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
of dimension i − 1.
If we now define the matrix Li by
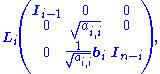
then we can write A(i) as
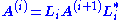
where
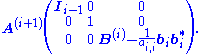
Note that bi bi* is an outer product
Outer product
In linear algebra, the outer product typically refers to the tensor product of two vectors. The result of applying the outer product to a pair of vectors is a matrix...
, therefore this algorithm is called the outer product version in (Golub & Van Loan).
We repeat this for i from 1 to n. After n steps, we get A(n+1) = I. Hence, the lower triangular matrix L we are looking for is calculated as
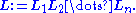
The Cholesky–Banachiewicz and Cholesky–Crout algorithms
If we write out the equation A = LL*,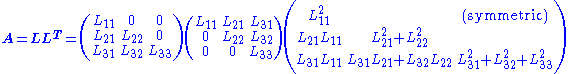we obtain the following formula for the entries of L:
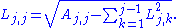
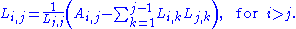
The expression under the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
is always positive if A is real and positive-definite.
For complex Hermitian matrix, the following formula applies:
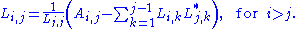
So we can compute the (i, j) entry if we know the entries to the left and above. The computation is usually arranged in either of the following orders.
- The Cholesky–Banachiewicz algorithm starts from the upper left corner of the matrix L and proceeds to calculate the matrix row by row.
- The Cholesky–Crout algorithm starts from the upper left corner of the matrix L and proceeds to calculate the matrix column by column.
Stability of the computation
Suppose that we want to solve a well-conditionedCondition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
system of linear equations. If the LU decomposition is used, then the algorithm is unstable unless we use some sort of pivoting strategy. In the latter case, the error depends on the so-called growth factor of the matrix, which is usually (but not always) small.
Now, suppose that the Cholesky decomposition is applicable. As mentioned above, the algorithm will be twice as fast. Furthermore, no pivoting is necessary and the error will always be small. Specifically, if we want to solve Ax = b, and y denotes the computed solution, then y solves the disturbed system (A + E)y = b where
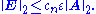
Here, || ||2 is the matrix 2-norm, cn is a small constant depending on n, and ε denotes the unit round-off.
There is one small problem with the Cholesky decomposition. Note that we must compute square roots in order to find the Cholesky decomposition. If the matrix is real symmetric and positive definite, then the numbers under the square roots are always positive in exact arithmetic. Unfortunately, the numbers can become negative because of round-off error
Round-off error
A round-off error, also called rounding error, is the difference between the calculated approximation of a number and its exact mathematical value. Numerical analysis specifically tries to estimate this error when using approximation equations and/or algorithms, especially when using finitely many...
s, in which case the algorithm cannot continue. However, this can only happen if the matrix is very ill-conditioned.
Avoiding taking square roots
An alternative form is the factorization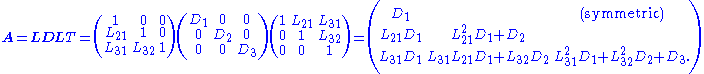This form eliminates the need to take square roots. When A is positive definite the elements of the diagonal matrix D are all positive. However this factorization may be used for most invertible symmetric matrices; an example of an invertible matrix whose decomposition is undefined is one where the first entry is zero.
If A is real, the following recursive relations apply for the entries of D and L:
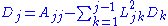
For complex Hermitian matrix A, the following formula applies:
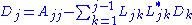
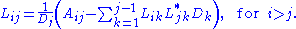
The LDLT and LLT factorizations (note that L is different between the two) may be easily related:
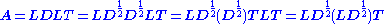
The last expression is the product of a lower triangular matrix and its transpose, as is the LLT factorization.
Proof for positive semi-definite matrices
The above algorithms show that every positive definite matrix A has a Cholesky decomposition. This result can be extended to the positive semi-definite case by a limiting argument. The argument is not fully constructive, i.e., it gives no explicit numerical algorithms for computing Cholesky factors.If A is an n-by-n positive semi-definite matrix, then the sequence {Ak} = {A + (1/k)In} consists of positive definite matrices. (This is an immediate consequence of, for example, the spectral mapping theorem for the polynomial functional calculus.) Also,
in operator norm
Operator norm
In mathematics, the operator norm is a means to measure the "size" of certain linear operators. Formally, it is a norm defined on the space of bounded linear operators between two given normed vector spaces.- Introduction and definition :...
. From the positive definite case, each Ak has Cholesky decomposition Ak = LkLk*. By property of the operator norm,
So {Lk} is a bounded set in the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
of operators, therefore relatively compact (because the underlying vector space is finite dimensional). Consequently it has a convergent subsequence, also denoted by {Lk}, with limit L. It can be easily checked that this L has the desired properties, i.e. A = LL* and L is lower triangular with non-negative diagonal entries: for all x and y,
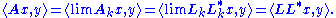
Therefore A = LL*. Because the underlying vector space is finite dimensional, all topologies on the space of operators are equivalent. So Lk tends to L in norm means Lk tends to L entrywise. This in turn implies that, since each Lk is lower triangular with non-negative diagonal entries, L is also.
Generalization
The Cholesky factorization can be generalized to (not necessarily finite) matrices with operator entries. Let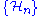 be a sequence of Hilbert spaces. Consider the operator matrix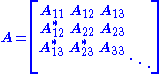acting on the direct sum
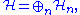
where each
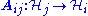
is a bounded operator
Bounded operator
In functional analysis, a branch of mathematics, a bounded linear operator is a linear transformation L between normed vector spaces X and Y for which the ratio of the norm of L to that of v is bounded by the same number, over all non-zero vectors v in X...
. If A is positive (semidefinite) in the sense that for all finite k and for any
we have
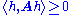, then there exists a lower triangular operator matrix L such that A = LL*. One can also take the diagonal entries of L to be positive.See also
- Symbolic Cholesky decompositionSymbolic Cholesky decompositionIn the mathematical subfield of numerical analysis the symbolic Cholesky decomposition is an algorithm used to determine the non-zero pattern for the L factors of a symmetric sparse matrix when applying the Cholesky decomposition or variants.-Algorithm:...
- Minimum degree algorithmMinimum degree algorithmIn numerical analysis the minimum degree algorithm is an algorithm used to permute the rows and columns of a symmetric sparse matrix before applying the Cholesky decomposition, to reduce the number of non-zeros in the Cholesky factor....
- Matrix decompositionMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
- Sylvester's law of inertiaSylvester's law of inertiaSylvester's law of inertia is a theorem in matrix algebra about certain properties of the coefficient matrix of a real quadratic form that remain invariant under a change of coordinates...
- Cycle rankCycle rankIn graph theory, the cycle rank of a directed graph is a digraph connectivity measure proposed first by Eggan and Büchi . Intuitively, this concept measures how close adigraph is to a directed acyclic graph , in the sense that a DAG has...
Information
- Cholesky Decomposition, The Data Analysis BriefBook
- Module for Cholesky Factorization
- Cholesky Decomposition on www.math-linux.com
Computer code
- LAPACK is a collection of FORTRAN subroutines for solving dense linear algebra problems
- ALGLIB includes a partial port of the LAPACK to C++, C#, Delphi, Visual Basic, etc.
- libflame is a C library with LAPACK functionality
- Notes and video on high-performance implementation of Cholesky factorization at The University of Texas at Austin.
- Cholesky : TBB + Threads + SSE is a book explaining the implementation of the CF with TBB,threads and SSE (in spanish)
Use of the matrix in simulation
- Simulation of correlated normal random variables
- Generating Correlated Random Variables, Martin Haugh, Columbia UniversityColumbia UniversityColumbia University in the City of New York is a private, Ivy League university in Manhattan, New York City. Columbia is the oldest institution of higher learning in the state of New York, the fifth oldest in the United States, and one of the country's nine Colonial Colleges founded before the...
Online calculators
- Online Matrix Calculator Performs Cholesky decomposition of matrices online.