
Elliptic boundary value problem
Encyclopedia
In mathematics
, an elliptic boundary value problem is a special kind of boundary value problem
which can be thought of as the stable state of an evolution problem. For example, the Dirichlet problem
for the Laplacian gives the eventual distribution of heat in a room several hours after the heating is turned on.
Differential equations describe a large class of natural phenomena, from the heat equation
describing the evolution of heat in (for instance) a metal plate, to the Navier-Stokes equation describing the movement of fluids, including Einstein's equations describing the physical universe in a relativistic way. Although all these equations are boundary value problems, they are further subdivided into categories. This is necessary because each category must be analyzed using different techniques. The present article deals with the category of boundary value problems known as linear elliptic problems.
Boundary value problems and partial differential equations specify relations between two or more quantities. For instance, in the heat equation, the rate of change of temperature at a point is related to the difference of temperature between that point and the nearby points so that, over time, the heat flows from hotter points to cooler points. Boundary value problems can involve space, time and other quantities such as temperature, velocity, pressure, magnetic field, etc...
Some problems do not involve time. For instance, if one hangs a clothesline between the house and a tree, then in the absence of wind, the clothesline will not move and will adopt a gentle hanging curved shape known as the catenary
. This curved shape can be computed as the solution of a differential equation relating position, tension, angle and gravity, but since the shape does not change over time, there is no time variable.
Elliptic boundary value problems are a class of problems which do not involve the time variable, and instead only depend on space variables.
It is not possible to discuss elliptic boundary value problems in more detail without referring to calculus
in multiple variables.
Unless otherwise noted, all facts presented in this article can be found in .
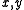 be the coordinates. We will use the notation
be the coordinates. We will use the notation 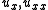 for the first and second partial derivative
for the first and second partial derivative
s of with respect to
with respect to  , and a similar notation for
, and a similar notation for 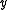 . We will use the symbols
. We will use the symbols 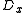 and
and  for the partial differential operators in
for the partial differential operators in  and
and 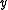 . The second partial derivatives will be denoted
. The second partial derivatives will be denoted 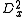 and
and 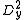 . We also define the gradient
. We also define the gradient 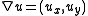 , the Laplace operator
, the Laplace operator
 and the divergence
and the divergence 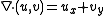 . Note from the definitions that
. Note from the definitions that 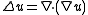 .
.
The main example for boundary value problems is the Laplace operator,

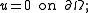
where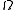 is a region in the plane and
is a region in the plane and 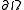 is the boundary of that region. The function
is the boundary of that region. The function  is known data and the solution
is known data and the solution  is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.
is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.
The solution can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like
can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like 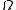 , if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary condition
, if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary condition
.) The function represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate
represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate  , which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach
, which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach  .
.
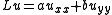 where
where  and
and 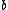 are constants.
are constants.  is called a second order differential operator
is called a second order differential operator
. If we formally replace the derivatives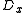 by
by  and
and 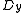 by
by 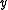 , we obtain the expression
, we obtain the expression
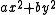 .
.
If we set this expression equal to some constant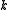 , then we obtain either an ellipse
, then we obtain either an ellipse
(if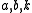 are all the same sign) or a hyperbola
are all the same sign) or a hyperbola
(if and
and  are of opposite signs.) For that reason,
are of opposite signs.) For that reason, 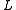 is said to be elliptic when
is said to be elliptic when 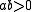 and hyperbolic if
and hyperbolic if 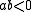 . Similarly, the operator
. Similarly, the operator 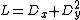 leads to a parabola
leads to a parabola
, and so this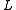 is said to be parabolic.
is said to be parabolic.
We now generalize the notion of ellipticity. While it may not be obvious that our generalization is the right one, it turns out that it does preserve most of the necessary properties for the purpose of analysis.
 be the space variables. Let
be the space variables. Let 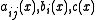 be real valued functions of
be real valued functions of 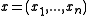 . Let
. Let 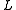 be a second degree linear operator. That is,
be a second degree linear operator. That is,
 (divergence form).
(divergence form). (nondivergence form)
(nondivergence form)
We have used the subscript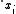 to denote the partial derivative
to denote the partial derivative
with respect to the space variable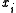 . The two formulae are equivalent, provided that
. The two formulae are equivalent, provided that
 .
.
In matrix notation, we can let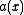 be an
be an 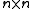 matrix valued function of
matrix valued function of  and
and 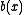 be a
be a  -dimensional column vector-valued function of
-dimensional column vector-valued function of  , and then we may write
, and then we may write
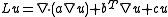 (divergence form).
(divergence form).
One may assume, without loss of generality, that the matrix is symmetric (that is, for all
is symmetric (that is, for all 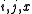 ,
, 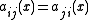 . We make that assumption in the rest of this article.
. We make that assumption in the rest of this article.
We say that the operator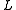 is elliptic if, for some constant
is elliptic if, for some constant  , any of the following equivalent conditions hold:
, any of the following equivalent conditions hold:
An elliptic boundary value problem is then a system of equations like
 (the PDE) and
(the PDE) and (the boundary value).
(the boundary value).
This particular example is the Dirichlet problem
. The Neumann problem is
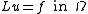 and
and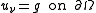
where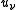 is the derivative of
is the derivative of  in the direction of the outwards pointing normal of
in the direction of the outwards pointing normal of 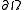 . In general, if
. In general, if 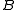 is any trace operator
is any trace operator
, one can construct the boundary value problem
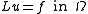 and
and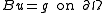 .
.
In the rest of this article, we assume that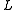 is elliptic and that the boundary condition is the Dirichlet condition
is elliptic and that the boundary condition is the Dirichlet condition 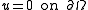 .
.
. We require the space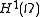 , the Sobolev space
, the Sobolev space
of "once-differentiable" functions on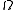 , such that both the function
, such that both the function  and its partial derivatives
and its partial derivatives 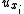 ,
,  are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space
are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space 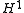 is a Hilbert space
is a Hilbert space
, which accounts for much of the ease with which these problems are analyzed.
The discussion in details of Sobolev spaces is beyond the scope of this article, but we will quote required results as they arise.
Unless otherwise noted, all derivatives in this article are to be interpreted in the weak, Sobolev sense. We use the term "strong derivative" to refer to the classical derivative of calculus. We also specify that the spaces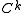 ,
, 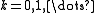 consist of functions that are
consist of functions that are 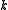 times strongly differentiable, and that the
times strongly differentiable, and that the 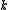 th derivative is continuous.
th derivative is continuous.
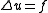 . Multiply each side of the equation by a "test function"
. Multiply each side of the equation by a "test function" 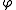 and integrate by parts using Green's theorem
and integrate by parts using Green's theorem
to obtain
 .
.
We will be solving the Dirichlet problem, so that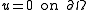 . For technical reasons, it is useful to assume that
. For technical reasons, it is useful to assume that 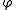 is taken from the same space of functions as
is taken from the same space of functions as  is so we also assume that
is so we also assume that 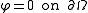 . This gets rid of the
. This gets rid of the 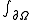 term, yielding
term, yielding
 (*)
(*)
where
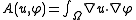 and
and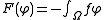 .
.
If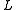 is a general elliptic operator, the same reasoning leads to the bilinear form
is a general elliptic operator, the same reasoning leads to the bilinear form
 .
.
We do not discuss the Neumann problem but note that it is analyzed in a similar way.
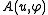 is defined on the Sobolev space
is defined on the Sobolev space  of functions which are once differentiable and zero on the boundary
of functions which are once differentiable and zero on the boundary 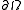 , provided we impose some conditions on
, provided we impose some conditions on 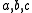 and
and 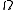 . There are many possible choices, but for the purpose of this article, we will assume that
. There are many possible choices, but for the purpose of this article, we will assume that
The reader may verify that the map is furthermore bilinear
is furthermore bilinear
and continuous
, and that the map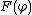 is linear
is linear
in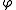 , and continuous if (for instance)
, and continuous if (for instance) 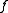 is square integrable.
is square integrable.
We say that the map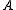 is coercive if there is an
is coercive if there is an 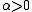 for all
for all  ,
,
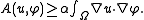
This is trivially true for the Laplacian (with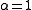 ) and is also true for an elliptic operator if we assume
) and is also true for an elliptic operator if we assume 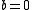 and
and 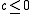 . (Recall that
. (Recall that 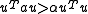 when
when  is elliptic.)
is elliptic.)
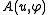 is coercive and
is coercive and 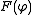 is continuous, then there exists a unique solution
is continuous, then there exists a unique solution 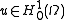 to the weak problem (*).
to the weak problem (*).
If further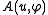 is symmetric (i.e.,
is symmetric (i.e.,  ), one can show the same result using the Riesz representation theorem
), one can show the same result using the Riesz representation theorem
instead.
This relies on the fact that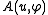 forms an inner product on
forms an inner product on 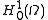 , which itself depends on Poincaré's inequality.
, which itself depends on Poincaré's inequality.
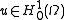 which solves the weak system, but we do not know if this
which solves the weak system, but we do not know if this  solves the strong system
solves the strong system
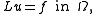
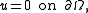
Even more vexing is that we are not even sure that is twice differentiable, rendering the expressions
is twice differentiable, rendering the expressions 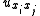 in
in 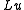 apparently meaningless. There are many ways to remedy the situation, the main one being regularity.
apparently meaningless. There are many ways to remedy the situation, the main one being regularity.
Theorem If (some condition), then the solution is in
is in 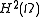 , the space of "twice differentiable" functions whose second derivatives are square integrable.
, the space of "twice differentiable" functions whose second derivatives are square integrable.
There is no known simple condition necessary and sufficient for the conclusion of the theorem to hold, but the following conditions are known to be sufficient:
It may be tempting to infer that if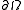 is piecewise
is piecewise  then
then  is indeed in
is indeed in 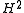 , but that is unfortunately false.
, but that is unfortunately false.
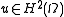 then the second derivatives of
then the second derivatives of  are defined almost everywhere
are defined almost everywhere
, and in that case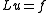 almost everywhere.
almost everywhere.
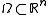 is a smooth manifold and
is a smooth manifold and 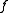 is infinitely differentiable in the strong sense, then
is infinitely differentiable in the strong sense, then  is also infinitely differentiable in the strong sense. In this case,
is also infinitely differentiable in the strong sense. In this case,  with the strong definition of the derivative.
with the strong definition of the derivative.
The proof of this relies upon an improved regularity theorem that says that if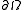 is
is 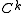 and
and 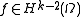 ,
, 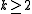 , then
, then 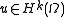 , together with a Sobolev imbedding theorem saying that functions in
, together with a Sobolev imbedding theorem saying that functions in  are also in
are also in 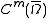 whenever
whenever 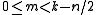 .
.
Because of the good properties we have enumerated (as well as many we have not), there are extremely efficient numerical solvers for linear elliptic boundary value problems (see finite element method
, finite difference method
and spectral method
for examples.)
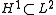 is a compact linear map. Equipped with the spectral theorem
is a compact linear map. Equipped with the spectral theorem
for compact linear operators, one obtains the following result.
Theorem Assume that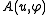 is coercive, continuous and symmetric. The map
is coercive, continuous and symmetric. The map 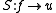 from
from 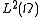 to
to 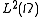 is a compact linear map. It has a basis
is a compact linear map. It has a basis
of eigenvectors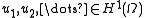 and matching eigenvalues
and matching eigenvalues 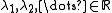 such that
such that
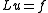 ,
,
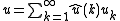
via the formula
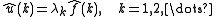
where
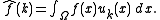
(See Fourier series
.)
The series converges in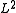 . Implemented on a computer using numerical approximations, this is known as the spectral method
. Implemented on a computer using numerical approximations, this is known as the spectral method
.
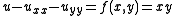 on
on 
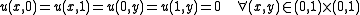 (Dirichlet conditions).
(Dirichlet conditions).
The reader may verify that the eigenvectors are exactly
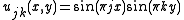 ,
, 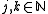
with eigenvalues
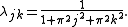
The Fourier coefficients of can be looked up in a table, getting
can be looked up in a table, getting 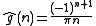 . Therefore,
. Therefore,
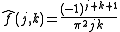
yielding the solution

Theorem. (Weak maximum principle.) Let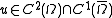 , and assume that
, and assume that 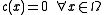 . Say that
. Say that  in
in 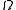 . Then
. Then 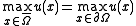 . In other words, the maximum is attained on the boundary.
. In other words, the maximum is attained on the boundary.
A strong maximum principle would conclude that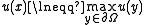 for all
for all 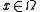 unless
unless  is constant.
is constant.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an elliptic boundary value problem is a special kind of boundary value problem
Boundary value problem
In mathematics, in the field of differential equations, a boundary value problem is a differential equation together with a set of additional restraints, called the boundary conditions...
which can be thought of as the stable state of an evolution problem. For example, the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
for the Laplacian gives the eventual distribution of heat in a room several hours after the heating is turned on.
Differential equations describe a large class of natural phenomena, from the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
describing the evolution of heat in (for instance) a metal plate, to the Navier-Stokes equation describing the movement of fluids, including Einstein's equations describing the physical universe in a relativistic way. Although all these equations are boundary value problems, they are further subdivided into categories. This is necessary because each category must be analyzed using different techniques. The present article deals with the category of boundary value problems known as linear elliptic problems.
Boundary value problems and partial differential equations specify relations between two or more quantities. For instance, in the heat equation, the rate of change of temperature at a point is related to the difference of temperature between that point and the nearby points so that, over time, the heat flows from hotter points to cooler points. Boundary value problems can involve space, time and other quantities such as temperature, velocity, pressure, magnetic field, etc...
Some problems do not involve time. For instance, if one hangs a clothesline between the house and a tree, then in the absence of wind, the clothesline will not move and will adopt a gentle hanging curved shape known as the catenary
Catenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
. This curved shape can be computed as the solution of a differential equation relating position, tension, angle and gravity, but since the shape does not change over time, there is no time variable.
Elliptic boundary value problems are a class of problems which do not involve the time variable, and instead only depend on space variables.
It is not possible to discuss elliptic boundary value problems in more detail without referring to calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
in multiple variables.
Unless otherwise noted, all facts presented in this article can be found in .
The main example
In two dimensions, let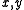 be the coordinates. We will use the notation
be the coordinates. We will use the notation 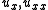 for the first and second partial derivative
for the first and second partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of
 with respect to
with respect to  , and a similar notation for
, and a similar notation for 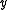 . We will use the symbols
. We will use the symbols 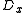 and
and  for the partial differential operators in
for the partial differential operators in  and
and 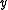 . The second partial derivatives will be denoted
. The second partial derivatives will be denoted 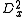 and
and 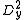 . We also define the gradient
. We also define the gradient 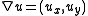 , the Laplace operator
, the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
 and the divergence
and the divergence 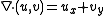 . Note from the definitions that
. Note from the definitions that 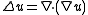 .
.The main example for boundary value problems is the Laplace operator,

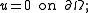
where
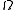 is a region in the plane and
is a region in the plane and  is the boundary of that region. The function
is the boundary of that region. The function  is known data and the solution
is known data and the solution  is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.
is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.The solution
 can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like
can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like 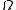 , if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary condition
, if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary conditionDirichlet boundary condition
In mathematics, the Dirichlet boundary condition is a type of boundary condition, named after Johann Peter Gustav Lejeune Dirichlet who studied under Cauchy and succeeded Gauss at University of Göttingen. When imposed on an ordinary or a partial differential equation, it specifies the values a...
.) The function
 represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate
represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate  , which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach
, which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach  .
.Nomenclature
Let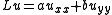 where
where  and
and 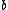 are constants.
are constants.  is called a second order differential operator
is called a second order differential operatorDifferential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
. If we formally replace the derivatives
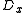 by
by  and
and 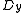 by
by 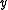 , we obtain the expression
, we obtain the expression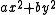 .
.If we set this expression equal to some constant
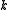 , then we obtain either an ellipse
, then we obtain either an ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
(if
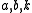 are all the same sign) or a hyperbola
are all the same sign) or a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
(if
 and
and  are of opposite signs.) For that reason,
are of opposite signs.) For that reason, 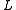 is said to be elliptic when
is said to be elliptic when 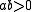 and hyperbolic if
and hyperbolic if 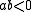 . Similarly, the operator
. Similarly, the operator 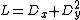 leads to a parabola
leads to a parabolaParabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, and so this
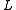 is said to be parabolic.
is said to be parabolic.We now generalize the notion of ellipticity. While it may not be obvious that our generalization is the right one, it turns out that it does preserve most of the necessary properties for the purpose of analysis.
General linear elliptic boundary value problems of the second degree
Let be the space variables. Let
be the space variables. Let 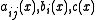 be real valued functions of
be real valued functions of 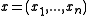 . Let
. Let 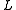 be a second degree linear operator. That is,
be a second degree linear operator. That is, (divergence form).
(divergence form). (nondivergence form)
(nondivergence form)We have used the subscript
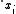 to denote the partial derivative
to denote the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
with respect to the space variable
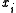 . The two formulae are equivalent, provided that
. The two formulae are equivalent, provided that .
.In matrix notation, we can let
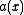 be an
be an 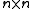 matrix valued function of
matrix valued function of  and
and 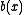 be a
be a  -dimensional column vector-valued function of
-dimensional column vector-valued function of  , and then we may write
, and then we may write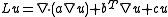 (divergence form).
(divergence form).One may assume, without loss of generality, that the matrix
 is symmetric (that is, for all
is symmetric (that is, for all 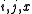 ,
, 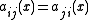 . We make that assumption in the rest of this article.
. We make that assumption in the rest of this article.We say that the operator
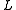 is elliptic if, for some constant
is elliptic if, for some constant  , any of the following equivalent conditions hold:
, any of the following equivalent conditions hold:-
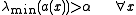 (see eigenvalue).
(see eigenvalue). -
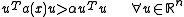 .
. -
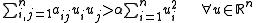 .
.
An elliptic boundary value problem is then a system of equations like
 (the PDE) and
(the PDE) and (the boundary value).
(the boundary value).This particular example is the Dirichlet problem
Dirichlet problem
In mathematics, a Dirichlet problem is the problem of finding a function which solves a specified partial differential equation in the interior of a given region that takes prescribed values on the boundary of the region....
. The Neumann problem is
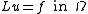 and
and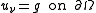
where
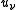 is the derivative of
is the derivative of  in the direction of the outwards pointing normal of
in the direction of the outwards pointing normal of 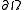 . In general, if
. In general, if 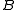 is any trace operator
is any trace operatorTrace operator
In mathematics, the concept of trace operator plays an important role in studying the existence and uniqueness of solutions to boundary value problems, that is, to partial differential equations with prescribed boundary conditions...
, one can construct the boundary value problem
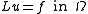 and
and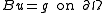 .
.In the rest of this article, we assume that
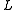 is elliptic and that the boundary condition is the Dirichlet condition
is elliptic and that the boundary condition is the Dirichlet condition 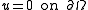 .
.Sobolev spaces
The analysis of elliptic boundary value problems requires some fairly sophisticated tools of functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. We require the space
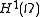 , the Sobolev space
, the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
of "once-differentiable" functions on
 , such that both the function
, such that both the function  and its partial derivatives
and its partial derivatives 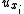 ,
, 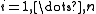 are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space
are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space 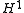 is a Hilbert space
is a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, which accounts for much of the ease with which these problems are analyzed.
The discussion in details of Sobolev spaces is beyond the scope of this article, but we will quote required results as they arise.
Unless otherwise noted, all derivatives in this article are to be interpreted in the weak, Sobolev sense. We use the term "strong derivative" to refer to the classical derivative of calculus. We also specify that the spaces
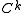 ,
, 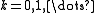 consist of functions that are
consist of functions that are 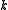 times strongly differentiable, and that the
times strongly differentiable, and that the 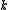 th derivative is continuous.
th derivative is continuous.Weak or variational formulation
The first step to cast the boundary value problem as in the language of Sobolev spaces is to rephrase it in its weak form. Consider the Laplace problem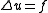 . Multiply each side of the equation by a "test function"
. Multiply each side of the equation by a "test function" 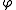 and integrate by parts using Green's theorem
and integrate by parts using Green's theoremGreen's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
to obtain
 .
.We will be solving the Dirichlet problem, so that
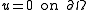 . For technical reasons, it is useful to assume that
. For technical reasons, it is useful to assume that 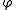 is taken from the same space of functions as
is taken from the same space of functions as  is so we also assume that
is so we also assume that 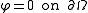 . This gets rid of the
. This gets rid of the 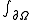 term, yielding
term, yielding (*)
(*)where
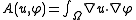 and
and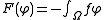 .
.If
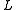 is a general elliptic operator, the same reasoning leads to the bilinear form
is a general elliptic operator, the same reasoning leads to the bilinear form .
.We do not discuss the Neumann problem but note that it is analyzed in a similar way.
Continuous and coercive bilinear forms
The map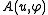 is defined on the Sobolev space
is defined on the Sobolev space  of functions which are once differentiable and zero on the boundary
of functions which are once differentiable and zero on the boundary 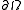 , provided we impose some conditions on
, provided we impose some conditions on 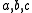 and
and 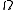 . There are many possible choices, but for the purpose of this article, we will assume that
. There are many possible choices, but for the purpose of this article, we will assume that-
 is continuously differentiable on
is continuously differentiable on  for
for 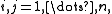
-
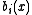 is continuous on
is continuous on 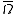 for
for 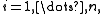
-
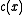 is continuous on
is continuous on 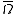 and
and -
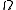 is bounded.
is bounded.
The reader may verify that the map
 is furthermore bilinear
is furthermore bilinearBilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
and continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
, and that the map
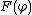 is linear
is linearLinear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
in
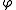 , and continuous if (for instance)
, and continuous if (for instance) 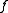 is square integrable.
is square integrable.We say that the map
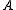 is coercive if there is an
is coercive if there is an 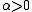 for all
for all  ,
,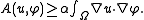
This is trivially true for the Laplacian (with
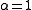 ) and is also true for an elliptic operator if we assume
) and is also true for an elliptic operator if we assume 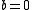 and
and 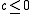 . (Recall that
. (Recall that 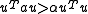 when
when  is elliptic.)
is elliptic.)Existence and uniqueness of the weak solution
One may show, via the Lax–Milgram lemma, that whenever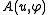 is coercive and
is coercive and 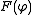 is continuous, then there exists a unique solution
is continuous, then there exists a unique solution 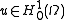 to the weak problem (*).
to the weak problem (*).If further
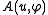 is symmetric (i.e.,
is symmetric (i.e.,  ), one can show the same result using the Riesz representation theorem
), one can show the same result using the Riesz representation theoremRiesz representation theorem
There are several well-known theorems in functional analysis known as the Riesz representation theorem. They are named in honour of Frigyes Riesz.- The Hilbert space representation theorem :...
instead.
This relies on the fact that
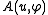 forms an inner product on
forms an inner product on 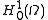 , which itself depends on Poincaré's inequality.
, which itself depends on Poincaré's inequality.Strong solutions
We have shown that there is a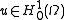 which solves the weak system, but we do not know if this
which solves the weak system, but we do not know if this  solves the strong system
solves the strong system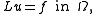
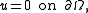
Even more vexing is that we are not even sure that
 is twice differentiable, rendering the expressions
is twice differentiable, rendering the expressions 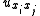 in
in 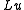 apparently meaningless. There are many ways to remedy the situation, the main one being regularity.
apparently meaningless. There are many ways to remedy the situation, the main one being regularity.Regularity
A regularity theorem for a linear elliptic boundary value problem of the second order takes the formTheorem If (some condition), then the solution
 is in
is in 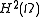 , the space of "twice differentiable" functions whose second derivatives are square integrable.
, the space of "twice differentiable" functions whose second derivatives are square integrable.There is no known simple condition necessary and sufficient for the conclusion of the theorem to hold, but the following conditions are known to be sufficient:
- The boundary of
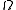 is
is 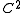 , or
, or -
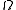 is convex.
is convex.
It may be tempting to infer that if
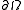 is piecewise
is piecewise  then
then  is indeed in
is indeed in 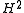 , but that is unfortunately false.
, but that is unfortunately false.Almost everywhere solutions
In the case that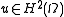 then the second derivatives of
then the second derivatives of  are defined almost everywhere
are defined almost everywhereAlmost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
, and in that case
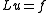 almost everywhere.
almost everywhere.Strong solutions
One may further prove that if the boundary of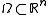 is a smooth manifold and
is a smooth manifold and 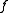 is infinitely differentiable in the strong sense, then
is infinitely differentiable in the strong sense, then  is also infinitely differentiable in the strong sense. In this case,
is also infinitely differentiable in the strong sense. In this case,  with the strong definition of the derivative.
with the strong definition of the derivative.The proof of this relies upon an improved regularity theorem that says that if
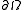 is
is 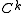 and
and 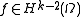 ,
, 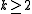 , then
, then 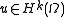 , together with a Sobolev imbedding theorem saying that functions in
, together with a Sobolev imbedding theorem saying that functions in  are also in
are also in 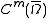 whenever
whenever 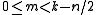 .
.Numerical solutions
While in exceptional circumstances, it is possible to solve elliptic problems explicitly, in general it is an impossible task. The natural solution is to approximate the elliptic problem with a simpler one and to solve this simpler problem on a computer.Because of the good properties we have enumerated (as well as many we have not), there are extremely efficient numerical solvers for linear elliptic boundary value problems (see finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
and spectral method
Spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
for examples.)
Eigenvalues and eigensolutions
Another Sobolev imbedding theorem states that the inclusion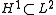 is a compact linear map. Equipped with the spectral theorem
is a compact linear map. Equipped with the spectral theoremSpectral theorem
In mathematics, particularly linear algebra and functional analysis, the spectral theorem is any of a number of results about linear operators or about matrices. In broad terms the spectral theorem provides conditions under which an operator or a matrix can be diagonalized...
for compact linear operators, one obtains the following result.
Theorem Assume that
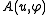 is coercive, continuous and symmetric. The map
is coercive, continuous and symmetric. The map 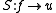 from
from 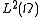 to
to 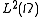 is a compact linear map. It has a basis
is a compact linear map. It has a basisBasis
Basis may refer to* Cost basis, in income tax law, the original cost of property adjusted for factors such as depreciation.* Basis of futures, the value differential between a future and the spot price...
of eigenvectors
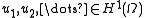 and matching eigenvalues
and matching eigenvalues 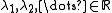 such that
such that-
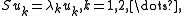
-
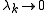 as
as 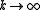 ,
, -
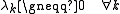 ,
, -
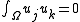 whenever
whenever 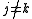 and
and -
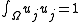 for all
for all 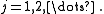
Series solutions and the importance of eigensolutions
If one has computed the eigenvalues and eigenvectors, then one may find the "explicit" solution of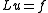 ,
,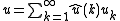
via the formula
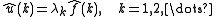
where
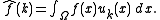
(See Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
.)
The series converges in
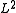 . Implemented on a computer using numerical approximations, this is known as the spectral method
. Implemented on a computer using numerical approximations, this is known as the spectral methodSpectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential...
.
An example
Consider the problem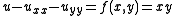 on
on 
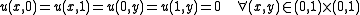 (Dirichlet conditions).
(Dirichlet conditions).The reader may verify that the eigenvectors are exactly
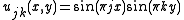 ,
, 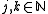
with eigenvalues
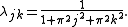
The Fourier coefficients of
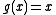 can be looked up in a table, getting
can be looked up in a table, getting 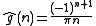 . Therefore,
. Therefore,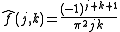
yielding the solution

Maximum principle
There are many variants of the maximum principle. We give a simple one.Theorem. (Weak maximum principle.) Let
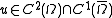 , and assume that
, and assume that 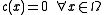 . Say that
. Say that  in
in 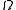 . Then
. Then 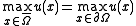 . In other words, the maximum is attained on the boundary.
. In other words, the maximum is attained on the boundary.A strong maximum principle would conclude that
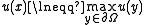 for all
for all 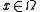 unless
unless  is constant.
is constant.

