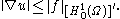Weak formulation
Encyclopedia
Weak formulations are an important tool for the analysis of mathematical equations that permit the transfer of concepts of linear algebra
to solve problems in other fields such as partial differential equation
s. In a weak formulation, an equation is no longer required to hold absolutely (and this is not even well defined) and has instead weak solution
s only with respect to certain "test vectors" or "test functions". This is equivalent to formulating the problem to require a solution in the sense of a distribution
.
We introduce weak formulations by a few examples and present the main theorem for the solution, the Lax–Milgram theorem.
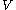 be a Banach space
be a Banach space
. We want to find the solution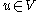 of the equation
of the equation
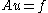 ,
,
where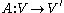 and
and 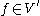 , and
, and 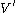 is the dual
is the dual
of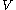 .
.
Calculus of variations
tells us that this is equivalent to finding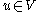 such that
such that
for all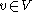 holds:
holds:
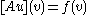 .
.
Here, we call a test vector or test function.
a test vector or test function.
We bring this into the generic form of a weak formulation, namely, find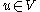 such that
such that
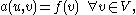
by defining the bilinear form
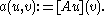
Since this is very abstract, let us follow this by some examples.
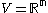 and
and 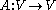 a linear mapping. Then, the weak formulation of the equation
a linear mapping. Then, the weak formulation of the equation
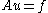
involves finding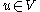 such that for all
such that for all 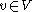 the following equation holds:
the following equation holds:
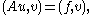
where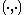 denotes an inner product.
denotes an inner product.
Since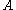 is a linear mapping, it is sufficient to test with basis vectors, we get
is a linear mapping, it is sufficient to test with basis vectors, we get
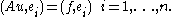
Actually, expanding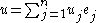 , we obtain the matrix form of the equation
, we obtain the matrix form of the equation
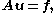
where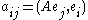 and
and 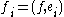 .
.
The bilinear form associated to this weak formulation is
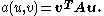
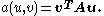
on a domain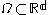 with
with 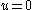 on its boundary,
on its boundary,
and we want to specify the solution space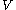 later. We will use the
later. We will use the 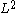 -scalar product
-scalar product
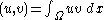
to derive our weak formulation. Then, testing with differentiable functions , we get
, we get
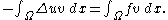
We can make the left side of this equation more symmetric by integration by parts
using Green's identity
:
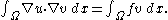
This is what is usually called the weak formulation of Poisson's equation
; what's missing is the space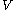 . Well, this is a bit tricky and way beyond the scope of this article. The space must allow us to write down this equation. Therefore, we should require that the derivatives of functions in this space are square integrable. Now, there is actually the Sobolev space
. Well, this is a bit tricky and way beyond the scope of this article. The space must allow us to write down this equation. Therefore, we should require that the derivatives of functions in this space are square integrable. Now, there is actually the Sobolev space
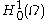 of functions with weak derivative
of functions with weak derivative
s in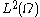 and with zero boundary conditions, which fulfills this purpose.
and with zero boundary conditions, which fulfills this purpose.
We obtain the generic form by assigning
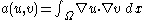
and
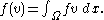
Let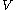 be a Hilbert space
be a Hilbert space
and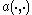 a bilinear form on
a bilinear form on 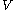 , which is
, which is
Then, for any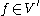 , there is a unique solution
, there is a unique solution 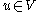 to the equation
to the equation
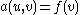
and it holds
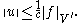
Additionally, we get the estimate
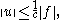
where is the minimal real part of an eigenvalue of
is the minimal real part of an eigenvalue of 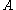 .
.
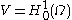 with the norm
with the norm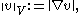
where the norm on the right is the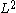 -norm on
-norm on 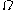 (this provides a true norm on
(this provides a true norm on 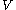 by the Poincaré inequality
by the Poincaré inequality
).
But, we see that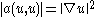 and by the Cauchy–Schwarz inequality
and by the Cauchy–Schwarz inequality
,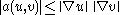 .
.
Therefore, for any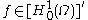 , there is a unique solution
, there is a unique solution 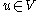 of Poisson's equation
of Poisson's equation
and we have the estimate
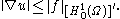
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
to solve problems in other fields such as partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s. In a weak formulation, an equation is no longer required to hold absolutely (and this is not even well defined) and has instead weak solution
Weak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
s only with respect to certain "test vectors" or "test functions". This is equivalent to formulating the problem to require a solution in the sense of a distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
.
We introduce weak formulations by a few examples and present the main theorem for the solution, the Lax–Milgram theorem.
General concept
Let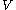 be a Banach space
be a Banach spaceBanach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
. We want to find the solution
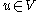 of the equation
of the equation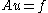 ,
,where
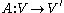 and
and 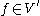 , and
, and 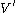 is the dual
is the dualDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of
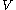 .
.Calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
tells us that this is equivalent to finding
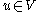 such that
such thatfor all
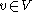 holds:
holds: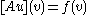 .
.Here, we call
 a test vector or test function.
a test vector or test function.We bring this into the generic form of a weak formulation, namely, find
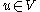 such that
such that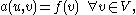
by defining the bilinear form
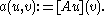
Since this is very abstract, let us follow this by some examples.
Example 1: linear system of equations
Now, let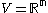 and
and 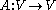 a linear mapping. Then, the weak formulation of the equation
a linear mapping. Then, the weak formulation of the equation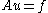
involves finding
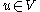 such that for all
such that for all 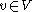 the following equation holds:
the following equation holds: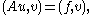
where
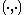 denotes an inner product.
denotes an inner product.Since
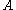 is a linear mapping, it is sufficient to test with basis vectors, we get
is a linear mapping, it is sufficient to test with basis vectors, we get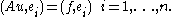
Actually, expanding
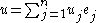 , we obtain the matrix form of the equation
, we obtain the matrix form of the equation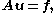
where
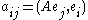 and
and 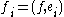 .
.The bilinear form associated to this weak formulation is
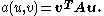
Example 2: Poisson's equation
Our aim is to solve Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
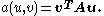
on a domain
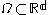 with
with 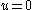 on its boundary,
on its boundary,and we want to specify the solution space
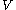 later. We will use the
later. We will use the 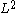 -scalar product
-scalar product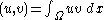
to derive our weak formulation. Then, testing with differentiable functions
 , we get
, we get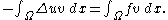
We can make the left side of this equation more symmetric by integration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
using Green's identity
Green's identities
In mathematics, Green's identities are a set of three identities in vector calculus. They are named after the mathematician George Green, who discovered Green's theorem.-Green's first identity:...
:
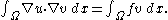
This is what is usually called the weak formulation of Poisson's equation
Poisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
; what's missing is the space
 . Well, this is a bit tricky and way beyond the scope of this article. The space must allow us to write down this equation. Therefore, we should require that the derivatives of functions in this space are square integrable. Now, there is actually the Sobolev space
. Well, this is a bit tricky and way beyond the scope of this article. The space must allow us to write down this equation. Therefore, we should require that the derivatives of functions in this space are square integrable. Now, there is actually the Sobolev spaceSobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
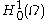 of functions with weak derivative
of functions with weak derivativeWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
s in
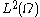 and with zero boundary conditions, which fulfills this purpose.
and with zero boundary conditions, which fulfills this purpose.We obtain the generic form by assigning
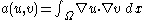
and
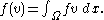
The Lax–Milgram theorem
This is a formulation of the Lax–Milgram theorem which relies on properties of the symmetric part of the bilinear form. It is not the most general form.Let
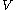 be a Hilbert space
be a Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
and
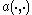 a bilinear form on
a bilinear form on 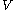 , which is
, which is- bounded:
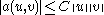 and
and
- coercive:
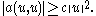
Then, for any
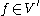 , there is a unique solution
, there is a unique solution 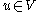 to the equation
to the equation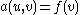
and it holds
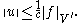
Application to example 1
Here, application of the Lax–Milgram theorem is definitely overkill, but we still can use it and give this problem the same structure as the others have.- Boundedness: all bilinear forms on
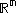 are bounded. In particular, we have
are bounded. In particular, we have

- Coercivity: this actually means that the real parts of the eigenvalues of
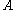 are not smaller than
are not smaller than  . Since this implies in particular that no eigenvalue is zero, the system is solvable.
. Since this implies in particular that no eigenvalue is zero, the system is solvable.
Additionally, we get the estimate
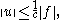
where
 is the minimal real part of an eigenvalue of
is the minimal real part of an eigenvalue of 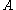 .
.Application to Example 2
Here, as we mentioned above, we choose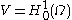 with the norm
with the norm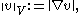
where the norm on the right is the
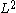 -norm on
-norm on 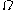 (this provides a true norm on
(this provides a true norm on 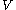 by the Poincaré inequality
by the Poincaré inequalityPoincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
).
But, we see that
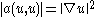 and by the Cauchy–Schwarz inequality
and by the Cauchy–Schwarz inequalityCauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
,
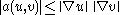 .
.Therefore, for any
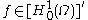 , there is a unique solution
, there is a unique solution 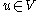 of Poisson's equation
of Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
and we have the estimate