
Binomial transform
Encyclopedia
In combinatorics
, the binomial transform is a sequence transformation (i.e., a transform of a sequence
) that computes its forward differences. It is closely related to the Euler transform, which is the result of applying the binomial transform to the sequence associated with its ordinary generating function.
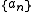 , is the sequence
, is the sequence  defined by
defined by
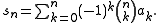
Formally, one may write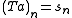 for the transformation, where T is an infinite-dimensional operator with matrix elements
for the transformation, where T is an infinite-dimensional operator with matrix elements 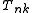 :
:
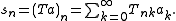
The transform is an involution, that is,
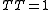
or, using index notation,
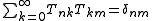
where δ is the Kronecker delta function. The original series can be regained by
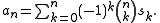
The binomial transform of a sequence is just the nth forward difference of the sequence, with odd differences carrying a negative sign, namely:


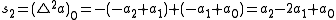
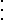
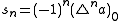
where Δ is the forward difference operator.
Some authors define the binomial transform with an extra sign, so that it is not self-inverse:
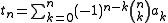
whose inverse is
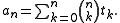
The top line 0, 1, 10, 63, 324, 1485,... (a sequence defined by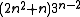 ) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by
) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by  ).
).
for the Bell number
s. That is,
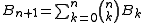
where the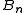 are the Bell numbers.
are the Bell numbers.
s associated with the series. For the ordinary generating function, let
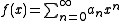
and
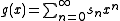
then
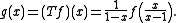
of an alternating series. That is, one has the identity

which is obtained by substituting x=1/2 into the last formula above. The terms on the right hand side typically become much smaller, much more rapidly, thus allowing rapid numerical summation.
The Euler transform can be generalized (Borisov B. and Shkodrov V., 2007):
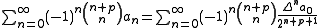 ,
,
where p = 0, 1, 2,...
The Euler transform is also frequently applied to the Euler hypergeometric integral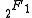 . Here, the Euler transform takes the form:
. Here, the Euler transform takes the form:
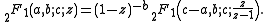
The binomial transform, and its variation as the Euler transform, is notable for its connection to the continued fraction
representation of a number. Let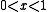 have the continued fraction representation
have the continued fraction representation
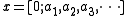
then
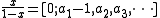
and
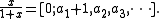

and
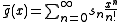
then
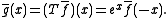
The Borel transform will convert the ordinary generating function to the exponential generating function.
transformation: letting
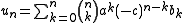
gives

where U and B are the ordinary generating functions associated with the series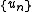 and
and 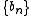 , respectively.
, respectively.
The rising k-binomial transform is sometimes defined as
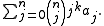
The falling k-binomial transform is
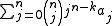 .
.
Both are homomorphisms of the kernel
of the Hankel transform of a series.
In the case where the binomial transform is defined as

Let this be equal to the function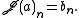
If a new forward difference table is made and the first elements from each row of this table are taken to form a new sequence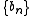 , then the second binomial transform of the original sequence is,
, then the second binomial transform of the original sequence is,

If the same process is repeated k times, then it follows that,
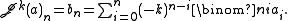
Its inverse is,

This can be generalized as,
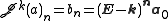
where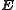 is the shift operator
is the shift operator
.
Its inverse is
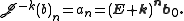
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, the binomial transform is a sequence transformation (i.e., a transform of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
) that computes its forward differences. It is closely related to the Euler transform, which is the result of applying the binomial transform to the sequence associated with its ordinary generating function.
Definition
The binomial transform, T, of a sequence,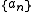 , is the sequence
, is the sequence  defined by
defined by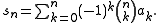
Formally, one may write
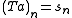 for the transformation, where T is an infinite-dimensional operator with matrix elements
for the transformation, where T is an infinite-dimensional operator with matrix elements 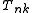 :
: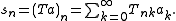
The transform is an involution, that is,
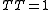
or, using index notation,
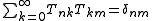
where δ is the Kronecker delta function. The original series can be regained by
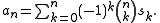
The binomial transform of a sequence is just the nth forward difference of the sequence, with odd differences carrying a negative sign, namely:


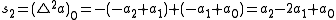
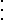
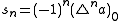
where Δ is the forward difference operator.
Some authors define the binomial transform with an extra sign, so that it is not self-inverse:
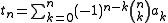
whose inverse is
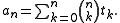
Example
Binomial transforms can be seen in difference tables. Consider the following:| 0 | 1 | 10 | 63 | 324 | 1485 | |||||
| 1 | 9 | 53 | 261 | 1161 | ||||||
| 8 | 44 | 208 | 900 | |||||||
| 36 | 164 | 692 | ||||||||
| 128 | 528 | |||||||||
| 400 |
The top line 0, 1, 10, 63, 324, 1485,... (a sequence defined by
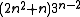 ) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by
) is the binomial transform of the diagonal 0, 1, 8, 36, 128, 400,... (a sequence defined by  ).
).Shift states
The binomial transform is the shift operatorShift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
for the Bell number
Bell number
In combinatorics, the nth Bell number, named after Eric Temple Bell, is the number of partitions of a set with n members, or equivalently, the number of equivalence relations on it...
s. That is,
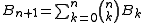
where the
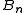 are the Bell numbers.
are the Bell numbers.Ordinary generating function
The transform connects the generating functionGenerating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s associated with the series. For the ordinary generating function, let
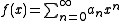
and
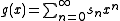
then
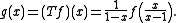
Euler transform
The relationship between the ordinary generating functions is sometimes called the Euler transform. It commonly makes its appearance in one of two different ways. In one form, it is used to accelerate the convergenceSeries acceleration
In mathematics, series acceleration is one of a collection of sequence transformations for improving the rate of convergence of a series. Techniques for series acceleration are often applied in numerical analysis, where they are used to improve the speed of numerical integration...
of an alternating series. That is, one has the identity

which is obtained by substituting x=1/2 into the last formula above. The terms on the right hand side typically become much smaller, much more rapidly, thus allowing rapid numerical summation.
The Euler transform can be generalized (Borisov B. and Shkodrov V., 2007):
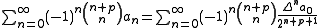 ,
,where p = 0, 1, 2,...
The Euler transform is also frequently applied to the Euler hypergeometric integral
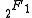 . Here, the Euler transform takes the form:
. Here, the Euler transform takes the form: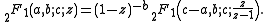
The binomial transform, and its variation as the Euler transform, is notable for its connection to the continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
representation of a number. Let
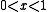 have the continued fraction representation
have the continued fraction representation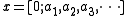
then
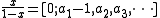
and
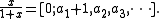
Exponential generating function
For the exponential generating function, let
and
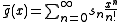
then
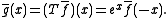
The Borel transform will convert the ordinary generating function to the exponential generating function.
Integral representation
When the sequence can be interpolated by a complex analytic function, then the binomial transform of the sequence can be represented by means of a Nörlund–Rice integral on the interpolating function.Generalizations
Prodinger gives a related, modular-likeModular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
transformation: letting
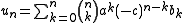
gives

where U and B are the ordinary generating functions associated with the series
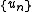 and
and 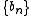 , respectively.
, respectively.The rising k-binomial transform is sometimes defined as
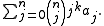
The falling k-binomial transform is
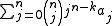 .
.Both are homomorphisms of the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the Hankel transform of a series.
In the case where the binomial transform is defined as

Let this be equal to the function
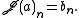
If a new forward difference table is made and the first elements from each row of this table are taken to form a new sequence
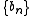 , then the second binomial transform of the original sequence is,
, then the second binomial transform of the original sequence is,
If the same process is repeated k times, then it follows that,
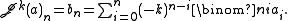
Its inverse is,

This can be generalized as,
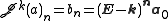
where
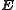 is the shift operator
is the shift operatorShift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
.
Its inverse is
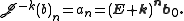
See also
- Newton series
- Hankel matrix
- Möbius transform
- Stirling transform
- Euler summationEuler summationEuler summation is a summability method for convergent and divergent series. Given a series Σan, if its Euler transform converges to a sum, then that sum is called the Euler sum of the original series....
- List of factorial and binomial topics

