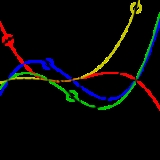
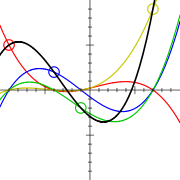
Lagrange polynomial
Encyclopedia
In numerical analysis
, Lagrange polynomials are used for polynomial interpolation
. For a given set of distinct points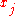
and numbers 
, the Lagrange polynomial is the polynomial of the least degree that at each point 
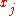assumes the corresponding value 
(i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of "the Lagrange form" of that unique polynomial rather than "the Lagrange interpolation polynomial," since the same polynomial can be arrived at through multiple methods. Although named after Joseph Louis Lagrange
, it was first discovered in 1779 by Edward Waring
and rediscovered in 1783 by Leonhard Euler
.
Lagrange interpolation is susceptible to Runge's phenomenon
, and the fact that changing the interpolation points requires recalculating the entire interpolant can make Newton polynomials easier to use. Lagrange polynomials are used in the Newton-Cotes method
of numerical integration and in Shamir's secret sharing scheme
in Cryptography.
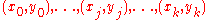
where no two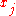
are the same, the interpolation polynomial in the Lagrange form is a linear combination
of Lagrange basis polynomials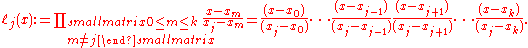
Note how, given the initial assumption that no two
are the same, 
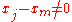, so this expression is always well-defined. The reason pairs 
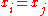with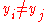 
are not allowed is that no interpolation function 
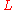such that 
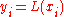would exist; a function can only get one value for each argument 
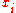. On the other hand, if also 
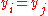, then those two points would actually be one single point.
For all
, 
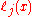includes the term 
in the numerator, so the whole product will be zero at 
:
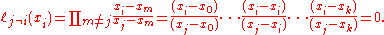
On the other hand,
In other words, all basis polynomials are zero at
, except 
, because it lacks the 
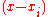term.
It follows that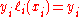
, so at each point 
, 
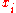, showing that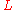 
interpolates the function exactly.
of the least degree that interpolates the given data set; that is, assumes value 
at the corresponding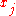 
for all data points 
:
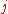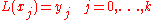
Observe that:
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, Lagrange polynomials are used for polynomial interpolation
Polynomial interpolation
In numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
. For a given set of distinct points
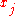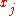and numbers , the Lagrange polynomial is the polynomial of the least degree that at each point assumes the corresponding value (i.e. the functions coincide at each point). The interpolating polynomial of the least degree is unique, however, and it is therefore more appropriate to speak of "the Lagrange form" of that unique polynomial rather than "the Lagrange interpolation polynomial," since the same polynomial can be arrived at through multiple methods. Although named after Joseph Louis LagrangeJoseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
, it was first discovered in 1779 by Edward Waring
Edward Waring
Edward Waring was an English mathematician who was born in Old Heath , Shropshire, England and died in Pontesbury, Shropshire, England. He entered Magdalene College, Cambridge as a sizar and became Senior wrangler in 1757. He was elected a Fellow of Magdalene and in 1760 Lucasian Professor of...
and rediscovered in 1783 by Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
.
Lagrange interpolation is susceptible to Runge's phenomenon
Runge's phenomenon
In the mathematical field of numerical analysis, Runge's phenomenon is a problem of oscillation at the edges of an interval that occurs when using polynomial interpolation with polynomials of high degree...
, and the fact that changing the interpolation points requires recalculating the entire interpolant can make Newton polynomials easier to use. Lagrange polynomials are used in the Newton-Cotes method
Newton-Cotes formulas
In numerical analysis, the Newton–Cotes formulae, also called the Newton–Cotes quadrature rules or simply Newton–Cotes rules, are a group of formulae for numerical integration based on evaluating the integrand at equally-spaced points...
of numerical integration and in Shamir's secret sharing scheme
Shamir's Secret Sharing
Shamir's Secret Sharing is an algorithm in cryptography. It is a form of secret sharing, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret....
in Cryptography.
Definition
Given a set of k + 1 data points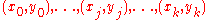where no two
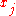are the same, the interpolation polynomial in the Lagrange form is a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of Lagrange basis polynomials
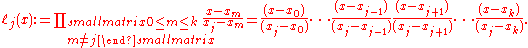
Note how, given the initial assumption that no two
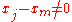are the same, , so this expression is always well-defined. The reason pairs 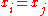with 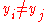are not allowed is that no interpolation function 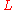such that 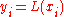would exist; a function can only get one value for each argument 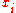. On the other hand, if also 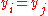, then those two points would actually be one single point.For all
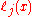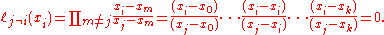
, includes the term in the numerator, so the whole product will be zero at :On the other hand,
In other words, all basis polynomials are zero at
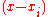, except , because it lacks the term.It follows that
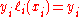, so at each poin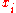t , , showing that 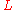interpolates the function exactly.Proof
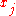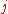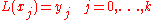
Function L(x) being sought is a polynomial in of the least degree that interpolates the given data set; that is, assumes value at the corresponding for all data points :Observe that:
- In
there are k terms in the product and each term contains one x, so L(x) (which is a sum of these k-degree polynomials) must also be a k-degree polynomial. -
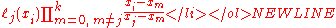
Watch what happens if we expand this product. Because the product skips
,
If
then all terms are 
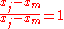(except where 
but that case is impossible as pointed out in the definition section---if you tried to write out that term you'd find that 
and since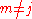 
, 
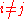, contrary to 
).
Also if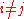
then since 
doesn't preclude it, one term in the product will be for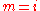 
, i.e. 
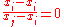, zeroing the entire product. So
-
where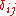
is the Kronecker delta. So:
Thus the function L(x) is a polynomial with degree at most k and where
.
Additionally, the interpolating polynomial is unique, as shown by the unisolvence theorem at Polynomial interpolationPolynomial interpolationIn numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
.
Main idea
Solving an interpolation problem leads to a problem in linear algebra where we have to solve a matrix. Using a standard monomial basisMonomial basisIn mathematics a monomial basis is a way to describe uniquely a polynomial using a linear combination of monomials. This description, the monomial form of a polynomial, is often used because of the simple structure of the monomial basis....
for our interpolation polynomial we get the Vandermonde matrix. By choosing another basis, the Lagrange basis, we get the much simpler identity matrixIdentity matrixIn linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
= δi,j which we can solve instantly: the Lagrange basis inverts the Vandermonde matrix.
This construction is the same as the Chinese Remainder TheoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
. Instead of checking for remainders of integers modulo prime numbers, we are checking for remainders of polynomials when divided by linears.
Example 1
Find an interpolation formula for ƒ(x) = tan(x) given this set of known values: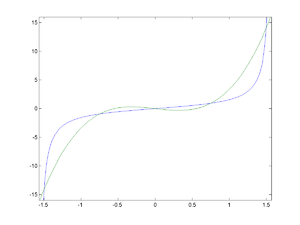
-
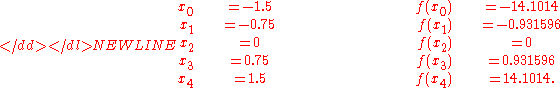
The basis polynomials are: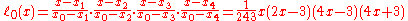
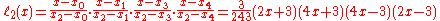
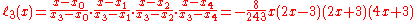
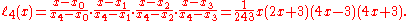
Thus the interpolating polynomial then is
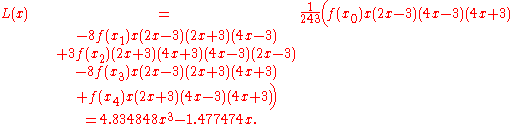
Example 2
We wish to interpolate ƒ(x) = x2 over the range 1 ≤ x ≤ 3, given these three points:
-
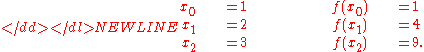
The interpolating polynomial is: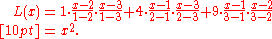
Example 3
We wish to interpolate ƒ(x) = x3 over the range 1 ≤ x ≤ 3, given these 3 points:
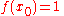
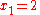
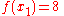
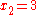
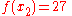
The interpolating polynomial is: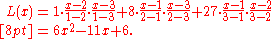
Barycentric interpolation
Using
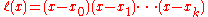
we can rewrite the Lagrange basis polynomials as
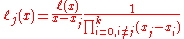
or, by defining the barycentric weights
we can simply write
which is commonly referred to as the first form of the barycentric interpolation formula.
The advantage of this representation is that the interpolation polynomial may now be evaluated as
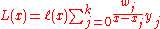
which, if the weights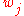
have been pre-computed, requires only 
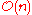operations (evaluating 
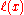and the weights 
) as opposed to 
for evaluating the Lagrange basis polynomials 
individually.
The barycentric interpolation formula can also easily be updated to incorporate a new node
by dividing each of the 
, 
by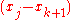 
and constructing the new 
as above.
We can further simplify the first form by first considering the barycentric interpolation of the constant function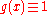
:
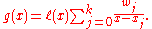
Dividing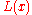
by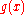 
does not modify the interpolation, yet yields
which is referred to as the second form or true form of the barycentric interpolation formula. This second form has the advantage that
need not be evaluated for each evaluation of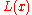 
.
Finite fields
The Lagrange polynomial can also be computed in finite fieldFinite fieldIn abstract algebra, a finite field or Galois field is a field that contains a finite number of elements. Finite fields are important in number theory, algebraic geometry, Galois theory, cryptography, and coding theory...
s. This has applications in cryptographyCryptographyCryptography is the practice and study of techniques for secure communication in the presence of third parties...
, such as in Shamir's Secret SharingShamir's Secret SharingShamir's Secret Sharing is an algorithm in cryptography. It is a form of secret sharing, where a secret is divided into parts, giving each participant its own unique part, where some of the parts or all of them are needed in order to reconstruct the secret....
scheme.
See also
- Polynomial interpolationPolynomial interpolationIn numerical analysis, polynomial interpolation is the interpolation of a given data set by a polynomial: given some points, find a polynomial which goes exactly through these points.- Applications :...
- Neville's algorithmNeville's algorithmIn mathematics, Neville's algorithm is an algorithm used for polynomial interpolation that was derived by the mathematician Eric Harold Neville. Given n + 1 points, there is a unique polynomial of degree ≤ n which goes through the given points...
- Newton formNewton polynomialIn the mathematical field of numerical analysis, a Newton polynomial, named after its inventor Isaac Newton, is the interpolation polynomial for a given set of data points in the Newton form...
of the interpolation polynomial - Bernstein formBernstein polynomialIn the mathematical field of numerical analysis, a Bernstein polynomial, named after Sergei Natanovich Bernstein, is a polynomial in the Bernstein form, that is a linear combination of Bernstein basis polynomials....
of the interpolation polynomial - Newton–Cotes formulas
- Lebesgue constant (interpolation)Lebesgue constant (interpolation)In mathematics, the Lebesgue constants give an idea of how good the interpolant of a function is in comparison with the best polynomial approximation of the function...
- The Chebfun systemChebfunChebfun is a freely available software system written in MATLAB for numerical computation with functions of a real variable. It is based on the idea of overloading MATLAB's commands for vectors and matrices to analogous commands for functions and operators...
External links
- ALGLIB has an implementations in C++ / C# / VBA / Pascal.
- GSL has a polynomial interpolation code in C
- Lagrange Method of Interpolation — Notes, PPT, Mathcad, Mathematica, MATLAB, Maple at Holistic Numerical Methods Institute
- Lagrange interpolation polynomial on www.math-linux.com
- Estimate of the error in Lagrange Polynomial Approximation at ProofWiki
- Module for Lagrange Polynomials by John H. Mathews
- Dynamic Lagrange interpolation with JSXGraph
- Numerical computing with functions: The Chebfun Project
- Polynomial interpolation
-
-
-