
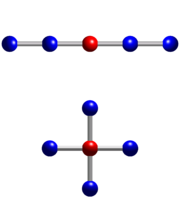
Five-point stencil
Encyclopedia
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, given a square grid in one or two dimensions, the five-point stencil of a point in the grid is made up of the point itself together with its four "neighbors". It is used to write finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
approximations to derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s at grid points.
One dimension
In one dimension, if the spacing between points in the grid is h, then the five-point stencil of a point x in the grid is
First derivative
The first derivative of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
ƒ of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variable at a point x can be approximated using a five-point stencil as
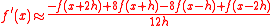
Obtaining the formula
This formula can be obtained by writing out the four Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of ƒ(x ± h) and ƒ(x ± 2h) up to terms of h 3 (or up to terms of h 5 to get an error estimation as well) and solving this system of four equations to get ƒ ′(x). Actually, we have at points x + h and x − h:

Evaluating (E 1+) − (E 1−) gives us
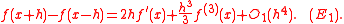
Note that the residual term O1(h 4) should be of the order of h 5 instead of h 4 because if the terms of h 4 had been written out in (E 1+) and (E 1−), it can be seen that they would have canceled each other out by ƒ(x + h) − ƒ(x − h). But for this calculation, it is left like that since the order of error estimation is not treated here (cf below).
Similarly, we have

and
 gives us
gives us
In order to eliminate the terms of ƒ (3)(x), calculate 8 × (E1) − (E2)

thus giving the formula as above.
Estimated error
The error in this approximation is of order h 4. That can be seen from the expansion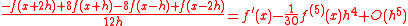
which can be obtained by expanding the left-hand side in a Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
. Alternatively, apply Richardson extrapolation
Richardson extrapolation
In numerical analysis, Richardson extrapolation is a sequence acceleration method, used to improve the rate of convergence of a sequence. It is named after Lewis Fry Richardson, who introduced the technique in the early 20th century. In the words of Birkhoff and Rota, ".....
to the central difference approximation to
 on grids with spacing 2h and h.
on grids with spacing 2h and h.Higher derivatives
The centered difference formulas for five-point stencils approximating second, third, and fourth derivatives are
Estimated errors
The errors in these approximations are O(h 4), O(h 2) and O(h 2) respectively.Relationship to Lagrange interpolating polynomials
As an alternative to deriving the finite difference weights from the Taylor series, they may be obtained by differentiating the Lagrange polynomialLagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
s

where the interpolation points are

Then, the quartic polynomial
 interpolating ƒ(x) at these five points is
interpolating ƒ(x) at these five points is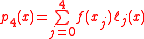
and its derivative is

So, the finite difference approximation of ƒ ′(x) at the middle point x = x2 is

Evaluating the derivatives of the five Lagrange polynomials at x=x2 gives the same weights as above. This method can be more flexible as the extension to a non-uniform grid is quite straightforward.
Two dimensions
In two dimensions, if for example the size of the squares in the grid is h by h, the five point stencil of a point (x, y) in the grid is
forming a pattern that is also called a quincunx
Quincunx
A quincunx is a geometric pattern consisting of five points arranged in a cross, that is five coplanar points, four of them forming a square or rectangle and a fifth at its center...
. This stencil is often used to approximate the Laplacian of a function of two variables:

The error in this approximation is O(h 2) , which may be explained as follows:
From the 3 point stencils for the second derivative of a function with respect to x and y:
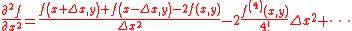
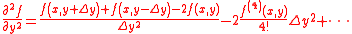
If we assume
 :
: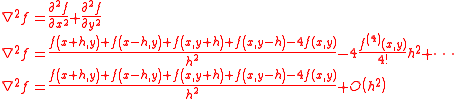
See also
- Stencil (numerical analysis)Stencil (numerical analysis)In mathematics, especially the areas of numerical analysis concentrating on the numerical solution of partial differential equations, a stencil is a geometric arrangement of a nodal group that relate to the point of interest by using a numerical approximation routine. Stencils are the basis for...
- Stencil jumpingStencil jumpingStencil jumping, at times called stencil walking, is an algorithm to locate the grid element enclosing a given point for any structured mesh...
- Finite difference coefficients

