
Fluid mechanics
Encyclopedia
Fluid mechanics is the study of fluid
s and the force
s on them. (Fluids include liquid
s, gas
es, and plasma
s.) Fluid mechanics can be divided into fluid statics
, the study of fluids at rest; fluid kinematics
, the study of fluids in motion; and fluid dynamics
, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics
, a subject which models matter without using the information that it is made out of atoms, that is, it models matter from a macroscopic viewpoint rather than from a microscopic viewpoint. Fluid mechanics, especially fluid dynamics, is an active field of research with many unsolved or partly solved problems. Fluid mechanics can be mathematically complex. Sometimes it can best be solved by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics
(CFD), is devoted to this approach to solving fluid mechanics problems. Also taking advantage of the highly visual nature of fluid flow is particle image velocimetry
, an experimental method for visualizing and analyzing fluid flow.
, when Archimedes
investigated fluid statics and buoyancy
and formulated his famous law known now as the Archimedes' Principle
. Rapid advancement in fluid mechanics began with Leonardo da Vinci
(observation and experiment), Evangelista Torricelli
(barometer
), Isaac Newton
(viscosity
) and Blaise Pascal
(hydrostatics), and was continued by Daniel Bernoulli
with the introduction of mathematical fluid dynamics in Hydrodynamica (1738). Inviscid flow was further analyzed by various mathematicians (Leonhard Euler
, d'Alembert, Lagrange
, Laplace, Poisson) and viscous flow was explored by a multitude of engineers including Poiseuille and Gotthilf Heinrich Ludwig Hagen
. Further mathematical justification was provided by Claude-Louis Navier
and George Gabriel Stokes
in the Navier–Stokes equations, and boundary layers were investigated (Ludwig Prandtl, Theodore von Kármán
), while various scientists (Osborne Reynolds
, Andrey Kolmogorov
, Geoffrey Ingram Taylor
) advanced the understanding of fluid viscosity and turbulence
.
, as illustrated in the following table.
In a mechanical view, a fluid is a substance that does not support shear stress
; that is why a fluid at rest has the shape of its containing vessel. A fluid at rest has no shear stress.
over the surface.
Fluid mechanics assumes that every fluid obeys the following:
Further, it is often useful (at subsonic
conditions) to assume a fluid is incompressible – that is, the density of the fluid does not change.
Similarly, it can sometimes be assumed that the viscosity
of the fluid is zero (the fluid is inviscid). Gases can often be assumed to be inviscid. If a fluid is viscous, and its flow contained in some way (e.g. in a pipe
), then the flow at the boundary must have zero velocity. For a viscous fluid, if the boundary is not porous, the shear forces between the fluid and the boundary results also in a zero velocity for the fluid at the boundary. This is called the no-slip condition
. For a porous media otherwise, in the frontier of the containing vessel, the slip condition is not zero velocity, and the fluid has a discontinuous velocity field between the free fluid and the fluid in the porous media (this is related to the Beavers and Joseph condition).
. That is, properties such as density, pressure, temperature, and velocity are taken to be well-defined at "infinitely" small points, defining a REV (Reference Element of Volume), at the geometric order of the distance between two adjacent molecules of fluid. Properties are assumed to vary continuously from one point to another, and are averaged values in the REV. The fact that the fluid is made up of discrete molecules is ignored.
The continuum hypothesis is basically an approximation, in the same way planets are approximated by point particles when dealing with celestial mechanics, and therefore results in approximate solutions. Consequently, assumption of the continuum hypothesis can lead to results which are not of desired accuracy. That said, under the right circumstances, the continuum hypothesis produces extremely accurate results.
Those problems for which the continuum hypothesis does not allow solutions of desired accuracy are solved using statistical mechanics
. To determine whether or not to use conventional fluid dynamics or statistical mechanics, the Knudsen number
is evaluated for the problem. The Knudsen number is defined as the ratio of the molecular mean free path
length to a certain representative physical length scale
. This length scale could be, for example, the radius of a body in a fluid. (More simply, the Knudsen number is how many times its own diameter a particle will travel on average before hitting another particle). Problems with Knudsen numbers at or above unity are best evaluated using statistical mechanics for reliable solutions.
and George Gabriel Stokes
) are the set of equations that describe the motion of fluid
substances such as liquids and gases. These equations state that changes in momentum
(force
) of fluid particles depend only on the external pressure
and internal viscous forces (similar to friction
) acting on the fluid. Thus, the Navier–Stokes equations describe the balance of forces acting at any given region of the fluid.
The Navier–Stokes equations are differential equations which describe the motion of a fluid. Such equations establish relations among the rates of change of the variables of interest. For example, the Navier–Stokes equations for an ideal fluid with zero viscosity states that acceleration (the rate of change of velocity) is proportional to the derivative of internal pressure.
This means that solutions of the Navier–Stokes equations for a given physical problem must be sought with the help of calculus
. In practical terms only the simplest cases can be solved exactly in this way. These cases generally involve non-turbulent, steady flow (flow does not change with time) in which the Reynolds number is small.
For more complex situations, such as global weather systems like El Niño or lift in a wing, solutions of the Navier–Stokes equations can currently only be found with the help of computers. This is a field of sciences by its own called computational fluid dynamics
.

where
Unless the fluid is made up of spinning degrees of freedom like vortices, is a symmetric tensor. In general, (in three dimensions)
is a symmetric tensor. In general, (in three dimensions)  has the form:
has the form:

where
The above is actually a set of three equations, one per dimension. By themselves, these aren't sufficient to produce a solution. However, adding conservation of mass and appropriate boundary conditions to the system of equations produces a solvable set of equations.
) is defined to be a fluid
whose shear stress
is linearly proportional to the velocity
gradient
in the direction perpendicular
to the plane of shear. This definition means regardless of the forces acting on a fluid, it continues to flow. For example, water is a Newtonian fluid, because it continues to display fluid properties no matter how much it is stirred or mixed. A slightly less rigorous definition is that the drag
of a small object being moved slowly through the fluid is proportional to the force applied to the object. (Compare friction
). Important fluids, like water as well as most gases, behave — to good approximation — as a Newtonian fluid under normal conditions on Earth.
By contrast, stirring a non-Newtonian fluid
can leave a "hole" behind. This will gradually fill up over time – this behaviour is seen in materials such as pudding, oobleck, or sand
(although sand isn't strictly a fluid). Alternatively, stirring a non-Newtonian fluid can cause the viscosity to decrease, so the fluid appears "thinner" (this is seen in non-drip paint
s). There are many types of non-Newtonian fluids, as they are defined to be something that fails to obey a particular property — for example, most fluids with long molecular chains can react in a non-Newtonian manner.
. A simple equation to describe Newtonian fluid behaviour is

where is the shear stress exerted by the fluid ("drag
is the shear stress exerted by the fluid ("drag
") is the fluid viscosity – a constant of proportionality
is the fluid viscosity – a constant of proportionality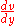 is the velocity gradient perpendicular to the direction of shear.
is the velocity gradient perpendicular to the direction of shear.
For a Newtonian fluid, the viscosity, by definition, depends only on temperature
and pressure
, not on the forces acting upon it. If the fluid is incompressible and viscosity is constant across the fluid, the equation governing the shear stress (in Cartesian coordinates
) is
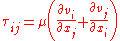
where is the shear stress on the
is the shear stress on the  face of a fluid element in the
face of a fluid element in the 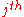 direction
direction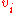 is the velocity in the
is the velocity in the  direction
direction is the
is the  direction coordinate.
direction coordinate.
If a fluid does not obey this relation, it is termed a non-Newtonian fluid
, of which there are several types.
Among fluids, two rough broad divisions can be made: ideal and non-ideal fluids. An ideal fluid really does not exist, but in some calculations, the assumption is justifiable. An Ideal fluid is non viscous- offers no resistance whatsoever to a shearing force.
One can group real fluids into Newtonian and non-Newtonian. Newtonian fluids agree with Newton's law of viscosity. Non-Newtonian fluids can be either plastic, bingham plastic, pseudoplastic, dilatant, thixotropic, rheopectic, viscoelatic.
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
s and the force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s on them. (Fluids include liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
s, gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
es, and plasma
Plasma (physics)
In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...
s.) Fluid mechanics can be divided into fluid statics
Fluid statics
Fluid statics is the science of fluids at rest, and is a sub-field within fluid mechanics. The term usually refers to the mathematical treatment of the subject. It embraces the study of the conditions under which fluids are at rest in stable equilibrium...
, the study of fluids at rest; fluid kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
, the study of fluids in motion; and fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, the study of the effect of forces on fluid motion. It is a branch of continuum mechanics
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, a subject which models matter without using the information that it is made out of atoms, that is, it models matter from a macroscopic viewpoint rather than from a microscopic viewpoint. Fluid mechanics, especially fluid dynamics, is an active field of research with many unsolved or partly solved problems. Fluid mechanics can be mathematically complex. Sometimes it can best be solved by numerical methods, typically using computers. A modern discipline, called computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
(CFD), is devoted to this approach to solving fluid mechanics problems. Also taking advantage of the highly visual nature of fluid flow is particle image velocimetry
Particle image velocimetry
Particle image velocimetry is an optical method of flow visualization used in education and research. It is used to obtain instantaneous velocity measurements and related properties in fluids...
, an experimental method for visualizing and analyzing fluid flow.
Brief history
The study of fluid mechanics goes back at least to the days of ancient GreeceAncient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
, when Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
investigated fluid statics and buoyancy
Buoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
and formulated his famous law known now as the Archimedes' Principle
Archimedes' principle
Archimedes' principle relates buoyancy to displacement. It is named after its discoverer, Archimedes of Syracuse.-Principle:Archimedes' treatise On floating bodies, proposition 5, states that...
. Rapid advancement in fluid mechanics began with Leonardo da Vinci
Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
(observation and experiment), Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
(barometer
Barometer
A barometer is a scientific instrument used in meteorology to measure atmospheric pressure. Pressure tendency can forecast short term changes in the weather...
), Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
(viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
) and Blaise Pascal
Blaise Pascal
Blaise Pascal , was a French mathematician, physicist, inventor, writer and Catholic philosopher. He was a child prodigy who was educated by his father, a tax collector in Rouen...
(hydrostatics), and was continued by Daniel Bernoulli
Daniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
with the introduction of mathematical fluid dynamics in Hydrodynamica (1738). Inviscid flow was further analyzed by various mathematicians (Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
, d'Alembert, Lagrange
Lagrange
La Grange literally means the barn in French. Lagrange may refer to:- People :* Charles Varlet de La Grange , French actor* Georges Lagrange , translator to and writer in Esperanto...
, Laplace, Poisson) and viscous flow was explored by a multitude of engineers including Poiseuille and Gotthilf Heinrich Ludwig Hagen
Gotthilf Heinrich Ludwig Hagen
Gotthilf Heinrich Ludwig Hagen was a German physicist and hydraulic engineer.Hagen was born in Königsberg, East Prussia . He studied mathematics, architecture, and civil engineering at the University of Königsberg...
. Further mathematical justification was provided by Claude-Louis Navier
Claude-Louis Navier
Claude-Louis Navier born Claude Louis Marie Henri Navier , was a French engineer and physicist who specialized in mechanics.The Navier–Stokes equations are named after him and George Gabriel Stokes....
and George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
in the Navier–Stokes equations, and boundary layers were investigated (Ludwig Prandtl, Theodore von Kármán
Theodore von Karman
Theodore von Kármán was a Hungarian-American mathematician, aerospace engineer and physicist who was active primarily in the fields of aeronautics and astronautics. He is responsible for many key advances in aerodynamics, notably his work on supersonic and hypersonic airflow characterization...
), while various scientists (Osborne Reynolds
Osborne Reynolds
Osborne Reynolds FRS was a prominent innovator in the understanding of fluid dynamics. Separately, his studies of heat transfer between solids and fluids brought improvements in boiler and condenser design.-Life:...
, Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, Geoffrey Ingram Taylor
Geoffrey Ingram Taylor
Sir Geoffrey Ingram Taylor OM was a British physicist, mathematician and expert on fluid dynamics and wave theory. His biographer and one-time student, George Batchelor, described him as "one of the most notable scientists of this century".-Biography:Taylor was born in St. John's Wood, London...
) advanced the understanding of fluid viscosity and turbulence
Turbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
.
Relationship to continuum mechanics
Fluid mechanics is a subdiscipline of continuum mechanicsContinuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
, as illustrated in the following table.
In a mechanical view, a fluid is a substance that does not support shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
; that is why a fluid at rest has the shape of its containing vessel. A fluid at rest has no shear stress.
Assumptions
Like any mathematical model of the real world, fluid mechanics makes some basic assumptions about the materials being studied. These assumptions are turned into equations that must be satisfied if the assumptions are to be held true. For example, consider an incompressible fluid in three dimensions. The assumption that mass is conserved means that for any fixed closed surface (such as a sphere) the rate of mass passing from outside to inside the surface must be the same as rate of mass passing the other way. (Alternatively, the mass inside remains constant, as does the mass outside). This can be turned into an integral equationIntegral equation
In mathematics, an integral equation is an equation in which an unknown function appears under an integral sign. There is a close connection between differential and integral equations, and some problems may be formulated either way...
over the surface.
Fluid mechanics assumes that every fluid obeys the following:
- Conservation of massConservation of massThe law of conservation of mass, also known as the principle of mass/matter conservation, states that the mass of an isolated system will remain constant over time...
- Conservation of energyConservation of energyThe nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...
- Conservation of momentum
- The continuum hypothesis, detailed below.
Further, it is often useful (at subsonic
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
conditions) to assume a fluid is incompressible – that is, the density of the fluid does not change.
Similarly, it can sometimes be assumed that the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
of the fluid is zero (the fluid is inviscid). Gases can often be assumed to be inviscid. If a fluid is viscous, and its flow contained in some way (e.g. in a pipe
Pipe (material)
A pipe is a tubular section or hollow cylinder, usually but not necessarily of circular cross-section, used mainly to convey substances which can flow — liquids and gases , slurries, powders, masses of small solids...
), then the flow at the boundary must have zero velocity. For a viscous fluid, if the boundary is not porous, the shear forces between the fluid and the boundary results also in a zero velocity for the fluid at the boundary. This is called the no-slip condition
No-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
. For a porous media otherwise, in the frontier of the containing vessel, the slip condition is not zero velocity, and the fluid has a discontinuous velocity field between the free fluid and the fluid in the porous media (this is related to the Beavers and Joseph condition).
The continuum hypothesis
Fluids are composed of molecules that collide with one another and solid objects. The continuum assumption, however, considers fluids to be continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. That is, properties such as density, pressure, temperature, and velocity are taken to be well-defined at "infinitely" small points, defining a REV (Reference Element of Volume), at the geometric order of the distance between two adjacent molecules of fluid. Properties are assumed to vary continuously from one point to another, and are averaged values in the REV. The fact that the fluid is made up of discrete molecules is ignored.
The continuum hypothesis is basically an approximation, in the same way planets are approximated by point particles when dealing with celestial mechanics, and therefore results in approximate solutions. Consequently, assumption of the continuum hypothesis can lead to results which are not of desired accuracy. That said, under the right circumstances, the continuum hypothesis produces extremely accurate results.
Those problems for which the continuum hypothesis does not allow solutions of desired accuracy are solved using statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
. To determine whether or not to use conventional fluid dynamics or statistical mechanics, the Knudsen number
Knudsen number
The Knudsen number is a dimensionless number defined as the ratio of the molecular mean free path length to a representative physical length scale. This length scale could be, for example, the radius of a body in a fluid...
is evaluated for the problem. The Knudsen number is defined as the ratio of the molecular mean free path
Mean free path
In physics, the mean free path is the average distance covered by a moving particle between successive impacts which modify its direction or energy or other particle properties.-Derivation:...
length to a certain representative physical length scale
Scale (ratio)
The scale ratio of some sort of model which represents an original proportionally is the ratio of a linear dimension of the model to the same dimension of the original. Examples include a 3-dimensional scale model of a building or the scale drawings of the elevations or plans of a building. In such...
. This length scale could be, for example, the radius of a body in a fluid. (More simply, the Knudsen number is how many times its own diameter a particle will travel on average before hitting another particle). Problems with Knudsen numbers at or above unity are best evaluated using statistical mechanics for reliable solutions.
Navier–Stokes equations
The Navier–Stokes equations (named after Claude-Louis NavierClaude-Louis Navier
Claude-Louis Navier born Claude Louis Marie Henri Navier , was a French engineer and physicist who specialized in mechanics.The Navier–Stokes equations are named after him and George Gabriel Stokes....
and George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
) are the set of equations that describe the motion of fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
substances such as liquids and gases. These equations state that changes in momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
(force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
) of fluid particles depend only on the external pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
and internal viscous forces (similar to friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
) acting on the fluid. Thus, the Navier–Stokes equations describe the balance of forces acting at any given region of the fluid.
The Navier–Stokes equations are differential equations which describe the motion of a fluid. Such equations establish relations among the rates of change of the variables of interest. For example, the Navier–Stokes equations for an ideal fluid with zero viscosity states that acceleration (the rate of change of velocity) is proportional to the derivative of internal pressure.
This means that solutions of the Navier–Stokes equations for a given physical problem must be sought with the help of calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
. In practical terms only the simplest cases can be solved exactly in this way. These cases generally involve non-turbulent, steady flow (flow does not change with time) in which the Reynolds number is small.
For more complex situations, such as global weather systems like El Niño or lift in a wing, solutions of the Navier–Stokes equations can currently only be found with the help of computers. This is a field of sciences by its own called computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
.
General form of the equation
The general form of the Navier–Stokes equations for the conservation of momentum is:
where
 is the fluid density,
is the fluid density,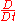 is the substantive derivative (also called the material derivative),
is the substantive derivative (also called the material derivative), is the velocity vector,
is the velocity vector, is the body force vector, and
is the body force vector, and is a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
is a tensorTensorTensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
that represents the surface forces applied on a fluid particle (the stress tensorStress tensorStress tensor may refer to:* Stress , in classical physics* Stress-energy tensor, in relativistic theories* Maxwell stress tensor, in electromagnetism...
).
Unless the fluid is made up of spinning degrees of freedom like vortices,
 is a symmetric tensor. In general, (in three dimensions)
is a symmetric tensor. In general, (in three dimensions)  has the form:
has the form:
where
 are normal stresses,
are normal stresses, are tangential stresses (shear stresses).
are tangential stresses (shear stresses).
The above is actually a set of three equations, one per dimension. By themselves, these aren't sufficient to produce a solution. However, adding conservation of mass and appropriate boundary conditions to the system of equations produces a solvable set of equations.
Newtonian versus non-Newtonian fluids
A Newtonian fluid (named after Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
) is defined to be a fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
whose shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
is linearly proportional to the velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
in the direction perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
to the plane of shear. This definition means regardless of the forces acting on a fluid, it continues to flow. For example, water is a Newtonian fluid, because it continues to display fluid properties no matter how much it is stirred or mixed. A slightly less rigorous definition is that the drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
of a small object being moved slowly through the fluid is proportional to the force applied to the object. (Compare friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
). Important fluids, like water as well as most gases, behave — to good approximation — as a Newtonian fluid under normal conditions on Earth.
By contrast, stirring a non-Newtonian fluid
Non-Newtonian fluid
A non-Newtonian fluid is a fluid whose flow properties differ in any way from those of Newtonian fluids. Most commonly the viscosity of non-Newtonian fluids is not independent of shear rate or shear rate history...
can leave a "hole" behind. This will gradually fill up over time – this behaviour is seen in materials such as pudding, oobleck, or sand
Sand
Sand is a naturally occurring granular material composed of finely divided rock and mineral particles.The composition of sand is highly variable, depending on the local rock sources and conditions, but the most common constituent of sand in inland continental settings and non-tropical coastal...
(although sand isn't strictly a fluid). Alternatively, stirring a non-Newtonian fluid can cause the viscosity to decrease, so the fluid appears "thinner" (this is seen in non-drip paint
Paint
Paint is any liquid, liquefiable, or mastic composition which after application to a substrate in a thin layer is converted to an opaque solid film. One may also consider the digital mimicry thereof...
s). There are many types of non-Newtonian fluids, as they are defined to be something that fails to obey a particular property — for example, most fluids with long molecular chains can react in a non-Newtonian manner.
Equations for a Newtonian fluid
The constant of proportionality between the shear stress and the velocity gradient is known as the viscosityViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. A simple equation to describe Newtonian fluid behaviour is

where
 is the shear stress exerted by the fluid ("drag
is the shear stress exerted by the fluid ("dragDrag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
")
 is the fluid viscosity – a constant of proportionality
is the fluid viscosity – a constant of proportionality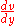 is the velocity gradient perpendicular to the direction of shear.
is the velocity gradient perpendicular to the direction of shear.For a Newtonian fluid, the viscosity, by definition, depends only on temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, not on the forces acting upon it. If the fluid is incompressible and viscosity is constant across the fluid, the equation governing the shear stress (in Cartesian coordinates
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
) is
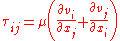
where
 is the shear stress on the
is the shear stress on the  face of a fluid element in the
face of a fluid element in the 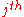 direction
direction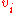 is the velocity in the
is the velocity in the  direction
direction is the
is the  direction coordinate.
direction coordinate.If a fluid does not obey this relation, it is termed a non-Newtonian fluid
Non-Newtonian fluid
A non-Newtonian fluid is a fluid whose flow properties differ in any way from those of Newtonian fluids. Most commonly the viscosity of non-Newtonian fluids is not independent of shear rate or shear rate history...
, of which there are several types.
Among fluids, two rough broad divisions can be made: ideal and non-ideal fluids. An ideal fluid really does not exist, but in some calculations, the assumption is justifiable. An Ideal fluid is non viscous- offers no resistance whatsoever to a shearing force.
One can group real fluids into Newtonian and non-Newtonian. Newtonian fluids agree with Newton's law of viscosity. Non-Newtonian fluids can be either plastic, bingham plastic, pseudoplastic, dilatant, thixotropic, rheopectic, viscoelatic.
See also
- AerodynamicsAerodynamicsAerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
- Applied mechanicsApplied mechanicsApplied mechanics is a branch of the physical sciences and the practical application of mechanics. Applied mechanics examines the response of bodies or systems of bodies to external forces...
- Secondary flowSecondary flowIn fluid dynamics, a secondary flow is a relatively minor flow superimposed on the primary flow, where the primary flow usually matches very closely the flow pattern predicted using simple analytical techniques and assuming the fluid is inviscid...
- Bernoulli's principleBernoulli's principleIn fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
- Communicating vesselsCommunicating vesselsCommunicating vessels is a name given to a set of containers containing a homogeneous fluid: when the liquid settles, it balances out to the same level in all of the containers regardless of the shape and volume of the containers...
External links
- Free Fluid Mechanics books
- Fluid Mechanics webpage by Falkovich
- Annual Review of Fluid Mechanics
- CFDWiki – the Computational Fluid Dynamics reference wiki.
- Educational Particle Image Velocimetry – resources and demonstrations
- prof. DSc Ivan Antonov, Technical University of Sofia, Bulgaria.

