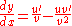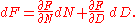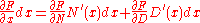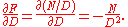Quotient rule
Encyclopedia
In calculus
, the quotient rule is a method of finding the derivative
of a function
that is the quotient
of two other functions for which derivatives exist.
If the function one wishes to differentiate,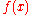 , can be written as
, can be written as

and , then the rule states that the derivative of
, then the rule states that the derivative of 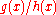 is
is

More precisely, if all x in some open set
containing the number a satisfy , and
, and  and
and 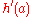 both exist, then
both exist, then 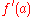 exists as well and
exists as well and
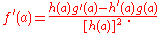
And this can be extended to calculate the second derivative as well (you can prove this by taking the derivative of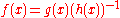 twice). The result of this is:
twice). The result of this is:
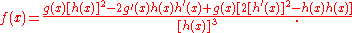
The quotient rule formula can be derived from the product rule
and chain rule
.
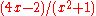 is:
is:

In the example above, the choices


were made. Analogously, the derivative of sin(x)/x2 (when x ≠ 0) is:
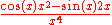
Another example is:

whereas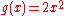 and
and 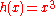 , and
, and  and
and 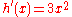 .
.
The derivative of is determined as follows:
is determined as follows:
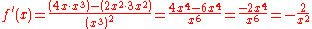
This can be checked by using laws of exponents and the power rule:

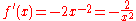
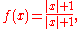
where |x| denotes the absolute value
of x. This is, of course, simply the function f(x) = 1, so it is differentiable everywhere and in particular f'(0) = 0. If we try to use the quotient rule to compute f'(0), however, an undefined value will result, since |x| is nondifferentiable at x = 0.
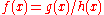 where
where  and
and  and
and  are differentiable
are differentiable
.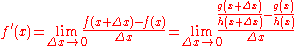
We pull out the and combine the fractions in the numerator:
and combine the fractions in the numerator: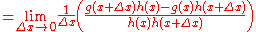
Adding and subtracting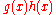 in the numerator:
in the numerator: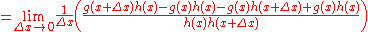
We factor this and multiply the through the numerator:
through the numerator:
Now we move the limit through: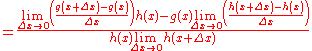
By the definition of the derivative, the limits of difference quotient
s in the numerator are derivative
s. The limit in the denominator is h(x) because differentiable functions are continuous. Thus we get:
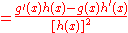

Then
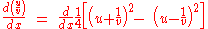
Leading to
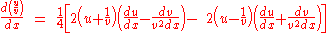
Multiplying out leads to

Finally, taking a common denominator leaves us with the expected result
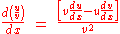

Rewriting in indices form
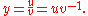
Using the product rule and the chain rule to differentiate leads us to,
Cross multiplying and through simple algebraic manipulation we get,
Which is the quotient rule.
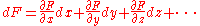
of any function in any set of quantities is decomposable in this way, no matter what the independent variable
s in a function are (i.e., no matter which variables are taken so that they may not be expressed as functions of other variables). This means that, if N and D are both functions of an independent variable x, and F = N(x)/D(x), then it must be true both that
and that
But we know that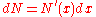 and
and 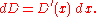
Substituting and setting these two total differentials equal to one another (since they represent limits which we can manipulate), we obtain the equation
which requires that
We compute the partials on the right:
If we substitute them into (#),
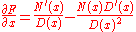
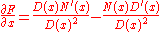
which gives us the quotient rule, since, by (*),
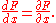
This proof, of course, is just another, more systematic (even if outmoded) way of proving the theorem in terms of limits, and is therefore equivalent to the first proof above – and even reduces to it, if you make the right substitutions in the right places. Students of multivariable calculus will recognize it as one of the chain rules for functions of multiple variables.
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, the quotient rule is a method of finding the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that is the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
of two other functions for which derivatives exist.
If the function one wishes to differentiate,
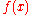 , can be written as
, can be written as
and
 , then the rule states that the derivative of
, then the rule states that the derivative of 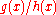 is
is
More precisely, if all x in some open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
containing the number a satisfy
 , and
, and  and
and 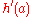 both exist, then
both exist, then 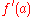 exists as well and
exists as well and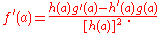
And this can be extended to calculate the second derivative as well (you can prove this by taking the derivative of
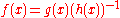 twice). The result of this is:
twice). The result of this is: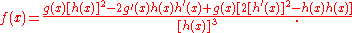
The quotient rule formula can be derived from the product rule
Product rule
In calculus, the product rule is a formula used to find the derivatives of products of two or more functions. It may be stated thus:'=f'\cdot g+f\cdot g' \,\! or in the Leibniz notation thus:...
and chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
.
Examples
The derivative of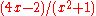 is:
is:
In the example above, the choices


were made. Analogously, the derivative of sin(x)/x2 (when x ≠ 0) is:
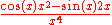
Another example is:

whereas
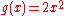 and
and 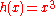 , and
, and  and
and 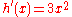 .
.The derivative of
 is determined as follows:
is determined as follows: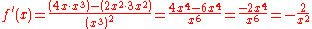
This can be checked by using laws of exponents and the power rule:

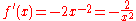
Limitations
The quotient rule is not useful at points where either the numerator or denominator are not differentiable; it's possible that the quotient may be differentiable at such points. For example, consider the function: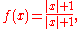
where |x| denotes the absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
of x. This is, of course, simply the function f(x) = 1, so it is differentiable everywhere and in particular f'(0) = 0. If we try to use the quotient rule to compute f'(0), however, an undefined value will result, since |x| is nondifferentiable at x = 0.
Algebraic proof
Link to external websiteFrom Newton's difference quotient
Suppose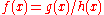 where
where  and
and  and
and  are differentiable
are differentiableDerivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
.
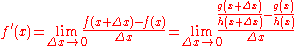
We pull out the
 and combine the fractions in the numerator:
and combine the fractions in the numerator: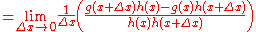
Adding and subtracting
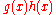 in the numerator:
in the numerator: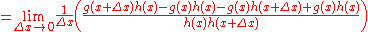
We factor this and multiply the
 through the numerator:
through the numerator:
Now we move the limit through:
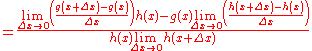
By the definition of the derivative, the limits of difference quotient
Difference quotient
The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...
s in the numerator are derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s. The limit in the denominator is h(x) because differentiable functions are continuous. Thus we get:
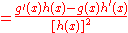
Using the chain rule
Consider the identity
Then
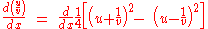
Leading to
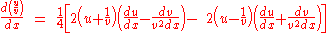
Multiplying out leads to

Finally, taking a common denominator leaves us with the expected result
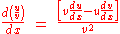
Using the product rule
Let
Rewriting in indices form
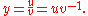
Using the product rule and the chain rule to differentiate leads us to,
Cross multiplying and through simple algebraic manipulation we get,
Which is the quotient rule.
By total differentials
An even more elegant proof is a consequence of the law about total differentials, which states that the total differential,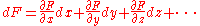
of any function in any set of quantities is decomposable in this way, no matter what the independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
s in a function are (i.e., no matter which variables are taken so that they may not be expressed as functions of other variables). This means that, if N and D are both functions of an independent variable x, and F = N(x)/D(x), then it must be true both that
and that
But we know that
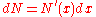 and
and 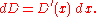
Substituting and setting these two total differentials equal to one another (since they represent limits which we can manipulate), we obtain the equation
which requires that
We compute the partials on the right:
If we substitute them into (#),
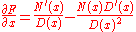
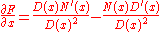
which gives us the quotient rule, since, by (*),
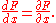
This proof, of course, is just another, more systematic (even if outmoded) way of proving the theorem in terms of limits, and is therefore equivalent to the first proof above – and even reduces to it, if you make the right substitutions in the right places. Students of multivariable calculus will recognize it as one of the chain rules for functions of multiple variables.