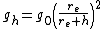Earth's gravity
Encyclopedia
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
that the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
imparts to objects on or near its surface
Elevation
The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....
. In SI units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
this acceleration is measured in metres per second per second (in symbols, m
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
/s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
2 or m
Metre
The metre , symbol m, is the base unit of length in the International System of Units . Originally intended to be one ten-millionth of the distance from the Earth's equator to the North Pole , its definition has been periodically refined to reflect growing knowledge of metrology...
·s
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
-2) or equivalently in newtons per kilogram (N/kg
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
or N·kg
Kilogram
The kilogram or kilogramme , also known as the kilo, is the base unit of mass in the International System of Units and is defined as being equal to the mass of the International Prototype Kilogram , which is almost exactly equal to the mass of one liter of water...
-1). It has an approximate value of 9.81 m/s2, which means that, ignoring the effects of air resistance, the speed
Speed
In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
of an object falling freely
Free fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
near the Earth's surface will increase by about 9.81 metres (about 32 ft) per second every second. This quantity is sometimes referred to informally as little g (in contrast, the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G is referred to as big G).
There is a direct relationship between gravitational acceleration
Gravitational acceleration
In physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
and the downwards weight
Weight
In science and engineering, the weight of an object is the force on the object due to gravity. Its magnitude , often denoted by an italic letter W, is the product of the mass m of the object and the magnitude of the local gravitational acceleration g; thus:...
force experienced by objects on Earth, given by the equation F = ma
Newton's laws of motion
Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...
(force = mass × acceleration). However, other factors such as the rotation of the Earth also contribute to the net acceleration.
Although the precise strength of Earth's gravity varies depending on location, the nominal "average" value at the Earth's surface, known as is, by definition, 9.80665 m/s2 (32.1740 ft/s2). This quantity is denoted variously as gn, ge (though this sometimes means the normal equatorial value on Earth, 9.78033 m/s2), g0, gee, or simply g (which is also used for the variable local value). The symbol g should not be confused with g, the abbreviation for gram (which is not italicized).
Variation in gravity and apparent gravity
A perfect sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of spherically uniform density
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
(density varies solely with distance from centre) would produce a gravitational field of uniform magnitude at all points on its surface
Surface
In mathematics, specifically in topology, a surface is a two-dimensional topological manifold. The most familiar examples are those that arise as the boundaries of solid objects in ordinary three-dimensional Euclidean space R3 — for example, the surface of a ball...
, always pointing directly towards the sphere's centre. However, the Earth deviates slightly from this ideal, and there are consequently slight deviations in both the magnitude and direction of gravity across its surface. Furthermore, the net force
Net force
In physics, net force is the total force acting on an object. It is calculated by vector addition of all forces that are actually acting on that object. Net force has the same effect on the translational motion of the object as all actual forces taken together...
exerted on an object due to the Earth, called "effective gravity" or "apparent gravity", varies due to the presence of other forces, such as the centrifugal force of Earth's rotation. A scale or plumb bob measures only this effective gravity.
Parameters affecting the apparent or actual strength of Earth's gravity include latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
, altitude
Altitude
Altitude or height is defined based on the context in which it is used . As a general definition, altitude is a distance measurement, usually in the vertical or "up" direction, between a reference datum and a point or object. The reference datum also often varies according to the context...
, and the local topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
and geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
.
Latitude
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
produced by Earth's rotation is stronger than at polar latitudes. This counteracts the Earth's gravity to a small degree – up to a maximum of 0.3% at the Equator – reducing the downward acceleration of falling objects.
The second major cause for the difference in gravity at different latitudes is that the Earth's equatorial bulge
Equatorial bulge
An equatorial bulge is a difference between the equatorial and polar diameters of a planet, due to the centrifugal force of its rotation. A rotating body tends to form an oblate spheroid rather than a sphere...
(itself also caused by centrifugal force) causes objects at the Equator to be farther from the planet's centre than objects at the poles. Because the force due to gravitational attraction between two bodies (the Earth and the object being weighed) varies inversely with the square of the distance between them, an object at the Equator experiences a weaker gravitational pull than an object at the poles.
In combination, the equatorial bulge and the effects of centrifugal force mean that sea-level gravitational acceleration increases from about 9.780 m·s−2 at the Equator to about 9.832 m·s−2 at the poles, so an object will weigh about 0.5% more at the poles than at the Equator.
The same two factors influence the direction of the effective gravity. Anywhere on Earth away from the Equator or poles, effective gravity points not exactly toward the centre of the Earth, but rather perpendicular to the surface of the geoid
Geoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
, which, due to the flattened shape of the Earth, is somewhat toward the opposite pole. About half of the deflection is due to centrifugal force, and half because the extra mass around the Equator causes a change in the direction of the true gravitational force relative to what it would be on a spherical Earth.
Altitude
Mount Everest
Mount Everest is the world's highest mountain, with a peak at above sea level. It is located in the Mahalangur section of the Himalayas. The international boundary runs across the precise summit point...
(8,850 metres) causes a weight decrease of about 0.28%. (An additional factor affecting apparent weight is the decrease in air density at altitude, which lessens an object's buoyancy.) It is a common misconception that astronauts in orbit are weightless because they have flown high enough to "escape" the Earth's gravity. In fact, at an altitude of 400 kilometres (250 miles), equivalent to a typical orbit of the Space Shuttle
Space Shuttle
The Space Shuttle was a manned orbital rocket and spacecraft system operated by NASA on 135 missions from 1981 to 2011. The system combined rocket launch, orbital spacecraft, and re-entry spaceplane with modular add-ons...
, gravity is still nearly 90% as strong as at the Earth's surface, and weightlessness actually occurs because orbiting objects are in free-fall
Free-fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
.
The following formula approximates the Earth's gravity variation with altitude:
Where
-
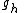 is the gravitational acceleration at height
is the gravitational acceleration at height 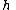 above sea level.
above sea level. -
 is the Earth's mean radiusEarth radiusBecause the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
is the Earth's mean radiusEarth radiusBecause the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
. -
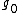 is the standard gravitational acceleration.
is the standard gravitational acceleration.
This formula treats the Earth as a perfect sphere with a radially symmetric distribution of mass; a more accurate mathematical treatment is discussed below.
Depth
If the Earth were a sphere of uniform density then gravity would decrease linearly to zero as one travelled in a straight line from the Earth's surface to its centre. This is a consequence of Gauss' law for gravityGauss' law for gravity
In physics, Gauss's law for gravity, also known as Gauss's flux theorem for gravity, is a law of physics which is essentially equivalent to Newton's law of universal gravitation...
. Because of the spherical symmetry, gravity is radially downward and equal in magnitude at all points at a given radius r. The surface area of a sphere of radius r being 4πr2, Gauss's law gives
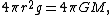
where G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
and M is the total mass enclosed within the surface. Since, for r less than the Earth's radius and a constant density ρ, M = ρ(4/3)πr3, the dependence of gravity on depth is
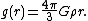
If the density decreases linearly with depth from a density ρ0 at the center to ρ1 at the surface, then ρ(r) = ρ0 - (ρ0-ρ1)r / re, and

The actual depth-dependence of density and gravity, inferred from seismic travel times (see Adams–Williamson equation
Adams–Williamson equation
The Adams–Williamson equation, named after L. H. Adams and E. D. Williamson, is a relation between the velocities of seismic waves and the density of the Earth's interior. Given the average density of rocks at the Earth's surface and profiles of the P-wave and S-wave speeds as function of depth,...
), is shown in the graphs below.
Local topography and geology
- See also physical geodesyPhysical geodesyPhysical geodesy is the study of the physical properties of the gravity field of the Earth, the geopotential, with a view to their application in geodesy.-Measurement procedure:...
.
Local variations in topography
Topography
Topography is the study of Earth's surface shape and features or those ofplanets, moons, and asteroids...
(such as the presence of mountains) and geology
Geology
Geology is the science comprising the study of solid Earth, the rocks of which it is composed, and the processes by which it evolves. Geology gives insight into the history of the Earth, as it provides the primary evidence for plate tectonics, the evolutionary history of life, and past climates...
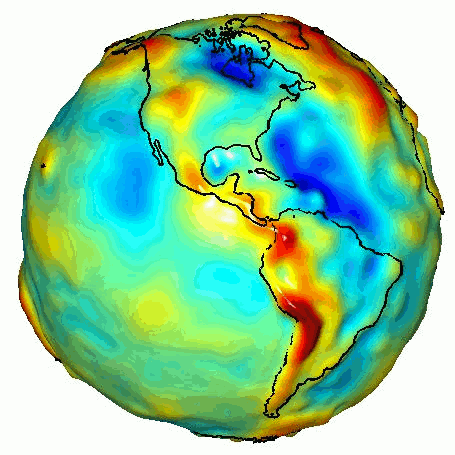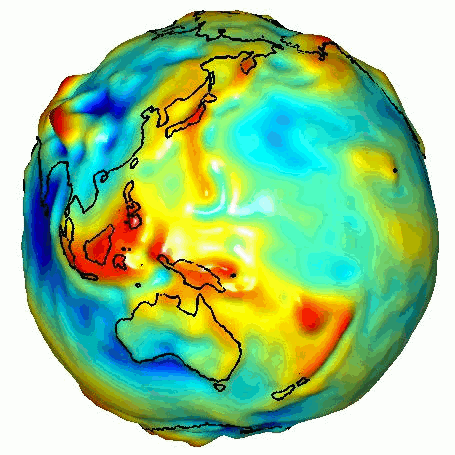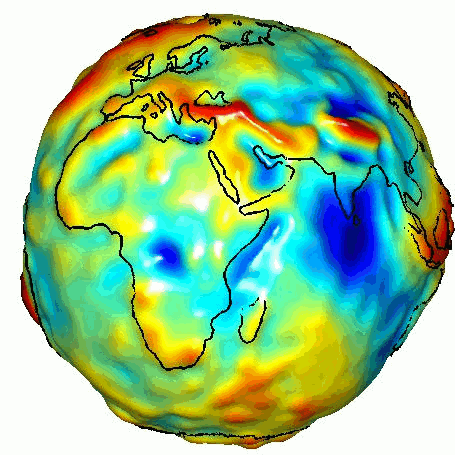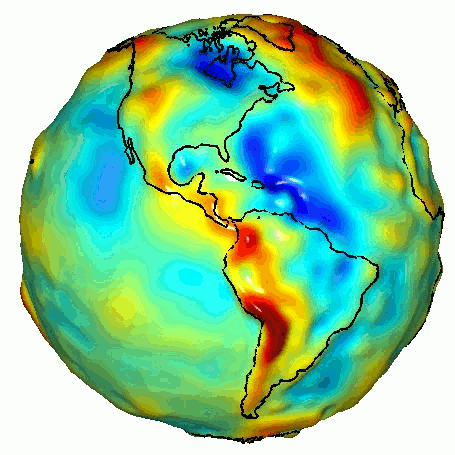
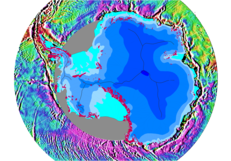
(such as the density of rocks in the vicinity) cause fluctuations in the Earth's gravitational field, known as gravitational anomalies
Gravity anomaly
A gravity anomaly is the difference between the observed acceleration of Earth's gravity and a value predicted from a model.-Geodesy and geophysics:...
. Some of these anomalies can be very extensive, resulting in bulges in sea level
Sea level
Mean sea level is a measure of the average height of the ocean's surface ; used as a standard in reckoning land elevation...
, and throwing pendulum
Pendulum
A pendulum is a weight suspended from a pivot so that it can swing freely. When a pendulum is displaced from its resting equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back toward the equilibrium position...
clocks out of synchronisation.
The study of these anomalies forms the basis of gravitational geophysics
Geophysics
Geophysics is the physics of the Earth and its environment in space; also the study of the Earth using quantitative physical methods. The term geophysics sometimes refers only to the geological applications: Earth's shape; its gravitational and magnetic fields; its internal structure and...
. The fluctuations are measured with highly sensitive gravimeter
Gravimeter
A gravimeter or gravitometer is an instrument used in gravimetry for measuring the local gravitational field of the Earth. A gravimeter is a type of accelerometer, specialized for measuring the constant downward acceleration of gravity, which varies by about 0.5% over the surface of the Earth...
s, the effect of topography and other known factors is subtracted, and from the resulting data conclusions are drawn. Such techniques are now used by prospectors to find oil
Oil
An oil is any substance that is liquid at ambient temperatures and does not mix with water but may mix with other oils and organic solvents. This general definition includes vegetable oils, volatile essential oils, petrochemical oils, and synthetic oils....
and mineral deposits. Denser rocks (often containing mineral ore
Ore
An ore is a type of rock that contains minerals with important elements including metals. The ores are extracted through mining; these are then refined to extract the valuable element....
s) cause higher than normal local gravitational fields on the Earth's surface. Less dense sedimentary rock
Sedimentary rock
Sedimentary rock are types of rock that are formed by the deposition of material at the Earth's surface and within bodies of water. Sedimentation is the collective name for processes that cause mineral and/or organic particles to settle and accumulate or minerals to precipitate from a solution....
s cause the opposite.
Other factors
In air, objects experience a supporting buoyancyBuoyancy
In physics, buoyancy is a force exerted by a fluid that opposes an object's weight. In a column of fluid, pressure increases with depth as a result of the weight of the overlying fluid. Thus a column of fluid, or an object submerged in the fluid, experiences greater pressure at the bottom of the...
force which reduces the apparent strength of gravity (as measured by an object's weight). The magnitude of the effect depends on air density (and hence air pressure); see Apparent weight
Apparent weight
The weight in a given frame of reference is a generalized concept of weight, see the ISO definition of weight.An object's regular weight is its weight with respect to Earth...
for details.
The gravitational effects of the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
and the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
(also the cause of the tide
Tide
Tides are the rise and fall of sea levels caused by the combined effects of the gravitational forces exerted by the moon and the sun and the rotation of the Earth....
s) have a very small effect on the apparent strength of Earth's gravity, depending on their relative positions; typical variations are 2 µm/s² (0.2 mGal
Gal (unit)
The gal, sometimes called galileo, is a unit of acceleration used extensively in the science of gravimetry. The gal is defined as 1 centimeter per second squared ....
) over the course of a day.
Comparative gravities in various cities around the world
The table below shows the gravitational acceleration in various cities around the world; amongst these cities, it is lowest in Mexico City (9.779 m/s²) and highest in Oslo (Norway) and Helsinki (Finland) (9.819 m/s²).| Location | Acceleration in m⁄s² |
|---|---|
| Amsterdam Amsterdam Amsterdam is the largest city and the capital of the Netherlands. The current position of Amsterdam as capital city of the Kingdom of the Netherlands is governed by the constitution of August 24, 1815 and its successors. Amsterdam has a population of 783,364 within city limits, an urban population... |
9.813 |
| Athens Athens Athens , is the capital and largest city of Greece. Athens dominates the Attica region and is one of the world's oldest cities, as its recorded history spans around 3,400 years. Classical Athens was a powerful city-state... |
9.800 |
| Auckland Auckland The Auckland metropolitan area , in the North Island of New Zealand, is the largest and most populous urban area in the country with residents, percent of the country's population. Auckland also has the largest Polynesian population of any city in the world... |
9.799 |
| Bangkok Bangkok Bangkok is the capital and largest urban area city in Thailand. It is known in Thai as Krung Thep Maha Nakhon or simply Krung Thep , meaning "city of angels." The full name of Bangkok is Krung Thep Mahanakhon Amon Rattanakosin Mahintharayutthaya Mahadilok Phop Noppharat Ratchathani Burirom... |
9.783 |
| Brussels Brussels Brussels , officially the Brussels Region or Brussels-Capital Region , is the capital of Belgium and the de facto capital of the European Union... |
9.811 |
| Buenos Aires Buenos Aires Buenos Aires is the capital and largest city of Argentina, and the second-largest metropolitan area in South America, after São Paulo. It is located on the western shore of the estuary of the Río de la Plata, on the southeastern coast of the South American continent... |
9.797 |
| Calcutta | 9.788 |
| Cape Town Cape Town Cape Town is the second-most populous city in South Africa, and the provincial capital and primate city of the Western Cape. As the seat of the National Parliament, it is also the legislative capital of the country. It forms part of the City of Cape Town metropolitan municipality... |
9.796 |
| Chicago Chicago Chicago is the largest city in the US state of Illinois. With nearly 2.7 million residents, it is the most populous city in the Midwestern United States and the third most populous in the US, after New York City and Los Angeles... |
9.803 |
| Copenhagen Copenhagen Copenhagen is the capital and largest city of Denmark, with an urban population of 1,199,224 and a metropolitan population of 1,930,260 . With the completion of the transnational Øresund Bridge in 2000, Copenhagen has become the centre of the increasingly integrating Øresund Region... |
9.815 |
| Frankfurt Frankfurt Frankfurt am Main , commonly known simply as Frankfurt, is the largest city in the German state of Hesse and the fifth-largest city in Germany, with a 2010 population of 688,249. The urban area had an estimated population of 2,300,000 in 2010... |
9.810 |
| Havana Havana Havana is the capital city, province, major port, and leading commercial centre of Cuba. The city proper has a population of 2.1 million inhabitants, and it spans a total of — making it the largest city in the Caribbean region, and the most populous... |
9.788 |
| Helsinki Helsinki Helsinki is the capital and largest city in Finland. It is in the region of Uusimaa, located in southern Finland, on the shore of the Gulf of Finland, an arm of the Baltic Sea. The population of the city of Helsinki is , making it by far the most populous municipality in Finland. Helsinki is... |
9.819 |
| Istanbul Istanbul Istanbul , historically known as Byzantium and Constantinople , is the largest city of Turkey. Istanbul metropolitan province had 13.26 million people living in it as of December, 2010, which is 18% of Turkey's population and the 3rd largest metropolitan area in Europe after London and... |
9.808 |
| Jakarta Jakarta Jakarta is the capital and largest city of Indonesia. Officially known as the Special Capital Territory of Jakarta, it is located on the northwest coast of Java, has an area of , and a population of 9,580,000. Jakarta is the country's economic, cultural and political centre... |
9.781 |
| Kuwait Kuwait The State of Kuwait is a sovereign Arab state situated in the north-east of the Arabian Peninsula in Western Asia. It is bordered by Saudi Arabia to the south at Khafji, and Iraq to the north at Basra. It lies on the north-western shore of the Persian Gulf. The name Kuwait is derived from the... |
9.793 |
| Lisbon Lisbon Lisbon is the capital city and largest city of Portugal with a population of 545,245 within its administrative limits on a land area of . The urban area of Lisbon extends beyond the administrative city limits with a population of 3 million on an area of , making it the 9th most populous urban... |
9.801 |
| London London London is the capital city of :England and the :United Kingdom, the largest metropolitan area in the United Kingdom, and the largest urban zone in the European Union by most measures. Located on the River Thames, London has been a major settlement for two millennia, its history going back to its... |
9.812 |
| Los Angeles Los Ángeles Los Ángeles is the capital of the province of Biobío, in the commune of the same name, in Region VIII , in the center-south of Chile. It is located between the Laja and Biobío rivers. The population is 123,445 inhabitants... |
9.796 |
| Madrid Madrid Madrid is the capital and largest city of Spain. The population of the city is roughly 3.3 million and the entire population of the Madrid metropolitan area is calculated to be 6.271 million. It is the third largest city in the European Union, after London and Berlin, and its metropolitan... |
9.800 |
| Manila Manila Manila is the capital of the Philippines. It is one of the sixteen cities forming Metro Manila.Manila is located on the eastern shores of Manila Bay and is bordered by Navotas and Caloocan to the north, Quezon City to the northeast, San Juan and Mandaluyong to the east, Makati on the southeast,... |
9.784 |
| Mexico City Mexico City Mexico City is the Federal District , capital of Mexico and seat of the federal powers of the Mexican Union. It is a federal entity within Mexico which is not part of any one of the 31 Mexican states but belongs to the federation as a whole... |
9.779 |
| Montréal Montreal Montreal is a city in Canada. It is the largest city in the province of Quebec, the second-largest city in Canada and the seventh largest in North America... |
9.789 |
| New York City New York City New York is the most populous city in the United States and the center of the New York Metropolitan Area, one of the most populous metropolitan areas in the world. New York exerts a significant impact upon global commerce, finance, media, art, fashion, research, technology, education, and... |
9.802 |
| Nicosia Nicosia Nicosia from , known locally as Lefkosia , is the capital and largest city in Cyprus, as well as its main business center. Nicosia is the only divided capital in the world, with the southern and the northern portions divided by a Green Line... |
9.797 |
| Oslo Oslo Oslo is a municipality, as well as the capital and most populous city in Norway. As a municipality , it was established on 1 January 1838. Founded around 1048 by King Harald III of Norway, the city was largely destroyed by fire in 1624. The city was moved under the reign of Denmark–Norway's King... |
9.819 |
| Ottawa Ottawa Ottawa is the capital of Canada, the second largest city in the Province of Ontario, and the fourth largest city in the country. The city is located on the south bank of the Ottawa River in the eastern portion of Southern Ontario... |
9.806 |
| Paris Paris Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region... |
9.809 |
| Rio de Janeiro Rio de Janeiro Rio de Janeiro , commonly referred to simply as Rio, is the capital city of the State of Rio de Janeiro, the second largest city of Brazil, and the third largest metropolitan area and agglomeration in South America, boasting approximately 6.3 million people within the city proper, making it the 6th... |
9.788 |
| Rome Rome Rome is the capital of Italy and the country's largest and most populated city and comune, with over 2.7 million residents in . The city is located in the central-western portion of the Italian Peninsula, on the Tiber River within the Lazio region of Italy.Rome's history spans two and a half... |
9.803 |
| San Francisco | 9.800 |
| Singapore Singapore Singapore , officially the Republic of Singapore, is a Southeast Asian city-state off the southern tip of the Malay Peninsula, north of the equator. An island country made up of 63 islands, it is separated from Malaysia by the Straits of Johor to its north and from Indonesia's Riau Islands by the... |
9.781 |
| Stockholm Stockholm Stockholm is the capital and the largest city of Sweden and constitutes the most populated urban area in Scandinavia. Stockholm is the most populous city in Sweden, with a population of 851,155 in the municipality , 1.37 million in the urban area , and around 2.1 million in the metropolitan area... |
9.818 |
| Sydney Sydney Sydney is the most populous city in Australia and the state capital of New South Wales. Sydney is located on Australia's south-east coast of the Tasman Sea. As of June 2010, the greater metropolitan area had an approximate population of 4.6 million people... |
9.797 |
| Taipei Taipei Taipei City is the capital of the Republic of China and the central city of the largest metropolitan area of Taiwan. Situated at the northern tip of the island, Taipei is located on the Tamsui River, and is about 25 km southwest of Keelung, its port on the Pacific Ocean... |
9.790 |
| Tokyo Tokyo , ; officially , is one of the 47 prefectures of Japan. Tokyo is the capital of Japan, the center of the Greater Tokyo Area, and the largest metropolitan area of Japan. It is the seat of the Japanese government and the Imperial Palace, and the home of the Japanese Imperial Family... |
9.798 |
| Vancouver Vancouver Vancouver is a coastal seaport city on the mainland of British Columbia, Canada. It is the hub of Greater Vancouver, which, with over 2.3 million residents, is the third most populous metropolitan area in the country,... |
9.809 |
| Washington, D.C. Washington, D.C. Washington, D.C., formally the District of Columbia and commonly referred to as Washington, "the District", or simply D.C., is the capital of the United States. On July 16, 1790, the United States Congress approved the creation of a permanent national capital as permitted by the U.S. Constitution.... |
9.801 |
| Wellington Wellington Wellington is the capital city and third most populous urban area of New Zealand, although it is likely to have surpassed Christchurch due to the exodus following the Canterbury Earthquake. It is at the southwestern tip of the North Island, between Cook Strait and the Rimutaka Range... |
9.803 |
| Zurich Zürich Zurich is the largest city in Switzerland and the capital of the canton of Zurich. It is located in central Switzerland at the northwestern tip of Lake Zurich... |
9.807 |
Mathematical models
If the terrain is at sea level, we can estimate g: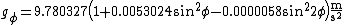
where
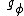 = acceleration in m·s−2 at latitude :
= acceleration in m·s−2 at latitude :
This is the International Gravity Formula 1967, the 1967 Geodetic Reference System Formula, Helmert's equation or Clairaut's formula.
The first correction to this formula is the free air correction (FAC), which accounts for heights above sea level. Gravity decreases with height, at a rate which near the surface of the Earth is such that linear extrapolation would give zero gravity at a height of one half the radius is 9.8 m·s−2 per 3 200 km.
Using the mass and radius of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
:
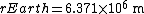
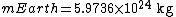
The FAC correction factor (Δg) can be derived from the definition of the acceleration due to gravity in terms of G, the Gravitational Constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
(see Estimating g from the law of universal gravitation, below):
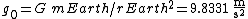
where:
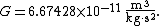
At a height h above the nominal surface of the earth gh is given by:
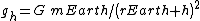
So the FAC for a height h above the nominal earth radius can be expressed:

This expression can be readily used for programming or inclusion in a spreadsheet. Collecting terms, simplifying and neglecting small terms (h<
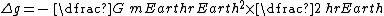
Using the numerical values above and for a height h in metres:
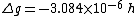
Grouping the latitude and FAC altitude factors the expression most commonly found in the literature is:
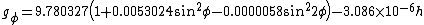
where
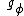 = acceleration in m·s−2 at latitude
= acceleration in m·s−2 at latitude 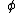 and altitude h in metres. Alternatively (with the same units for h) the expression can be grouped as follows:
and altitude h in metres. Alternatively (with the same units for h) the expression can be grouped as follows: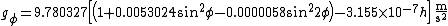
For flat terrain above sea level a second term is added, for the gravity due to the extra mass; for this purpose the extra mass can be approximated by an infinite horizontal slab, and we get 2πG times the mass per unit area, i.e. 4.2 m3·s−2·kg−1 (0.042 μGal·kg−1·m²)) (the Bouguer correction). For a mean rock density of 2.67 g·cm−3 this gives 1.1 s−2 (0.11 mGal·m−1). Combined with the free-air correction this means a reduction of gravity at the surface of ca. 2 µm·s−2 (0.20 mGal) for every metre of elevation of the terrain. (The two effects would cancel at a surface rock density of 4/3 times the average density of the whole Earth.)
For the gravity below the surface we have to apply the free-air correction as well as a double Bouguer correction. With the infinite slab model this is because moving the point of observation below the slab changes the gravity due to it to its opposite. Alternatively, we can consider a spherically symmetrical Earth
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
and subtract from the mass of the Earth that of the shell outside the point of observation, because that does not cause gravity inside. This gives the same result.
Helmert's equation may be written equivalently to the version above as either:
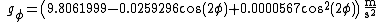
or

An alternate formula for g as a function of latitude is the WGS (World Geodetic System
World Geodetic System
The World Geodetic System is a standard for use in cartography, geodesy, and navigation. It comprises a standard coordinate frame for the Earth, a standard spheroidal reference surface for raw altitude data, and a gravitational equipotential surface that defines the nominal sea level.The latest...
) 84 Ellipsoidal Gravity Formula:
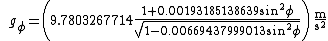
The difference between the WGS-84 formula and Helmert's equation is less than 0.68 · 10−6 m·s−2.
Estimating g from the law of universal gravitation
From the law of universal gravitation, the force on a body acted upon by Earth's gravity is given by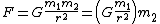
where r is the distance between the centre of the Earth and the body (see below), and here we take m1 to be the mass of the Earth and m2 to be the mass of the body.
Additionally, Newton's second law, F = ma, where m is mass and a is acceleration, here tells us that

Comparing the two formulas it is seen that:
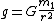
So, to find the acceleration due to gravity at sea level, substitute the values of the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, G, the Earth's mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
(in kilograms), m1, and the Earth's radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
(in metres), r, to obtain the value of g:
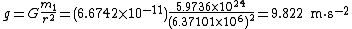
Note that this formula only works because of the mathematical fact that the gravity of a uniform spherical body, as measured on or above its surface, is the same as if all its mass were concentrated at a point at its centre. This is what allows us to use the Earth's radius for r.
The value obtained agrees approximately with the measured value of g. The difference may be attributed to several factors, mentioned above under "Variations":
- The Earth is not homogeneousHomogeneous (chemistry)A substance that is uniform in composition is a definition of homogeneous. This is in contrast to a substance that is heterogeneous.The definition of homogeneous strongly depends on the context used. In Chemistry, a homogeneous suspension of material means that when dividing the volume in half, the...
- The Earth is not a perfect sphere, and an average value must be used for its radius
- This calculated value of g only includes true gravity. It does not include the reduction of constraint force that we perceive as a reduction of gravity due to the rotation of Earth, and some of gravity being "used up" in providing the centripetal acceleration
There are significant uncertainties in the values of r and m1 as used in this calculation, and the value of G
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is also rather difficult to measure precisely.
If G, g and r are known then a reverse calculation will give an estimate of the mass of the Earth. This method was used by Henry Cavendish
Henry Cavendish
Henry Cavendish FRS was a British scientist noted for his discovery of hydrogen or what he called "inflammable air". He described the density of inflammable air, which formed water on combustion, in a 1766 paper "On Factitious Airs". Antoine Lavoisier later reproduced Cavendish's experiment and...
.
Comparative gravities of the Earth, Sun, Moon, and planets
The table below shows comparative gravitational accelerations at the surface of the Sun, the Earth's moon, each of the planets in the solar system and their major moons, Pluto and Eris. The “surface” is taken to mean the cloud tops of the gas giantsGas Giants
Gas Giants were a pop rock band from Tempe, Arizona, formed as a successor project to the Gin Blossoms. The group was known as The Pharaohs when they formed in 1997, but changed their name after their label, A&M Records, merged with Universal Records and the band changed hands, re-signing with...
(Jupiter, Saturn, Uranus and Neptune). For the Sun, the surface is taken to mean the photosphere
Photosphere
The photosphere of an astronomical object is the region from which externally received light originates. The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to the fact that it is a spheric surface perceived...
. The values in the table have not been de-rated for the centrifugal effect of planet rotation (and cloud-top wind speeds for the gas giants) and therefore, generally speaking, are similar to the actual gravity that would be experienced near the poles.
| Body | Multiple of Earth gravity |
m/s2 |
|---|---|---|
| Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
27.90 | 274.1 |
| Mercury Mercury (planet) Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits... |
0.3770 | 3.703 |
| Venus Venus Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows... |
0.9032 | 8.872 |
| Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets... |
1 (by definition) | 9.8067 |
| Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
0.1655 | 1.625 |
| Mars Mars Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance... |
0.3895 | 3.728 |
| Jupiter Jupiter Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,... |
2.640 | 25.93 |
| Io Io (moon) Io ) is the innermost of the four Galilean moons of the planet Jupiter and, with a diameter of , the fourth-largest moon in the Solar System. It was named after the mythological character of Io, a priestess of Hera who became one of the lovers of Zeus.... |
0.182 | 1.789 |
| Europa Europa (moon) Europa Slightly smaller than Earth's Moon, Europa is primarily made of silicate rock and probably has an iron core. It has a tenuous atmosphere composed primarily of oxygen. Its surface is composed of ice and is one of the smoothest in the Solar System. This surface is striated by cracks and... |
0.134 | 1.314 |
| Ganymede Ganymede (moon) Ganymede is a satellite of Jupiter and the largest moon in the Solar System. It is the seventh moon and third Galilean satellite outward from Jupiter. Completing an orbit in roughly seven days, Ganymede participates in a 1:2:4 orbital resonance with the moons Europa and Io, respectively... |
0.145 | 1.426 |
| Callisto Callisto (moon) Callisto named after the Greek mythological figure of Callisto) is a moon of the planet Jupiter. It was discovered in 1610 by Galileo Galilei. It is the third-largest moon in the Solar System and the second largest in the Jovian system, after Ganymede. Callisto has about 99% the diameter of the... |
0.126 | 1.24 |
| Saturn Saturn Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,... |
1.139 | 11.19 |
| Titan Titan (moon) Titan , or Saturn VI, is the largest moon of Saturn, the only natural satellite known to have a dense atmosphere, and the only object other than Earth for which clear evidence of stable bodies of surface liquid has been found.... |
0.138 | 1.3455 |
| Uranus Uranus Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus... |
0.917 | 9.01 |
| Titania Titania (moon) Titania is the largest of the moons of Uranus and the eighth largest moon in the Solar System at a diameter of 1578 km. Discovered by William Herschel in 1787, Titania is named after the queen of the fairies in Shakespeare's A Midsummer Night's Dream... |
0.039 | 0.379 |
| Oberon Oberon (moon) Oberon , also designated ', is the outermost major moon of the planet Uranus. It is the second largest and second most massive of the Uranian moons, and the ninth most massive moon in the Solar System. Discovered by William Herschel in 1787, Oberon is named after the mythical king of the fairies... |
0.035 | 0.347 |
| Neptune Neptune Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times... |
1.148 | 11.28 |
| Triton Triton (moon) Triton is the largest moon of the planet Neptune, discovered on October 10, 1846, by English astronomer William Lassell. It is the only large moon in the Solar System with a retrograde orbit, which is an orbit in the opposite direction to its planet's rotation. At 2,700 km in diameter, it is... |
0.079 | 0.779 |
| Pluto Pluto Pluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun... |
0.0621 | 0.610 |
| Eris Eris (dwarf planet) Eris, formal designation 136199 Eris, is the most massive known dwarf planet in the Solar System and the ninth most massive body known to orbit the Sun directly... |
0.0814 (approx.) | 0.8 (approx.) |
See also
- Earth's magnetic fieldEarth's magnetic fieldEarth's magnetic field is the magnetic field that extends from the Earth's inner core to where it meets the solar wind, a stream of energetic particles emanating from the Sun...
- GravitationGravitationGravitation, or gravity, is a natural phenomenon by which physical bodies attract with a force proportional to their mass. Gravitation is most familiar as the agent that gives weight to objects with mass and causes them to fall to the ground when dropped...
- Gravity anomalyGravity anomalyA gravity anomaly is the difference between the observed acceleration of Earth's gravity and a value predicted from a model.-Geodesy and geophysics:...
, Bouguer correction - Gravitation of the MoonGravitation of the Moonright|thumb|300px|Radial gravity anomaly at the surface of the Moon in [[Gal ]]The gravitational field of the Moon has been determined by the tracking of radio signals emitted by orbiting spacecraft...
- Gravitational accelerationGravitational accelerationIn physics, gravitational acceleration is the acceleration on an object caused by gravity. Neglecting friction such as air resistance, all small bodies accelerate in a gravitational field at the same rate relative to the center of mass....
- Gravity Recovery and Climate ExperimentGravity Recovery and Climate ExperimentThe Gravity Recovery And Climate Experiment , a joint mission of NASA and the German Space Agency, has been making detailed measurements of Earth's gravity field since its launch in March 2002....
- Newton's law of universal gravitationNewton's law of universal gravitationNewton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...