Net force
Encyclopedia
In physics
, net force is the total force
acting on an object. It is calculated by vector addition of all forces that are actually acting on that object. Net force has the same effect on the translational motion of the object as all actual forces taken together. It is always possible to determine the net force (including the case when its amount is zero).
In addition to this, resultant force also has the same effect on the rotational motion of the object as all actual forces taken together. The net force becomes the resultant force when it is assigned the position (i.e. the line of action) that ensures such rotational effect. This is not always possible.
A force acting on an object may cause changes in the motion or in the shape (configuration) of the object. When two or more forces are acting on an object, the concepts of net force and resultant force are intended to simplify description of their effect on its motion.
If the forces are acting on a particle (the size of the object is so small that it can be approximated by a point), they can only change its velocity. In that case, there is no difference between the net force and the resultant force because no rotation is associated with such objects.
If the object is an extended but rigid body (no change in shape), the forces can change its linear velocity as well as its angular velocity. In that case, it may be useful to distinguish the resultant force from the net force. And even in the case of non-rigid objects (deformable bodies or systems), the concepts of net and resultant force are equally applicable to description of their overall motion.
Some authors use "resultant force" and "net force" as synonyms, even when the forces act on extended bodies. However, this is generally not the case (see the note at the end of the article) in mechanics
and in those technical applications where full understanding and actual calculations of the rotating body dynamics (or even of the static equilibrium) are required.
quantity, which means that it has a magnitude and a direction, and it is usually denoted by the symbol . Graphically it is represented by an oriented straight line segment: its direction is the direction of the oriented line, and its magnitude is proportional to length of the line (more precisely, one can specify how many newtons are represented by one centimeter).
. Graphically it is represented by an oriented straight line segment: its direction is the direction of the oriented line, and its magnitude is proportional to length of the line (more precisely, one can specify how many newtons are represented by one centimeter).
Although vector calculus was developing as late as the 18th and 19th century, the parallelogram rule for addition of forces is claimed to date from the Old Greek times, and it is explicitly noted by Galileo and Newton. Diagram shows the addition of the forces and
and  . The sum
. The sum  of the two forces is drawn as the diagonal of the parallelogram (on the left side). This can be grasped intuitively: if the total force
of the two forces is drawn as the diagonal of the parallelogram (on the left side). This can be grasped intuitively: if the total force  should describe the joint effect of the two forces on a particle (which is the intrinsic meaning of addition), its direction should be closer to the direction of the stronger force
should describe the joint effect of the two forces on a particle (which is the intrinsic meaning of addition), its direction should be closer to the direction of the stronger force  , and its amount should be greater than the amount of
, and its amount should be greater than the amount of  because
because  also helps in pulling the particle in that "general" direction (for the forces shown in the diagram).
also helps in pulling the particle in that "general" direction (for the forces shown in the diagram).
Independent of this approximate intuitive judgement, the rule of parallelogram gives the exact result, which is easily verified by measuring the effects of the forces. The result can be approximately evaluated from the diagram or, based on the diagram, precisely calculated using elementary trigonometry.
Instead of using the parallelogram rule, the same result can be obtained by a simpler procedure (shown on the right side of the diagram). The line segments representing the original forces can be translated (in any order) so that one begins where the other ends. The same result for the vector sum is the line drawn from the beginning of the first segment to the end of the second - or to the end of the last one - which enables simple addition of more than two vectors. At the bottom of the diagram, this procedure is applied to the addition of two parallel and antiparallel forces, leading to the intuitively expected result: for parallel forces the amounts add up, whereas for the forces in opposite directions (antiparallel) the amount of the smaller force is subtracted from the bigger one.
The sum of forces actually acting on an object, obtained by the above procedure of vector addition, is a new force that is called the total force or the net force. If the actual forces are acting on the particle, the net force is a single force that can replaces their effect on the particle motion: it gives the particle the same acceleration as all those actual forces together. This acceleration is described by the Newton's second law of motion.
On the other hand, if the forces are acting on an extended body, or a system of objects, the concept of center of mass is introduced in order to enable direct application of the Newton's second law. In that case, the net force gives the same acceleration to the center of mass as do all the actual forces together. This can be stated, more loosely, that net force describes translational effects of actual forces.
However, in order to account for the full effect of forces on the motion of an extended object, its rotation must also be considered.
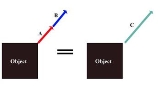
In any case, the analysis of the rigid body motion begins with the point force model. And when a force acting on a body is shown graphically, the oriented line segment representing the force is usually drawn so as to "begin" (or "end") at the application point.
 acts at the application point H on a free rigid body. The body has the mass
acts at the application point H on a free rigid body. The body has the mass  and its center of mass is the point C. In the constant mass approximation, the force causes changes in the body motion described by the following expressions:
and its center of mass is the point C. In the constant mass approximation, the force causes changes in the body motion described by the following expressions:
 is the center of mass acceleration; and
is the center of mass acceleration; and
 is the angular acceleration of the body.
is the angular acceleration of the body.
In the second expression, is the torque
is the torque
or moment of force, whereas is the moment of inertia
is the moment of inertia
of the body. A torque caused by a force is a vector quantity defined with respect to some reference point:
is a vector quantity defined with respect to some reference point:
 is the torque vector, and
is the torque vector, and
 is the amount of torque.
is the amount of torque.
The vector is the position vector of the force application point, and in this example it is drawn from the center of mass as the reference point (see diagram). The straight line segment
is the position vector of the force application point, and in this example it is drawn from the center of mass as the reference point (see diagram). The straight line segment  is the lever arm of the force
is the lever arm of the force  with respect to the center of mass. As the illustration suggests, the torque does not change (the same lever arm) if the application point is moved along the line of the application of the force (dotted black line). More formally, this follows from the properties of the vector product, and shows that rotational effect of the force depends only on the position of its line of application, and not on the particular choice of the point of application along that line.
with respect to the center of mass. As the illustration suggests, the torque does not change (the same lever arm) if the application point is moved along the line of the application of the force (dotted black line). More formally, this follows from the properties of the vector product, and shows that rotational effect of the force depends only on the position of its line of application, and not on the particular choice of the point of application along that line.
The torque vector is perpendicular to the plane defined by the force and the vector , and in this example it is directed towards the observer; the angular acceleration vector has the same direction. The right hand rule relates this direction to the clockwise or counter-clockwise rotation in the plane of the drawing.
, and in this example it is directed towards the observer; the angular acceleration vector has the same direction. The right hand rule relates this direction to the clockwise or counter-clockwise rotation in the plane of the drawing.
The moment of inertia is calculated with respect to the axis through the center of mass that is parallel with the torque. If the body shown in the illustration is a homogenous disc, this moment of inertia is
is calculated with respect to the axis through the center of mass that is parallel with the torque. If the body shown in the illustration is a homogenous disc, this moment of inertia is  . If the disc has the mass 0,5 kg and the radius 0,8 m, the moment of inertia is 0,16 kgm2. If the amount of force is 2 N, and the lever arm 0,6 m, the amount of torque is 1,2 Nm. At the instant shown, the force gives to the disc the angular acceleration α = M/I = 7,5 rad/s2, and to its center of mass it gives the linear acceleration a = F/m = 4 m/s2.
. If the disc has the mass 0,5 kg and the radius 0,8 m, the moment of inertia is 0,16 kgm2. If the amount of force is 2 N, and the lever arm 0,6 m, the amount of torque is 1,2 Nm. At the instant shown, the force gives to the disc the angular acceleration α = M/I = 7,5 rad/s2, and to its center of mass it gives the linear acceleration a = F/m = 4 m/s2.
where is the net force that becomes the resultant force when and if an appropriate position vector
is the net force that becomes the resultant force when and if an appropriate position vector  of its application point can be found; actual individual forces are denoted as
of its application point can be found; actual individual forces are denoted as  and their respective application points by
and their respective application points by  . All torques are calculated with respect to the same arbitrarily selected point.
. All torques are calculated with respect to the same arbitrarily selected point.
The above equation may have no solution for . In that case there is no resultant force, i.e. no single force can replace all actual forces regarding both linear and angular acceleration of the body. And even when
. In that case there is no resultant force, i.e. no single force can replace all actual forces regarding both linear and angular acceleration of the body. And even when  can be calculated, it is not unique, because the point of application can move along the line of application without affecting the torque.
can be calculated, it is not unique, because the point of application can move along the line of application without affecting the torque.
The diagram illustrates simple graphical methods for finding the line of application of the resultant force of simple planar systems.
Most generally, a system of forces acting on a rigid body can always be replaced by one force plus one "pure" torque. The force is the net force, but in order to calculate the additional torque, the net force must be assigned the line of action. The line of action can be selected arbitrarily, but the additional "pure" torque will depend on this choice. In the special case when it is possible to find such line of action that this additional torque is zero, the net force becomes the resultant force.
Some authors do not attribute any significance to this special case, particularly if they do not use it in practical calculations. Therefore, they do not distinguish the resultant force from the net force, i.e. they use the terms as synonyms, or arbitrarily use only one of them to denote the net force.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, net force is the total force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
acting on an object. It is calculated by vector addition of all forces that are actually acting on that object. Net force has the same effect on the translational motion of the object as all actual forces taken together. It is always possible to determine the net force (including the case when its amount is zero).
In addition to this, resultant force also has the same effect on the rotational motion of the object as all actual forces taken together. The net force becomes the resultant force when it is assigned the position (i.e. the line of action) that ensures such rotational effect. This is not always possible.
A force acting on an object may cause changes in the motion or in the shape (configuration) of the object. When two or more forces are acting on an object, the concepts of net force and resultant force are intended to simplify description of their effect on its motion.
If the forces are acting on a particle (the size of the object is so small that it can be approximated by a point), they can only change its velocity. In that case, there is no difference between the net force and the resultant force because no rotation is associated with such objects.
If the object is an extended but rigid body (no change in shape), the forces can change its linear velocity as well as its angular velocity. In that case, it may be useful to distinguish the resultant force from the net force. And even in the case of non-rigid objects (deformable bodies or systems), the concepts of net and resultant force are equally applicable to description of their overall motion.
Some authors use "resultant force" and "net force" as synonyms, even when the forces act on extended bodies. However, this is generally not the case (see the note at the end of the article) in mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
and in those technical applications where full understanding and actual calculations of the rotating body dynamics (or even of the static equilibrium) are required.
Net force
A force is a vectorVector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
quantity, which means that it has a magnitude and a direction, and it is usually denoted by the symbol
 . Graphically it is represented by an oriented straight line segment: its direction is the direction of the oriented line, and its magnitude is proportional to length of the line (more precisely, one can specify how many newtons are represented by one centimeter).
. Graphically it is represented by an oriented straight line segment: its direction is the direction of the oriented line, and its magnitude is proportional to length of the line (more precisely, one can specify how many newtons are represented by one centimeter).Although vector calculus was developing as late as the 18th and 19th century, the parallelogram rule for addition of forces is claimed to date from the Old Greek times, and it is explicitly noted by Galileo and Newton. Diagram shows the addition of the forces
 and
and  . The sum
. The sum  of the two forces is drawn as the diagonal of the parallelogram (on the left side). This can be grasped intuitively: if the total force
of the two forces is drawn as the diagonal of the parallelogram (on the left side). This can be grasped intuitively: if the total force  should describe the joint effect of the two forces on a particle (which is the intrinsic meaning of addition), its direction should be closer to the direction of the stronger force
should describe the joint effect of the two forces on a particle (which is the intrinsic meaning of addition), its direction should be closer to the direction of the stronger force  , and its amount should be greater than the amount of
, and its amount should be greater than the amount of  because
because  also helps in pulling the particle in that "general" direction (for the forces shown in the diagram).
also helps in pulling the particle in that "general" direction (for the forces shown in the diagram).Independent of this approximate intuitive judgement, the rule of parallelogram gives the exact result, which is easily verified by measuring the effects of the forces. The result can be approximately evaluated from the diagram or, based on the diagram, precisely calculated using elementary trigonometry.
Instead of using the parallelogram rule, the same result can be obtained by a simpler procedure (shown on the right side of the diagram). The line segments representing the original forces can be translated (in any order) so that one begins where the other ends. The same result for the vector sum is the line drawn from the beginning of the first segment to the end of the second - or to the end of the last one - which enables simple addition of more than two vectors. At the bottom of the diagram, this procedure is applied to the addition of two parallel and antiparallel forces, leading to the intuitively expected result: for parallel forces the amounts add up, whereas for the forces in opposite directions (antiparallel) the amount of the smaller force is subtracted from the bigger one.
The sum of forces actually acting on an object, obtained by the above procedure of vector addition, is a new force that is called the total force or the net force. If the actual forces are acting on the particle, the net force is a single force that can replaces their effect on the particle motion: it gives the particle the same acceleration as all those actual forces together. This acceleration is described by the Newton's second law of motion.
On the other hand, if the forces are acting on an extended body, or a system of objects, the concept of center of mass is introduced in order to enable direct application of the Newton's second law. In that case, the net force gives the same acceleration to the center of mass as do all the actual forces together. This can be stated, more loosely, that net force describes translational effects of actual forces.
However, in order to account for the full effect of forces on the motion of an extended object, its rotation must also be considered.
Point forces
When a force acts on a particle, it is applied to a single point (the particle volume is negligible): this is a point force and the particle is its application point. But an external force on an extended body (object) can be applied to a number of its constituent particles, i.e. can be "spread" over some volume or surface of the body. However, in order to determine its rotational effect on the body, it is necessary to specify its point of application (actually, the line of application, as explained below). The problem is usually resolved in the following ways:- Often the volume or surface on which the force acts is relatively small compared to the size of the body, so that it can be approximated by a point. It is usually not difficult to determine whether the error caused by such approximation is acceptable.
- If it is not acceptable (obviously e.g. in the case of gravitational force), such "volume/surface" force should be described as a system of forces (components), each acting on a single particle, and then the calculation should be done for each of them separately. Such a calculation is typically simplified by the use of differential elements of the body volume/surface, and the integral calculus. In a number of cases, though, it can be shown that such a system of forces may be replaced by a single point force without the actual calculation (as in the case of uniform gravitational force).
In any case, the analysis of the rigid body motion begins with the point force model. And when a force acting on a body is shown graphically, the oriented line segment representing the force is usually drawn so as to "begin" (or "end") at the application point.
Rigid bodies
In the example shown on the diagram, a single force acts at the application point H on a free rigid body. The body has the mass
acts at the application point H on a free rigid body. The body has the mass  and its center of mass is the point C. In the constant mass approximation, the force causes changes in the body motion described by the following expressions:
and its center of mass is the point C. In the constant mass approximation, the force causes changes in the body motion described by the following expressions: is the center of mass acceleration; and
is the center of mass acceleration; and is the angular acceleration of the body.
is the angular acceleration of the body.In the second expression,
 is the torque
is the torqueTorque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
or moment of force, whereas
 is the moment of inertia
is the moment of inertiaMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
of the body. A torque caused by a force
 is a vector quantity defined with respect to some reference point:
is a vector quantity defined with respect to some reference point: is the torque vector, and
is the torque vector, and is the amount of torque.
is the amount of torque.The vector
 is the position vector of the force application point, and in this example it is drawn from the center of mass as the reference point (see diagram). The straight line segment
is the position vector of the force application point, and in this example it is drawn from the center of mass as the reference point (see diagram). The straight line segment  is the lever arm of the force
is the lever arm of the force  with respect to the center of mass. As the illustration suggests, the torque does not change (the same lever arm) if the application point is moved along the line of the application of the force (dotted black line). More formally, this follows from the properties of the vector product, and shows that rotational effect of the force depends only on the position of its line of application, and not on the particular choice of the point of application along that line.
with respect to the center of mass. As the illustration suggests, the torque does not change (the same lever arm) if the application point is moved along the line of the application of the force (dotted black line). More formally, this follows from the properties of the vector product, and shows that rotational effect of the force depends only on the position of its line of application, and not on the particular choice of the point of application along that line.The torque vector is perpendicular to the plane defined by the force and the vector
 , and in this example it is directed towards the observer; the angular acceleration vector has the same direction. The right hand rule relates this direction to the clockwise or counter-clockwise rotation in the plane of the drawing.
, and in this example it is directed towards the observer; the angular acceleration vector has the same direction. The right hand rule relates this direction to the clockwise or counter-clockwise rotation in the plane of the drawing.The moment of inertia
 is calculated with respect to the axis through the center of mass that is parallel with the torque. If the body shown in the illustration is a homogenous disc, this moment of inertia is
is calculated with respect to the axis through the center of mass that is parallel with the torque. If the body shown in the illustration is a homogenous disc, this moment of inertia is  . If the disc has the mass 0,5 kg and the radius 0,8 m, the moment of inertia is 0,16 kgm2. If the amount of force is 2 N, and the lever arm 0,6 m, the amount of torque is 1,2 Nm. At the instant shown, the force gives to the disc the angular acceleration α = M/I = 7,5 rad/s2, and to its center of mass it gives the linear acceleration a = F/m = 4 m/s2.
. If the disc has the mass 0,5 kg and the radius 0,8 m, the moment of inertia is 0,16 kgm2. If the amount of force is 2 N, and the lever arm 0,6 m, the amount of torque is 1,2 Nm. At the instant shown, the force gives to the disc the angular acceleration α = M/I = 7,5 rad/s2, and to its center of mass it gives the linear acceleration a = F/m = 4 m/s2.Resultant force
Resultant force fully replaces the effects of all forces on the motion of the rigid body they act upon. When it can be determined, this is done in the following two steps:- First, vector addition is used to find the net force;
- Then the following torque equation specifies the position of its point of application:

where
 is the net force that becomes the resultant force when and if an appropriate position vector
is the net force that becomes the resultant force when and if an appropriate position vector  of its application point can be found; actual individual forces are denoted as
of its application point can be found; actual individual forces are denoted as  and their respective application points by
and their respective application points by  . All torques are calculated with respect to the same arbitrarily selected point.
. All torques are calculated with respect to the same arbitrarily selected point.The above equation may have no solution for
 . In that case there is no resultant force, i.e. no single force can replace all actual forces regarding both linear and angular acceleration of the body. And even when
. In that case there is no resultant force, i.e. no single force can replace all actual forces regarding both linear and angular acceleration of the body. And even when  can be calculated, it is not unique, because the point of application can move along the line of application without affecting the torque.
can be calculated, it is not unique, because the point of application can move along the line of application without affecting the torque.The diagram illustrates simple graphical methods for finding the line of application of the resultant force of simple planar systems.
- Lines of application of the actual forces
 and
and  on the leftmost illustration intersect. After vector addition is performed "at the location of
on the leftmost illustration intersect. After vector addition is performed "at the location of  ", the net force obtained is translated so that its line of application passes through the common intersection point. With respect to that point all torques are zero, so the torque of the resultant force
", the net force obtained is translated so that its line of application passes through the common intersection point. With respect to that point all torques are zero, so the torque of the resultant force  is equal to the sum of the torques of the actual forces.
is equal to the sum of the torques of the actual forces. - Illustration in the middle of the diagram shows two parallel actual forces. After vector addition "at the location of
 ", the net force is translated to the appropriate line of application, where it becomes the resultant force
", the net force is translated to the appropriate line of application, where it becomes the resultant force  . The procedure is based on decomposition of all forces into components for which the lines of application (pale dotted lines) intersect at one point (the so called pole, arbitrarily set at the right side of the illustration). Then the arguments from the previous case are applied to the forces and their components to demonstrate the torque relationships.
. The procedure is based on decomposition of all forces into components for which the lines of application (pale dotted lines) intersect at one point (the so called pole, arbitrarily set at the right side of the illustration). Then the arguments from the previous case are applied to the forces and their components to demonstrate the torque relationships. - The rightmost illustration shows a couple, two equal but opposite forces for which the amount of the net force is zero, but they produce the net torque
 where
where  is the distance between their lines of application. This is "pure" torque, since there is no resultant force.
is the distance between their lines of application. This is "pure" torque, since there is no resultant force.
Usage
Although the resultant force can be determined only for some configurations of forces, it is useful both conceptually and practically. When the system of forces can be replaced by a resultant force, this can simplify practical calculations (e.g. in many planar systems, or using the center of gravity in homogenous field, etc.). On the conceptual level, definition of the resultant force underlines the fact that the net force does not fully replace the system of forces (so, for example, the work of the net force cannot replace the net work in the case of an extended rigid body, e.g. in the work-energy theorem etc.). And the concept is also useful for a full understanding of a more general approach.Most generally, a system of forces acting on a rigid body can always be replaced by one force plus one "pure" torque. The force is the net force, but in order to calculate the additional torque, the net force must be assigned the line of action. The line of action can be selected arbitrarily, but the additional "pure" torque will depend on this choice. In the special case when it is possible to find such line of action that this additional torque is zero, the net force becomes the resultant force.
Some authors do not attribute any significance to this special case, particularly if they do not use it in practical calculations. Therefore, they do not distinguish the resultant force from the net force, i.e. they use the terms as synonyms, or arbitrarily use only one of them to denote the net force.

