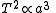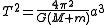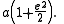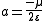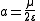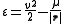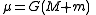Semi-major axis - AbsoluteAstronomy.com

The major axis of an ellipse

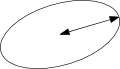
Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

is its longest diameter, a line that runs through the centre and both foci

Focus (geometry)

In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...

, its ends being at the widest points of the shape. The semi-major axis is one half of the major axis, and thus runs from the centre, through a focus

Focus (geometry)

, and to the edge of the ellipse; essentially, it is the measure of the radius of an orbit taken at the orbit's two most distant points. For the special case of a circle, the semi-major axis is the radius. One can think of the semi-major axis as an ellipse's long radius.

The length of the semi-major axis a of an ellipse is related to the semi-minor axis'

Semi-minor axis

In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...

length b through the eccentricity

Eccentricity (mathematics)

In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...

e and the semi-latus rectum ℓ, as follows:

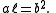
The semi-major axis of a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...

is, depending on the convention, plus or minus one half of the distance between the two branches. Thus it is the distance from the center to either vertex (turning point) of the hyperbola.

A parabola

Parabola

In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...

can be obtained as the limit of a sequence of ellipses where one focus is kept fixed as the other is allowed to move arbitrarily far away in one direction, keeping ℓ fixed. Thus

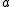and

tend to infinity, a faster than b.

Ellipse

The semi-major axis is the mean value of the smallest and largest distances from one focus to the points on the ellipse. Now consider the equation in polar coordinates, with one focus at the origin and the other on the positive x-axis,

The mean value of

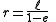and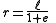

, (for

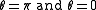) is

In an ellipse, the semimajor axis is the geometric mean

Geometric mean

The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...

of the distance from the center to either focus and the distance from the center to either directrix.

Hyperbola

In terms of the semi-latus rectum and the eccentricity we have

The transverse axis of a hyperbola coincides with the semi-major axis.

Orbital period

In astrodynamics

Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...

the orbital period

Orbital period

The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...

T of a small body orbiting a central body in a circular or elliptical orbit is:

where:

a is the length of the orbit's semi-major axis

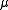is the standard gravitational parameter

Standard gravitational parameter

In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....

Note that for all ellipses with a given semi-major axis, the orbital period is the same, regardless of eccentricity.

The angular momentum

Angular momentum

In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...

H of a small body orbiting a central body in a circular or elliptical orbit is:

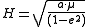
where:

a and

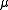are as defined above

e is the eccentricity of the orbit

In astronomy

Astronomy

Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...

, the semi-major axis is one of the most important orbital elements

Orbital elements

Orbital elements are the parameters required to uniquely identify a specific orbit. In celestial mechanics these elements are generally considered in classical two-body systems, where a Kepler orbit is used...

of an orbit

Orbit

In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...

, along with its orbital period

Orbital period

. For solar system

Solar System

The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...

objects, the semi-major axis is related to the period of the orbit by Kepler's third law

Kepler's laws of planetary motion

In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....

(originally empirical

Empirical

The word empirical denotes information gained by means of observation or experimentation. Empirical data are data produced by an experiment or observation....

ly derived),

where T is the period in years, and a is the semimajor axis in astronomical unit

Astronomical unit

An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....

s. This form turns out to be a simplification of the general form for the two-body problem

Two-body problem

In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...

, as determined by Newton

Isaac Newton

Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...

where G is the gravitational constant

Gravitational constant

The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

, and M is the mass

Mass

Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...

of the central body, and m is the mass of the orbiting body. Typically, the central body's mass is so much greater than the orbiting body's, that m may be ignored. Making that assumption and using typical astronomy units results in the simpler form Kepler discovered.

The orbiting body's path around the barycentre

Center of mass

In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...

and its path relative to its primary are both ellipses. The semi-major axis used in astronomy is always the primary-to-secondary distance; thus, the orbital parameters of the planets are given in heliocentric terms. The difference between the primocentric and "absolute" orbits may best be illustrated by looking at the Earth-Moon system. The mass ratio in this case is 81.30059. The Earth-Moon characteristic distance, the semi-major axis of the geocentric lunar orbit, is 384,400 km. The barycentric lunar orbit, on the other hand, has a semi-major axis of 379,700 km, the Earth's counter-orbit taking up the difference, 4,700 km. The Moon's average barycentric orbital speed is 1.010 km/s, whilst the Earth's is 0.012 km/s. The total of these speeds gives the geocentric lunar average orbital speed, 1.022 km/s; the same value may be obtained by considering just the geocentric semi-major axis value.

Average distance

It is often said that the semi-major axis is the "average" distance between the primary focus of the ellipse and the orbiting body. This is not quite precise, as it depends on what the average is taken over.

averaging the distance over the eccentric anomaly
Eccentric anomaly
In celestial mechanics, the eccentric anomaly is an angular parameter that defines the position of a body that is moving along an elliptic Kepler orbit.For the point P orbiting around an ellipse, the eccentric anomaly is the angle E in the figure...

(q.v.) indeed results in the semi-major axis.
averaging over the true anomaly
True anomaly
In celestial mechanics, the true anomaly is an angular parameter that defines the position of a body moving along a Keplerian orbit. It is the angle between the direction of periapsis and the current position of the body, as seen from the main focus of the ellipse .The true anomaly is usually...

(the true orbital angle, measured at the focus) results, oddly enough, in the semi-minor axis
Semi-minor axis
In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...

.
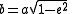averaging over the mean anomaly
Mean anomaly
In celestial mechanics, the mean anomaly is a parameter relating position and time for a body moving in a Kepler orbit. It is based on the fact that equal areas are swept at the focus in equal intervals of time....

(the fraction of the orbital period that has elapsed since pericentre, expressed as an angle), finally, gives the time-average

The time-average of the inverse of the radius, r⁻¹, is a⁻¹.

Energy; calculation of semi-major axis from state vectors

In astrodynamics

Astrodynamics

semi-major axis a can be calculated from orbital state vectors

Orbital state vectors

In astrodynamics or celestial dynamics orbital state vectors are vectors of position and velocity that together with their time uniquely determine the state of an orbiting body....

for an elliptical orbit and, depending on the convention, the same or

for a hyperbolic trajectory

Hyperbolic trajectory

In astrodynamics or celestial mechanics a hyperbolic trajectory is a Kepler orbit with the eccentricity greater than 1. Under standard assumptions a body traveling along this trajectory will coast to infinity, arriving there with hyperbolic excess velocity relative to the central body. Similarly to...

and

(specific orbital energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

)

and

(standard gravitational parameter

Standard gravitational parameter

), where:

v is orbital velocity from velocity vector of an orbiting object,
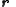is cartesian
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...

position vector of an orbiting object in coordinates of a reference frame
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

with respect to which the elements of the orbit are to be calculated (e.g. geocentric equatorial for an orbit around Earth, or heliocentric ecliptic for an orbit around the Sun),
G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...

,
M and m are the masses of the bodies.

Note that for a given amount of total mass, the specific energy and the semi-major axis are always the same, regardless of eccentricity or the ratio of the masses. Conversely, for a given total mass and semi-major axis, the total specific energy is always the same. This statement will always be true under any given conditions.

External links

Semi-major and semi-minor axes of an ellipse With interactive animation

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.