In differential calculus

Differential calculus

In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....

, an inflection point, point of inflection, or inflection (inflexion) is a point on a curve

Curve

In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...

 at which the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 or concavity changes sign

Sign (mathematics)

In mathematics, the word sign refers to the property of being positive or negative. Every nonzero real number is either positive or negative, and therefore has a sign. Zero itself is signless, although in some contexts it makes sense to consider a signed zero...

. The curve changes from being concave

Concave function

In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap or upper convex.-Definition:...

 upwards (positive curvature) to concave downwards (negative curvature), or vice versa. If one imagines driving a vehicle along a winding road, inflection is the point at which the steering-wheel is momentarily "straight" when being turned from left to right or vice versa.

Equivalent forms

The following are all equivalent to the above definition:

• a point on a curve at which the second derivative
  Second derivative
  In calculus, the second derivative of a function ƒ is the derivative of the derivative of ƒ. Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of a vehicle with respect to time is...
  
   changes sign. This is very similar to the previous definition, since the sign of the curvature is always the same as the sign of the second derivative, but note that the curvature
  Curvature
  In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
  
   is not the same as the second derivative
  Derivative
  In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
  
  .
• a point (x, y) on a function, f(x), at which the first derivative
  Derivative
  In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
  
  , f′(x), is at an extremum, i.e. a (local) minimum or maximum. (This is not the same as saying that y is at an extremum).
• a point on a curve
  Curve
  In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
  
   at which the tangent
  Tangent
  In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
  
   crosses the curve at that point. For an algebraic curve, this means a non singular point where the Multiplicity of the tangent line to the curve at p is greater than 2.

A necessary but not sufficient condition

If x is an inflection point for f then the second derivative, f″(x), is equal to zero if it exists, but this condition does not provide a sufficient definition of a point of inflection. One also needs the lowest-order non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection. (An example of such a function is y = x⁴).

It follows from the definition that the sign of f′(x) on either side of the point (x,y) must be the same. If this is positive, the point is a rising point of inflection; if it is negative, the point is a falling point of inflection.

Categorization of points of inflection

Points of inflection can also be categorised according to whether f′(x) is zero or not zero.

• if f′(x) is zero, the point is a stationary point
  Stationary point
  In mathematics, particularly in calculus, a stationary point is an input to a function where the derivative is zero : where the function "stops" increasing or decreasing ....
  
   of inflection, also known as a saddle-point
• if f′(x) is not zero, the point is a non-stationary point of inflection

An example of a saddle point is the point (0,0) on the graph y = x³. The tangent is the x-axis, which cuts the graph at this point.

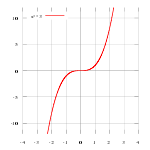
A non-stationary point of inflection can be visualised if the graph y = x³ is rotated slightly about the origin. The tangent at the origin still cuts the graph in two, but its gradient

Gradient

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....

 is non-zero.

Note that an inflection point is also called an ogee

Ogee

An ogee is a curve , shaped somewhat like an S, consisting of two arcs that curve in opposite senses, so that the ends are parallel....

, although this term is sometimes applied to the entire curve which contains an inflection point.

Asymptotic functions

Some functions change concavity without having points of inflection. Instead, they can change concavity around vertical asymptotes or discontinuities. Take, for example, the function . It is concave up when |x| > 1 and concave down when |x| < 1. However, it has no points of inflection because 1 and -1 are not in the domain of the function.

See also

• Critical point (mathematics)
  Critical point (mathematics)
  In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
  
  
• Vertex (curve)
  Vertex (curve)
  In the geometry of curves, a vertex is a point of where the first derivative of curvature is zero. This is typically a local maximum or minimum of curvature. Other special cases may occur, for instance when the second derivative is also zero, or when the curvature is constant...
  
  , a local minimum or maximum of curvature

External links

• Inflection Points of Fourth Degree Polynomials