Five points determine a conic
Encyclopedia
In geometry
, just as two (distinct) points determine a line
(a degree-1 plane curve), five points determine a conic (a degree-2 plane curve). There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.
Formally, given any five points in the plane in general linear position, meaning no three collinear, there is a unique conic passing through them, which will be non-degenerate; this is true over both the affine plane and projective plane
. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate
(reducible, because it contains a line), and may not be unique; see further discussion.
More precisely, this is seen as follows:
The two subtleties in the above analysis are that the resulting point is a quadratic equation (not a linear equation), and that the constraints are independent. The first is simple: if A, B, and C all vanish, then the equation
defines a line, and any 3 points on this (indeed any number of points) lie on a line – thus general linear position ensures a conic. The second, that the constraints are independent, is significantly subtler: it corresponds to the fact that given five points in general linear position in the plane, their images in 
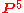under the Veronese map are in general linear position, which is true because the Veronese map is biregular – if the image of five points satisfy a relation, then the relation can be pulled back and the original points must also satisfy a relation. The Veronese map has coordinates 
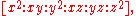and the target 
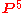is dual to the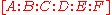 
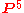of conics. The Veronese map corresponds to "evaluation of a conic at a point", and the statement about independence of constraints is exactly a geometric statement about this map.
– in terms of lines and points in the plane – in addition to the analytic (algebraic) proof given above. Such a proof can be given using a theorem of Jakob Steiner
, which states:
This can be shown by taking the points X and Y to the standard points
and 
by a projective transformation, in which case the pencils of lines correspond to the horizontal and vertical lines in the plane, and the intersections of corresponding lines to the graph of a function, which (must be shown) is a hyperbola, hence a conic, hence the original curve C is a conic.
Now given five points X, Y, A, B, C, the three lines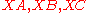
can be taken to the three lines 
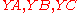by a unique projective transform, since projective transforms are simply 3-transitive on lines (they are simply 3-transitive on points, hence by projective duality they are 3-transitive on lines). Under this map A maps to B, since these are the unique intersection points of these lines, and thus satisfy the hypothesis of Steiner’s theorem. The resulting conic thus contains all five points, and is the unique such conic, as desired.
Analytically, the equation for the conic can be found by linear algebra
, by writing and solving the five equations in the coefficients: five equations, six unknowns, but homogeneous so scaling removes one dimension; concretely, setting one of the coefficients to 1 accomplishes this.
Synthetically, the conic can be constructed by the , by applying the Braikenridge–Maclaurin theorem
, which is the converse of Pascal's theorem
. Pascal's theorem states that given 6 points on a conic (a hexagon), the lines defined by opposite sides intersect in three collinear points. This can be reversed to construct the possible locations for a 6th point, given 5 existing ones.
.
A simple case of this is for a hypersurface
(a codimension
1 subvariety, the zeros of a single polynomial, the case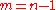
), of which plane curves are an example.
In the case of a hypersurface, the answer is given in terms of the multiset coefficient, more familiarly the binomial coefficient
, or more elegantly the rising factorial, as:
This is via the analogous analysis of the Veronese map: k points in general position impose k independent linear conditions on a variety (because the Veronese map is biregular), and the number of monomials of degree d in
variables (n-dimensional projective space has 
homogeneous coordinates) is 
from which 1 is subtracted because of projectivization: multiplying a polynomial by a constant does not change its zeros.
In the above formula, the number of points k is a polynomial in d of degree n, with leading coefficient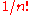
In the case of plane curves, where
the formula becomes:
whose values for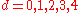
are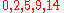 
– there are no curves of degree 0 (a single point is determines a point, which is codimension 2), 2 points determine a line, 5 points determine a conic, 9 points determine a cubic, 14 points determine a quartic, and so forth.
.
Conversely, four points do not determine a conic, but rather a pencil
, the 1-dimensional linear system of conics which all pass through the four points (formally, have the four points as base locus
). Similarly, three points determine a 2-dimensional linear system (net), two points determine a 3-dimensional linear system (web), one point determines a 4-dimensional linear system, and zero points place no constraints on the 5-dimensional linear system of all conics.
Fewer points are required to determine more specific conics – three points determine a circle
, while two points determine a pencil of circles, as in the Apollonian circles
.
Similarly, while nine points determine a cubic, if the nine points lie on more than one cubic – in other words, are the intersection of two cubics – then they are not in general position, and indeed satisfy an addition constraint, as stated in the Cayley–Bacharach theorem.
Another classic problem in enumerative geometry, of similar vintage to conics, is the Problem of Apollonius
– the requirement that a circle be tangent to three circles in general determines eight circles, as each of these is a quadratic condition and 23 = 8. As a question in real geometry, a full analysis involves many special cases, and the actual number of circles may be any number between 0 and 8, except for 7.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, just as two (distinct) points determine a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
(a degree-1 plane curve), five points determine a conic (a degree-2 plane curve). There are additional subtleties for conics that do not exist for lines, and thus the statement and its proof for conics are both more technical than for lines.
Formally, given any five points in the plane in general linear position, meaning no three collinear, there is a unique conic passing through them, which will be non-degenerate; this is true over both the affine plane and projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
. Indeed, given any five points there is a conic passing through them, but if three of the points are collinear the conic will be degenerate
Degenerate conic
In mathematics, a degenerate conic is a conic that fails to be an irreducible curve...
(reducible, because it contains a line), and may not be unique; see further discussion.
Proofs
This result can be proven numerous different ways; the dimension counting argument is most direct, and generalizes to higher degree, while other proofs are special to conics.Dimension counting
Intuitively, passing through five points in general linear position specifies five independent linear constraints on the (projective) linear space of conics, and hence specifies a unique conic, though this brief statement ignores subtleties.More precisely, this is seen as follows:
- conics correspond to points in the five-dimensional projective space
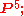
- requiring a conic to pass through a point imposes a linear condition on the coordinates: for a fixed
the equation 
is a linear equation in 
- by dimension counting five constraints (passing through five points) is necessary to specify a conic, as each constraints cuts the dimension of possibilities by 1, and one starts with 5 dimensions;
- in 5 dimensions, the intersection of 5 (independent) hyperplanes is a single point (formally, by Bézout's theoremBézout's theoremBézout's theorem is a statement in algebraic geometry concerning the number of common points, or intersection points, of two plane algebraic curves. The theorem claims that the number of common points of two such curves X and Y is equal to the product of their degrees...
); - general linear position of the points means that the constraints are independent, and thus do specify a unique conic;
- the resulting conic is non-degenerate because it is a curve (since it has more than 1 point), and does not contain a line (else it would split as two lines, at least one of which must contain 3 of the 5 points, by the pigeonhole principle), so it is irreducible.
The two subtleties in the above analysis are that the resulting point is a quadratic equation (not a linear equation), and that the constraints are independent. The first is simple: if A, B, and C all vanish, then the equation
defines a line, and any 3 points on this (indeed any number of points) lie on a line – thus general linear position ensures a conic. The second, that the constraints are independent, is significantly subtler: it corresponds to the fact that given five points in general linear position in the plane, their images in 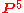under the Veronese map are in general linear position, which is true because the Veronese map is biregular – if the image of five points satisfy a relation, then the relation can be pulled back and the original points must also satisfy a relation. The Veronese map has coordinates 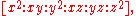and the target 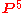is dual to the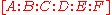 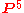of conics. The Veronese map corresponds to "evaluation of a conic at a point", and the statement about independence of constraints is exactly a geometric statement about this map.Synthetic proof
That five points determine a conic can be proven by synthetic geometrySynthetic geometry
Synthetic or axiomatic geometry is the branch of geometry which makes use of axioms, theorems and logical arguments to draw conclusions, as opposed to analytic and algebraic geometries which use analysis and algebra to perform geometric computations and solve problems.-Logical synthesis:The process...
– in terms of lines and points in the plane – in addition to the analytic (algebraic) proof given above. Such a proof can be given using a theorem of Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
, which states:
- Given a projective transformation f, between the pencil of lines passing through a point X and the pencil of lines passing through a point Y, the set C of intersection points between a line x and its image
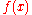forms a conic.
- Note that X and Y are on this conic by considering the preimage and image of the line XY (which is respectively a line through X and a line through Y).
This can be shown by taking the points X and Y to the standard points
and by a projective transformation, in which case the pencils of lines correspond to the horizontal and vertical lines in the plane, and the intersections of corresponding lines to the graph of a function, which (must be shown) is a hyperbola, hence a conic, hence the original curve C is a conic.Now given five points X, Y, A, B, C, the three lines
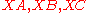can be taken to the three lines 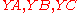by a unique projective transform, since projective transforms are simply 3-transitive on lines (they are simply 3-transitive on points, hence by projective duality they are 3-transitive on lines). Under this map A maps to B, since these are the unique intersection points of these lines, and thus satisfy the hypothesis of Steiner’s theorem. The resulting conic thus contains all five points, and is the unique such conic, as desired.Construction
Given five points, one can construct the conic containing them in various ways.Analytically, the equation for the conic can be found by linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
, by writing and solving the five equations in the coefficients: five equations, six unknowns, but homogeneous so scaling removes one dimension; concretely, setting one of the coefficients to 1 accomplishes this.
Synthetically, the conic can be constructed by the , by applying the Braikenridge–Maclaurin theorem
Braikenridge–Maclaurin theorem
In geometry, the ', named for 18th century British mathematicians William Braikenridge and Colin Maclaurin , is the converse to Pascal's theorem. It states that if the 3 intersection points of the lines through three sides of a hexagon lie on a line, then the 6 vertices of the hexagon lie on a...
, which is the converse of Pascal's theorem
Pascal's theorem
In projective geometry, Pascal's theorem states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.- Related results :This theorem...
. Pascal's theorem states that given 6 points on a conic (a hexagon), the lines defined by opposite sides intersect in three collinear points. This can be reversed to construct the possible locations for a 6th point, given 5 existing ones.
Generalizations
The natural generalization is to ask for what value of k a configuration of k points (in general position) in n-space determines a variety of degree d and dimension m, which is a fundamental question in enumerative geometryEnumerative geometry
In mathematics, enumerative geometry is the branch of algebraic geometry concerned with counting numbers of solutions to geometric questions, mainly by means of intersection theory.-History:...
.
A simple case of this is for a hypersurface
Hypersurface
In geometry, a hypersurface is a generalization of the concept of hyperplane. Suppose an enveloping manifold M has n dimensions; then any submanifold of M of n − 1 dimensions is a hypersurface...
(a codimension
Codimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
1 subvariety, the zeros of a single polynomial, the case
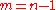), of which plane curves are an example.In the case of a hypersurface, the answer is given in terms of the multiset coefficient, more familiarly the binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
, or more elegantly the rising factorial, as:
This is via the analogous analysis of the Veronese map: k points in general position impose k independent linear conditions on a variety (because the Veronese map is biregular), and the number of monomials of degree d in
variables (n-dimensional projective space has homogeneous coordinates) is from which 1 is subtracted because of projectivization: multiplying a polynomial by a constant does not change its zeros.In the above formula, the number of points k is a polynomial in d of degree n, with leading coefficient
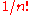
In the case of plane curves, where
the formula becomes:whose values for
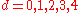are 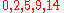– there are no curves of degree 0 (a single point is determines a point, which is codimension 2), 2 points determine a line, 5 points determine a conic, 9 points determine a cubic, 14 points determine a quartic, and so forth.Related results
While five points determine a conic, sets of six or more points on a conic are in special position, as demonstrated in Pascal's theoremPascal's theorem
In projective geometry, Pascal's theorem states that if an arbitrary hexagon is inscribed in any conic section, and pairs of opposite sides are extended until they meet, the three intersection points will lie on a straight line, the Pascal line of that configuration.- Related results :This theorem...
.
Conversely, four points do not determine a conic, but rather a pencil
Pencil (mathematics)
A pencil in projective geometry is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a projective plane....
, the 1-dimensional linear system of conics which all pass through the four points (formally, have the four points as base locus
Base locus
In mathematics, specifically algebraic geometry, the base locus of a linear system of divisors on a variety refers to the subvariety of points 'common' to all divisors in the linear system....
). Similarly, three points determine a 2-dimensional linear system (net), two points determine a 3-dimensional linear system (web), one point determines a 4-dimensional linear system, and zero points place no constraints on the 5-dimensional linear system of all conics.
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, while two points determine a pencil of circles, as in the Apollonian circles
Apollonian circles
Apollonian circles are two families of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates...
.
Similarly, while nine points determine a cubic, if the nine points lie on more than one cubic – in other words, are the intersection of two cubics – then they are not in general position, and indeed satisfy an addition constraint, as stated in the Cayley–Bacharach theorem.
Tangency
Instead of passing through points, a different condition on a curve is being tangent to a given line. Being tangent to five given lines also determines a conic, by projective duality, but from the algebraic point of view tangency to a line is a quadratic constraint, so naive dimension counting yields 25 = 32 conics tangent to five given lines, of which 31 must be ascribed to degenerate conics, as described in fudge factors in enumerative geometry; formalizing this intuition requires significant further development to justify.Another classic problem in enumerative geometry, of similar vintage to conics, is the Problem of Apollonius
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
– the requirement that a circle be tangent to three circles in general determines eight circles, as each of these is a quadratic condition and 23 = 8. As a question in real geometry, a full analysis involves many special cases, and the actual number of circles may be any number between 0 and 8, except for 7.
External links
- Five Points Determine a Conic Section, Wolfram interactive demonstration