
Hyperbolic angle
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a hyperbolic angle is a geometric figure that divides a hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. The science of hyperbolic angle parallels the relation of an ordinary angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
to a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
. The hyperbolic angle is first defined for a "standard position", and subsequently as a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
of an interval on a branch of a hyperbola.
A hyperbolic angle in standard position is the angle at (0, 0) between the ray to (1, 1) and the ray to (x, 1/x) where x > 1.
The magnitude of the hyperbolic angle is the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of the corresponding hyperbolic sector which is loge x.
Note that unlike circular angle, hyperbolic angle is unbounded, as is the function loge
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
x, a fact related to the unbounded nature of the harmonic series
Harmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
.
The hyperbolic angle in standard position is considered to be negative when 0 < x < 1.
Suppose ab = 1 and cd = 1 with c > a > 1 so that (a,b) and (c,d) determine an interval on the hyperbola xy = 1. Then the squeeze mapping
Squeeze mapping
In linear algebra, a squeeze mapping is a type of linear map that preserves Euclidean area of regions in the Cartesian plane, but is not a Euclidean motion.For a fixed positive real number r, the mapping →...
with diagonal elements b and a maps this interval to the standard position hyperbolic angle that runs from (1,1) to (bc,ad). By the result of Gregoire de Saint-Vincent
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
, the hyperbolic sector determined by (a,b) and (c,d) has the same area as this standard position angle, and the magnitude of the hyperbolic angle is taken to be this area.
The hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s sinh, cosh, and tanh use the hyperbolic angle as their independent variable
Dependent and independent variables
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
because their values may be premised on analogies to circular trigonometric functions when the hyperbolic angle defines a hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
.
Thus this parameter becomes one of the most useful in the calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
variable.
Comparison with circular angle
Hyperbolic angles can be motivated by considering a geometry (now usually called Pseudoeuclidean or Non-Euclidean geometry of spacetime) where, unlike Euclidean geometry, two directions are considered to be orthogonal not if they meet at 90° as in Euclidean geometry, but if they have reciprocal slopes (hyperbolic orthogonality).Whereas in Euclidean geometry moving steadily in an orthogonal direction to a ray from the origin traces out a circle, in pseudoeuclidean geometry steadily moving orthogonal to a ray from the origin traces out a hyperbola. In Euclidean space, the multiple of a given angle traces equal distances around a circle while it traces exponential distances upon the hyperbolic line.
Circular angles can be characterised geometrically by the property that the if two chords P0P1 and P0P2 subtend angles L1 and L2 at the centre of a circle, their sum L1 + L2 is the angle subtended by a chord PQ, where PQ is required to be parallel to P1P2.

Just as a point on a circular segment sweeps out an area proportional to the circular angle, so too it can be shown that with the above definition a point on a hyperbolic sector sweeps out an area proportional to the hyperbolic angle. A circle centred at (0,0) passing through (1,1) accumulates an area of 2π (since its radius is
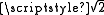 ). The same area units can also be used to give a scale to hyperbolic angles. It is notable that the hyperbola through (1,1) is always as far or further from the origin than the circle, so the hyperbolic angle for any ray emerging from the origin is always as large or larger than the same ray's circular angle.
). The same area units can also be used to give a scale to hyperbolic angles. It is notable that the hyperbola through (1,1) is always as far or further from the origin than the circle, so the hyperbolic angle for any ray emerging from the origin is always as large or larger than the same ray's circular angle.History
The quadratureQuadrature (mathematics)
Quadrature — historical mathematical term which means calculating of the area. Quadrature problems have served as one of the main sources of mathematical analysis.- History :...
of the hyperbola is the evaluation of the area swept out by a radial segment from the origin as the terminus moves along the hyperbola, just the topic of hyperbolic angle. The quadrature of the hyperbola was first accomplished by Gregoire de Saint-Vincent
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
in 1647 in his momentous Opus geometricum quadrature circuli et sectionum coni. As David Eugene Smith
David Eugene Smith
David Eugene Smith, Ph.D., LL.D. was an American mathematician, educator, and editor.-Education and career:...
wrote in 1925:
- [He made the] quadrature of a hyperbola to its asymptotes, and showed that as the area increased in arithmetic series the abscissas increased in geometric series.
- History of Mathematics, pp. 424,5 v. 1
The upshot was the logarithm function, as now understood as the area under y = 1/x to the right of x = 1. As an example of a transcendental function
Transcendental function
A transcendental function is a function that does not satisfy a polynomial equation whose coefficients are themselves polynomials, in contrast to an algebraic function, which does satisfy such an equation...
, the logarithm is more familiar than its motivator, the hyperbolic angle. Nevertheless, the hyperbolic angle plays a role when the theorem of Saint-Vincent is advanced with squeeze mapping.
Circular trigonometry was extended to the hyperbola in Augustus De Morgan
Augustus De Morgan
Augustus De Morgan was a British mathematician and logician. He formulated De Morgan's laws and introduced the term mathematical induction, making its idea rigorous. The crater De Morgan on the Moon is named after him....
's 1849 textbook Trigonometry and Double Algebra (see references for link). In 1878 W.K. Clifford used hyperbolic angle to parametrize a unit hyperbola
Unit hyperbola
In geometry, the unit hyperbola is the set of points in the Cartesian plane that satisfies x^2 - y^2 = 1 . In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial lengthWhereas the unit circle surrounds its center, the unit hyperbola requires the...
, describing it as "quasi-harmonic motion".
In 1894 Alexander Macfarlane
Alexander Macfarlane
Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....
circulated his essay "The Imaginary of Algebra", which used hyperbolic angles to generate hyperbolic versors, in his book Papers on Space Analysis.
When Ludwik Silberstein
Ludwik Silberstein
Ludwik Silberstein was a Polish-American physicist who helped make special relativity and general relativity staples of university coursework...
penned his popular 1914 textbook on the new theory of relativity, he used the rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
concept based on hyperbolic angle a where tanh a = v/c, the ratio of velocity v to the speed of light. He wrote:
- It seems worth mentioning that to unit rapidity corresponds a huge velocity, amounting to 3/4 of the velocity of light; more accurately we have v = (.7616) c for a = 1.
- ... the rapidity a = 1, ... consequently will represent the velocity .76 c which is a little above the velocity of light in water.
Silberstein also uses Lobachevsky's concept of angle of parallelism
Angle of parallelism
In hyperbolic geometry, the angle of parallelism φ, also known as Π, is the angle at one vertex of a right hyperbolic triangle that has two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism φ...
Π(a) to obtain cos Π(a) = v/c.
Imaginary circular angle
The hyperbolic angle is often presented as if it were an imaginary numberImaginary number
An imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
. In fact, if x is a real number and i2 = −1, then

so that the hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s cosh and sinh can be presented through the circular functions. But these identities do not arise from a circle or rotation, rather they can be understood in terms of infinite series. In particular, the one expressing the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
(
 ) consists of even and odd terms, the former comprise the cosh function (
) consists of even and odd terms, the former comprise the cosh function (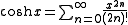 ), the latter the sinh function (
), the latter the sinh function ( ). The infinite series for cosine is derived from cosh by turning it into an alternating series. And the series for sine comes from making sinh into an alternating series. The above identities use the number i to remove the alternating factor (−1)n from terms of the series to restore the full halves of the exponential series. Nevertheless, in the theory of holomorphic function
). The infinite series for cosine is derived from cosh by turning it into an alternating series. And the series for sine comes from making sinh into an alternating series. The above identities use the number i to remove the alternating factor (−1)n from terms of the series to restore the full halves of the exponential series. Nevertheless, in the theory of holomorphic functionHolomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s, the hyperbolic sine and cosine functions are incorporated into the complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
sine and cosine functions.

