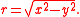Unit hyperbola
Encyclopedia
In geometry
, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfies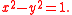
In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length
Whereas the unit circle
surrounds its center, the unit hyperbola requires the conjugate hyperbola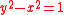
to complement it in the plane. This pair of hyperbolas share the asymptote
s y = x and y = −x. When the conjugate of the unit hyperbola is in use, the alternative radial length is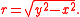
The unit hyperbola finds applications where the circle must be replaced with the hyperbola for purposes of analytic geometry. A prominent instance is the depiction of spacetime
as a pseudo-Euclidean space
. There the asymptotes of the unit hyperbola form a light cone
. Further, the attention to areas of hyperbolic sectors by Gregoire de Saint-Vincent
led to the logarithm function and the modern parametrization of the hyperbola by sector areas. When the notions of conjugate hyperbolas and hyperbolic angles are understood, then the classical complex number
s, which are built around the unit circle, can be replaced with numbers built around the unit hyperbola.
Each of these scales of coordinates results in photon
connections of events along diagonal lines of slope
plus or minus one.
Five elements constitute the diagram Herman Minkowski used to describe the relativity transformations: the unit hyperbola, its conjugate hyperbola, the axes of the hyperbola, a diameter of the unit hyperbola, and the conjugate diameter
.
The plane with the axes refers to a resting frame of reference
. The diameter of the unit hyperbola represents a frame of reference in motion with rapidity
a where
and (x,y) is the endpoint of the diameter on the unit hyperbola. The conjugate diameter represents the spatial hyperplane of simultaneity corresponding to rapidity a.
In this context the unit hyperbola is a calibration hyperbola
Commonly in relativity study the hyperbola with vertical axis is taken as primary:
The vertical time axis convention stems from Minkowski in 1908, and
is also illustrated on page 48 of Eddington's The Nature of the Physical World (1928).
, the hyperbola can be parametrized by the process of addition of points on a conic. The following description is given by Prasolov & Solovyev (1997):
This parameter is hyperbolic angle, being the argument of the hyperbolic function
s.
One finds an early expression of the parametrized unit hyperbola in Elements of Dynamic
(1878) by W. K. Clifford
. He describes quasi-harmonic motion in a hyperbola as follows:
s, the unit hyperbola is key to the split-complex number plane consisting of z = x + y j where j 2 = +1.
Then jz = y + x j so that the action of j on the plane is to swap the coordinates. In particular, this action swaps the unit hyperbola with its conjugate, and takes any hyperbola diameter to the conjugate diameter.
In terms of the hyperbolic angle parameter a, the unit hyperbola consists of points
where j = (0,1).
The right branch of the unit hyperbola corresponds to the positive coefficient. In fact, this branch is the image of the exponential function
acting on the j-axis. Since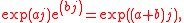
the branch is a group
under multiplication. Unlike the circle group, this unit hyperbola group is not compact
.
Similar to the ordinary complex plane, the elements have polar coordinates drawn from the parametrization of the unit hyperbola and the alternative radial length.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the unit hyperbola is the set of points (x,y) in the Cartesian plane that satisfies
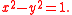In the study of indefinite orthogonal groups, the unit hyperbola forms the basis for an alternative radial length
Whereas the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
surrounds its center, the unit hyperbola requires the conjugate hyperbola
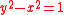to complement it in the plane. This pair of hyperbolas share the asymptoteAsymptote
In analytic geometry, an asymptote of a curve is a line such that the distance between the curve and the line approaches zero as they tend to infinity. Some sources include the requirement that the curve may not cross the line infinitely often, but this is unusual for modern authors...
s y = x and y = −x. When the conjugate of the unit hyperbola is in use, the alternative radial length is
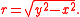
The unit hyperbola finds applications where the circle must be replaced with the hyperbola for purposes of analytic geometry. A prominent instance is the depiction of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
as a pseudo-Euclidean space
Pseudo-Euclidean space
A pseudo-Euclidean space is a finite-dimensional real vector space together with a non-degenerate indefinite quadratic form. Such a quadratic form can, after a change of coordinates, be written as...
. There the asymptotes of the unit hyperbola form a light cone
Light cone
A light cone is the path that a flash of light, emanating from a single event and traveling in all directions, would take through spacetime...
. Further, the attention to areas of hyperbolic sectors by Gregoire de Saint-Vincent
Grégoire de Saint-Vincent
Grégoire de Saint-Vincent , a Jesuit, was a mathematician who discovered that the area under a rectangular hyperbola is the same over [a,b] as over [c,d] when a/b = c/d...
led to the logarithm function and the modern parametrization of the hyperbola by sector areas. When the notions of conjugate hyperbolas and hyperbolic angles are understood, then the classical complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, which are built around the unit circle, can be replaced with numbers built around the unit hyperbola.
Minkowski diagram
The Minkowski diagram is drawn in a spacetime plane where the spatial aspect has been restricted to a single dimension. The units of distance and time on such a plane are- units of 30 centimetres length and nanosecondNanosecondA nanosecond is one billionth of a second . One nanosecond is to one second as one second is to 31.7 years.The word nanosecond is formed by the prefix nano and the unit second. Its symbol is ns....
s, or - astronomical unitAstronomical unitAn astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
s and intervals of 8 minutes and 20 seconds, or - light years and yearYearA year is the orbital period of the Earth moving around the Sun. For an observer on Earth, this corresponds to the period it takes the Sun to complete one course throughout the zodiac along the ecliptic....
s.
Each of these scales of coordinates results in photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
connections of events along diagonal lines of slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
plus or minus one.
Five elements constitute the diagram Herman Minkowski used to describe the relativity transformations: the unit hyperbola, its conjugate hyperbola, the axes of the hyperbola, a diameter of the unit hyperbola, and the conjugate diameter
Conjugate diameters
In geometry, two diameters of a conic section are said to be conjugate if each chord parallel to one diameter is bisected by the other diameter...
.
The plane with the axes refers to a resting frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
. The diameter of the unit hyperbola represents a frame of reference in motion with rapidity
Rapidity
In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...
a where
and (x,y) is the endpoint of the diameter on the unit hyperbola. The conjugate diameter represents the spatial hyperplane of simultaneity corresponding to rapidity a.In this context the unit hyperbola is a calibration hyperbola
Commonly in relativity study the hyperbola with vertical axis is taken as primary:
- The arrow of time goes from the bottom to top of the figure — a convention adopted by Richard Feyman in his famous dagrams. Space is represented by planes perpendicular to the time axis. The here and now is a singularity in the middle.
The vertical time axis convention stems from Minkowski in 1908, and
is also illustrated on page 48 of Eddington's The Nature of the Physical World (1928).
Parametrization
As a particular conicConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
, the hyperbola can be parametrized by the process of addition of points on a conic. The following description is given by Prasolov & Solovyev (1997):
- Fix a point E on the conic. Consider the points at which the straight line drawn through E parallel to AB intersects the conic a second time to be the sum of the points A and B.
- For the hyperbola
with the fixed point E = (1,0) the sum of the points 
and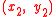 
is the point 
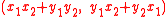under the parametrization 
and 
this addition corresponds to the addition of the parameter t .
This parameter is hyperbolic angle, being the argument of the hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s.
One finds an early expression of the parametrized unit hyperbola in Elements of Dynamic
Elements of Dynamic
Elements of Dynamic is a book published by William Kingdon Clifford in 1878. In 1887 it was supplemented by a fourth part and an appendix. The subtitle is "An introduction to motion and rest in solid and fluid bodies"...
(1878) by W. K. Clifford
W. K. Clifford
W. K. Clifford may refer to:*William Kingdon Clifford, British mathematician and philosopher*Lucy Clifford Mrs W. K. Clifford, wife of the above, British novelist and journalist...
. He describes quasi-harmonic motion in a hyperbola as follows:
- The motion
has some curious analogies to elliptic harmonic motion. ... The acceleration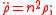 
thus it is always proportional to the distance from the centre, as in elliptic harmonic motion, but directed away from the centre.(pages 89, 90)
Complex plane algebra
Whereas the unit circle is associated with complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s, the unit hyperbola is key to the split-complex number plane consisting of z = x + y j where j 2 = +1.
Then jz = y + x j so that the action of j on the plane is to swap the coordinates. In particular, this action swaps the unit hyperbola with its conjugate, and takes any hyperbola diameter to the conjugate diameter.
In terms of the hyperbolic angle parameter a, the unit hyperbola consists of points
where j = (0,1).The right branch of the unit hyperbola corresponds to the positive coefficient. In fact, this branch is the image of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
acting on the j-axis. Since
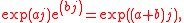
the branch is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
under multiplication. Unlike the circle group, this unit hyperbola group is not compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
.
Similar to the ordinary complex plane, the elements have polar coordinates drawn from the parametrization of the unit hyperbola and the alternative radial length.