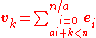Orthogonality
Encyclopedia
Mathematics
In mathematicsMathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
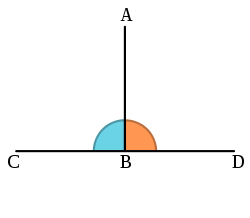
, two vectors are orthogonal if they are perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
, i.e., they form a right angle
Right angle
In geometry and trigonometry, a right angle is an angle that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles...
. The word comes from the Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
(orthos), meaning "straight", and (gonia), meaning "angle".
Definitions
- Two vectorsVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, and
and 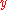 , in an inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, in an inner product spaceInner product spaceIn mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...
, , are orthogonal if their inner productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, are orthogonal if their inner productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
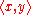 is zero. This relationship is denoted
is zero. This relationship is denoted 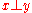 .
. - Two vector subspacesLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
, and
and  , of an inner product space,
, of an inner product space,  , are called orthogonal subspaces if each vector in
, are called orthogonal subspaces if each vector in  is orthogonal to each vector in
is orthogonal to each vector in  . The largest subspace of
. The largest subspace of  that is orthogonal to a given subspace is its orthogonal complement.
that is orthogonal to a given subspace is its orthogonal complement. - A linear transformationLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
,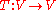 , is called an orthogonal linear transformation if it preserves the inner product. That is, for all pairs of vectors,
, is called an orthogonal linear transformation if it preserves the inner product. That is, for all pairs of vectors,  and
and 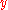 , in the inner product space
, in the inner product space  ,
,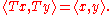
This means that
 preserves the angle
preserves the angleAngle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
between
 and
and 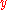 ,
,and that the length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
s of
 and
and  are equal.
are equal.A term rewriting system is said to be orthogonal
Orthogonality (term rewriting)
Orthogonality as a property of term rewriting systems describes where the reduction rules of the system are all left-linear, that is each variable occurs only once on the left hand side of each reduction rule, and there is no overlap between them....
if it is left-linear and is non-ambiguous. Orthogonal term rewriting systems are confluent
Confluence (term rewriting)
In computer science, confluence is a property of rewriting systems, describing that terms in this system can be rewritten in more than one way, to yield the same result. This article describes the properties in the most abstract setting of an abstract rewriting system.- Motivating example :Consider...
.
A set of vectors is called pairwise orthogonal if each pairing of them is orthogonal; such a set is called an orthogonal set. Non-zero pairwise orthogonal vectors are always linearly independent.
- Curves or functions in the plane are orthogonal if their tangent lines are perpendicular at their point of intersection.
The word normal is sometimes used in place of orthogonal. However, normal may also refer to unit vectors. In particular, an orthogonal set is called orthonormal if all its vectors are unit vectors. So, using the term normal to mean "orthogonal" is often avoided. Sometimes normal is used to describe a straight line that intersects a curve at a right angle. For example, the
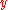 -axis is normal to the curve
-axis is normal to the curve 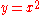 at the origin.
at the origin.Euclidean vector spaces
In 2- or higher-dimensionDimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, two vectors are orthogonal if their dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is zero, i.e. they make an angle of 90° or π/2 radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s. Hence orthogonality of vectors is an extension of the concept of perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
vectors into higher-dimensional spaces. In terms of Euclidean subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
s, the orthogonal complement of a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
is the plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
perpendicular to it, and vice versa. Note however that there is no correspondence with regards to perpendicular planes, because vectors in subspaces start from the origin
Origin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
.
In 4-dimensional Euclidean space, the orthogonal complement of a line is a hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
and vice versa, and that of a plane is a plane.
Orthogonal functions
It is common to use the following inner product for two functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
s f and g:
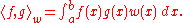
Here we introduce a nonnegative weight function
Weight function
A weight function is a mathematical device used when performing a sum, integral, or average in order to give some elements more "weight" or influence on the result than other elements in the same set. They occur frequently in statistics and analysis, and are closely related to the concept of a...
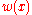 in the definition of this inner product.
in the definition of this inner product.We say that those functions are orthogonal if that inner product is zero:
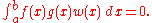
We write the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
s with respect to this inner product and the weight function as
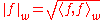
The members of a sequence { fi : i = 1, 2, 3, ... } are:
- orthogonal on the interval [a,b] if
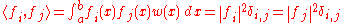
- orthonormal on the interval [a,b] if
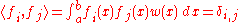
where
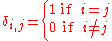
is the Kronecker delta. In other words, any two of them are orthogonal, and the norm of each is 1 in the case of the orthonormal sequence. See in particular orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
.
Examples
- The vectors (1, 3, 2), (3, −1, 0), (1/3, 1, −5/3) are orthogonal to each other, since (1)(3) + (3)(−1) + (2)(0) = 0, (3)(1/3) + (−1)(1) + (0)(−5/3) = 0, and (1)(1/3) + (3)(1) + (2)(−5/3) = 0.
- The vectors (1, 0, 1, 0, ...)T and (0, 1, 0, 1, ...)T are orthogonal to each other. The dot product of these vectors is 0. We can then make the generalization to consider the vectors in Z2n:
- for some positive integer a, and for 1 ≤ k ≤ a − 1, these vectors are orthogonal, for example (1, 0, 0, 1, 0, 0, 1, 0)T, (0, 1, 0, 0, 1, 0, 0, 1)T, (0, 0, 1, 0, 0, 1, 0, 0)T are orthogonal.
- Take two quadratic functions 2t + 3 and 5t2 + t − 17/9. These functions are orthogonal with respect to a unit weight function on the interval from −1 to 1. The product of these two functions is 10t3 + 17t2 − 7/9 t − 17/3, and now,
-

- The functions 1, sin(nx), cos(nx) : n = 1, 2, 3, ... are orthogonal with respect to Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the interval from 0 to 2π. This fact is central to the theory of Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
.
Orthogonal polynomials
- Various eponymously named polynomial sequences are sequences of orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
. In particular:- The Hermite polynomialsHermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
are orthogonal with respect to the normal distribution with expected value 0. - The Legendre polynomials are orthogonal with respect to the uniform distributionUniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on the interval from −1 to 1. - The Laguerre polynomialsLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
are orthogonal with respect to the exponential distributionExponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
. Somewhat more general Laguerre polynomial sequences are orthogonal with respect to gamma distributions. - The Chebyshev polynomialsChebyshev polynomialsIn mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
of the first kind are orthogonal with respect to the measure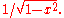
- The Chebyshev polynomials of the second kind are orthogonal with respect to the Wigner semicircle distribution.
- The Hermite polynomials
Orthogonal states in quantum mechanics
- In quantum mechanicsQuantum mechanicsQuantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, two eigenstates of a Hermitian operator,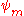 and
and 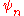 , are orthogonal if they correspond to different eigenvalues. This means, in Dirac notation, that
, are orthogonal if they correspond to different eigenvalues. This means, in Dirac notation, that 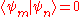 unless
unless 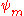 and
and 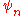 correspond to the same eigenvalue. This follows from the fact that Schrödinger's equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
correspond to the same eigenvalue. This follows from the fact that Schrödinger's equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
is a Sturm–Liouville equation (in Schrödinger's formulation) or that observables are given by hermitian operators (in Heisenberg's formulation).
Art and architecture
In art the perspectivePerspective (graphical)Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
imagined lines pointing to the vanishing pointVanishing pointA vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used...
are referred to as 'orthogonal lines'.
The term "orthogonal line" often has a quite different meaning in the literature of modern art criticism. Many works by painters such as Piet MondrianPiet MondrianPieter Cornelis "Piet" Mondriaan, after 1906 Mondrian , was a Dutch painter.He was an important contributor to the De Stijl art movement and group, which was founded by Theo van Doesburg. He evolved a non-representational form which he termed Neo-Plasticism...
and Burgoyne DillerBurgoyne DillerBurgoyne A. Diller was an American abstract painter. Many of his best-known works are characterized by orthogonal geometric forms that reflect his strong interest in the De Stijl movement and the work of Piet Mondrian in particular...
are noted for their exclusive use of "orthogonal lines" — not, however, with reference to perspective, but rather referring to lines which are straight and exclusively horizontal or vertical, forming right angles where they intersect. For example, an essay at the website of the Thyssen-Bornemisza Museum states that "Mondrian ....dedicated his entire oeuvre to the investigation of the balance between orthogonal lines and primary colours." http://www.museothyssen.org/thyssen_ing/coleccion/obras_ficha_texto_print497.html
Computer science
Orthogonality is a system design property facilitating feasibility and compactness of complex designs. Orthogonality guarantees that modifying the technical effect produced by a component of a system neither creates nor propagates side effects to other components of the system. The emergent behavior of a system consisting of components should be controlled strictly by formal definitions of its logic and not by side effects resulting from poor integration, i.e. non-orthogonal design of modules and interfaces. Orthogonality reduces testing and development time because it is easier to verify designs that neither cause side effects nor depend on them.
For example, a car has orthogonal components and controls (e.g. accelerating the vehicle does not influence anything else but the components involved exclusively with the acceleration function). On the other hand, a non-orthogonal design might have its steering influence its braking (e.g. electronic stability controlElectronic stability controlElectronic stability control is a computerized technology that may potentially improve the safety of a vehicle's stability by detecting and minimizing skids. When ESC detects loss of steering control, it automatically applies the brakes to help "steer" the vehicle where the driver intends to go...
), or its speed tweak its suspension. Consequently, this usage is seen to be derived from the use of orthogonal in mathematics: One may project a vector onto a subspaceLinear subspaceThe concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
by projecting it onto each member of a set of basis vectorsBasis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
separately and adding the projections if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the basis vectors are mutually orthogonal.
An instruction setInstruction setAn instruction set, or instruction set architecture , is the part of the computer architecture related to programming, including the native data types, instructions, registers, addressing modes, memory architecture, interrupt and exception handling, and external I/O...
is said to be orthogonal if it lacks redundancy (i.e. there is only a single instruction that can be used to accomplish a given task) and is designed such that instructions can use any registerProcessor registerIn computer architecture, a processor register is a small amount of storage available as part of a CPU or other digital processor. Such registers are addressed by mechanisms other than main memory and can be accessed more quickly...
in any addressing modeAddressing modeAddressing modes are an aspect of the instruction set architecture in most central processing unit designs. The various addressing modes that are defined in a given instruction set architecture define how machine language instructions in that architecture identify the operand of each instruction...
. This terminology results from considering an instruction as a vector whose components are the instruction fields. One field identifies the registers to be operated upon, and another specifies the addressing mode. An orthogonal instruction setOrthogonal instruction setOrthogonal instruction set is a term used in computer engineering. A computer's instruction set is said to be orthogonal if any instruction can use data of any type via any addressing mode...
uniquely encodes all combinations of registers and addressing modes.
Communications
In communications, multiple-access schemes are orthogonal when an ideal receiver can completely reject arbitrarily strong unwanted signals using different basis functionBasis functionIn mathematics, a basis function is an element of a particular basis for a function space. Every continuous function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be represented as a linear combination of basis...
s than the desired signal. One such scheme is TDMATime division multiple accessTime division multiple access is a channel access method for shared medium networks. It allows several users to share the same frequency channel by dividing the signal into different time slots. The users transmit in rapid succession, one after the other, each using its own time slot. This...
, where the orthogonal basis functions are non-overlapping rectangular pulses ("time slots").
Another scheme is orthogonal frequency-division multiplexingOrthogonal frequency-division multiplexingOrthogonal frequency-division multiplexing is a method of encoding digital data on multiple carrier frequencies. OFDM has developed into a popular scheme for wideband digital communication, whether wireless or over copper wires, used in applications such as digital television and audio...
(OFDM), which refers to the use, by a single transmitter, of a set of frequency multiplexed signals with the exact minimum frequency spacing needed to make them orthogonal so that they do not interfere with each other. Well known examples include (a, g, and n) versions of 802.11 Wi-FiWi-FiWi-Fi or Wifi, is a mechanism for wirelessly connecting electronic devices. A device enabled with Wi-Fi, such as a personal computer, video game console, smartphone, or digital audio player, can connect to the Internet via a wireless network access point. An access point has a range of about 20...
; WiMAXWiMAXWiMAX is a communication technology for wirelessly delivering high-speed Internet service to large geographical areas. The 2005 WiMAX revision provided bit rates up to 40 Mbit/s with the 2011 update up to 1 Gbit/s for fixed stations...
; ITU-TITU-TThe ITU Telecommunication Standardization Sector is one of the three sectors of the International Telecommunication Union ; it coordinates standards for telecommunications....
G.hnG.hnG.hn is the common name for a home network technology family of standards developed under the International Telecommunication Union's Standardization arm and promoted by the HomeGrid Forum...
, DVB-TDVB-TDVB-T is an abbreviation for Digital Video Broadcasting — Terrestrial; it is the DVB European-based consortium standard for the broadcast transmission of digital terrestrial television that was first published in 1997 and first broadcast in the UK in 1998...
, the terrestrial digital TV broadcast system used in most of the world outside North America; and DMT, the standard form of ADSL.
In OFDM, the sub-carrier frequencies are chosen so that the sub-carriers are orthogonal to each other, meaning that cross-talk between the sub-channels is eliminated and inter-carrier guard bands are not required. This greatly simplifies the design of both the transmitter and the receiver; unlike conventional FDM, a separate filter for each sub-channel is not required.
Statistics, econometrics, and economics
When performing statistical analysis, independent variablesDependent and independent variablesThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
that affect a particular dependent variableDependent and independent variablesThe terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
are said to be orthogonal if they are uncorrelated, since the covariance forms an inner product. In this case the same results are obtained for the effect of any of the independent variables upon the dependent variable, regardless of whether one models the variables' effects individually with simple regressionSimple linear regressionIn statistics, simple linear regression is the least squares estimator of a linear regression model with a single explanatory variable. In other words, simple linear regression fits a straight line through the set of n points in such a way that makes the sum of squared residuals of the model as...
or simultaneously with multiple regression. If correlationCorrelationIn statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
is present, the factors are not orthogonal and different results are obtained by the two methods. This usage arises from the fact that if centered (by subtracting the expected valueExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
(the mean)), uncorrelated variables are orthogonal in the geometric sense discussed above, both as observed data (i.e. vectors) and as random variables (i.e. density functions).
One econometricEconometricsEconometrics has been defined as "the application of mathematics and statistical methods to economic data" and described as the branch of economics "that aims to give empirical content to economic relations." More precisely, it is "the quantitative analysis of actual economic phenomena based on...
formalism that is alternative to the maximum likelihoodMaximum likelihoodIn statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
framework, the Generalized Method of MomentsGeneralized method of momentsIn econometrics, generalized method of moments is a generic method for estimating parameters in statistical models. Usually it is applied in the context of semiparametric models, where the parameter of interest is finite-dimensional, whereas the full shape of the distribution function of the data...
, relies on orthogonality conditions. In particular, the Ordinary Least SquaresOrdinary least squaresIn statistics, ordinary least squares or linear least squares is a method for estimating the unknown parameters in a linear regression model. This method minimizes the sum of squared vertical distances between the observed responses in the dataset and the responses predicted by the linear...
estimator may be easily derived from an orthogonality condition between dependent variables and model residuals.
Taxonomy
In taxonomyTaxonomyTaxonomy is the science of identifying and naming species, and arranging them into a classification. The field of taxonomy, sometimes referred to as "biological taxonomy", revolves around the description and use of taxonomic units, known as taxa...
, an orthogonal classification is one in which no item is a member of more than one group, that is, the classifications are mutually exclusive.
Combinatorics
In combinatoricsCombinatoricsCombinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, two n×n Latin squares are said to be orthogonal if their superimpositionSuperimpositionIn graphics, superimposition is the placement of an image or video on top of an already-existing image or video, usually to add to the overall image effect, but also sometimes to conceal something .This technique is used in cartography to produce photomaps by superimposing grid lines, contour lines...
yields all possible n2 combinations of entries.
Chemistry
In synthetic organic chemistryOrganic synthesisOrganic synthesis is a special branch of chemical synthesis and is concerned with the construction of organic compounds via organic reactions. Organic molecules can often contain a higher level of complexity compared to purely inorganic compounds, so the synthesis of organic compounds has...
orthogonal protectionProtecting groupA protecting group or protective group is introduced into a molecule by chemical modification of a functional group in order to obtain chemoselectivity in a subsequent chemical reaction...
is a strategy allowing the deprotection of functional groupFunctional groupIn organic chemistry, functional groups are specific groups of atoms within molecules that are responsible for the characteristic chemical reactions of those molecules. The same functional group will undergo the same or similar chemical reaction regardless of the size of the molecule it is a part of...
s independently of each other.
System Reliability
In the field of system reliability orthogonal redundancy is that form of redundancy where the form of backup device or method is completely different from the prone to error device or method. The failure mode of an orthogonally redundant backup device or method does not intersect with and is completely different from the failure mode of the device or method in need of redundancy to safeguard the total system against catastrophic failure.
Neuroscience
In neuroscienceNeuroscienceNeuroscience is the scientific study of the nervous system. Traditionally, neuroscience has been seen as a branch of biology. However, it is currently an interdisciplinary science that collaborates with other fields such as chemistry, computer science, engineering, linguistics, mathematics,...
, a sensory map in the brain which has overlapping stimulus coding (e.g. location and quality) is called an orthogonal map.
See also
- Orthogonalization
- Gram–Schmidt processGram–Schmidt processIn mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalising a set of vectors in an inner product space, most commonly the Euclidean space Rn...
- Gram–Schmidt process
- Orthogonal complement
- OrthonormalityOrthonormalityIn linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
- Pan-orthogonality occurs in coquaternionCoquaternionIn abstract algebra, the split-quaternions or coquaternions are elements of a 4-dimensional associative algebra introduced by James Cockle in 1849 under the latter name. Like the quaternions introduced by Hamilton in 1843, they form a four dimensional real vector space equipped with a...
s - Orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
- Orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
- Orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
- Orthogonal groupOrthogonal groupIn mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
- Surface normalSurface normalA surface normal, or simply normal, to a flat surface is a vector that is perpendicular to that surface. A normal to a non-flat surface at a point P on the surface is a vector perpendicular to the tangent plane to that surface at P. The word "normal" is also used as an adjective: a line normal to a...
- Imaginary numberImaginary numberAn imaginary number is any number whose square is a real number less than zero. When any real number is squared, the result is never negative, but the square of an imaginary number is always negative...
- IsogonalIsogonalIsogonal is a mathematical term which means "having similar angles". It occurs in several contexts:*Isogonal polygon, polyhedron, polytope or tiling.*Isogonal trajectory in curve theory.*Isogonal conjugate in triangle geometry....
- Isogonal trajectoryIsogonal trajectoryWhen a family of curves intersects another family at a specific constant angle α, the first family is referred to as an isogonal family of the second one, and in this case it is said that every family is an isogonal trajectory of the other. It is assumed that α is different from π/2; if α=π/2 both...
- The functions 1, sin(nx), cos(nx) : n = 1, 2, 3, ... are orthogonal with respect to Lebesgue measure