
Basis function
Encyclopedia
In mathematics
, a basis function is an element of a particular basis
for a function space
. Every continuous function in the function space can be represented as a linear combination
of basis functions, just as every vector in a vector space
can be represented as a linear combination of basis vectors.
In numerical analysis
and approximation theory
, basis functions are also called blending functions, because of their use in interpolation
: In this application, a mixture of the basis functions provides an interpolating function (with the "blend" depending on the evaluation of the basis functions at the data points).
of the basis functions 1, t, and t2. The set {(1/2)(t-1)(t-2), -t(t-2), (1/2)t(t-1)} is another basis for quadratic polynomials, called the Lagrange basis
.
) Schauder basis
for square-integrable functions. As a particular example, the collection: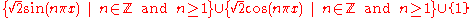
forms a basis for L2(0,1).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a basis function is an element of a particular basis
Basis (linear algebra)
In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
for a function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
. Every continuous function in the function space can be represented as a linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of basis functions, just as every vector in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
can be represented as a linear combination of basis vectors.
In numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
and approximation theory
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, basis functions are also called blending functions, because of their use in interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
: In this application, a mixture of the basis functions provides an interpolating function (with the "blend" depending on the evaluation of the basis functions at the data points).
Polynomial bases
The collection of quadratic polynomials with real coefficients has {1, t, t2} as a basis. Every quadratic polynomial can be written as a1+bt+ct2, that is, as a linear combinationLinear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the basis functions 1, t, and t2. The set {(1/2)(t-1)(t-2), -t(t-2), (1/2)t(t-1)} is another basis for quadratic polynomials, called the Lagrange basis
Lagrange polynomial
In numerical analysis, Lagrange polynomials are used for polynomial interpolation. For a given set of distinct points x_j and numbers y_j, the Lagrange polynomial is the polynomial of the least degree that at each point x_j assumes the corresponding value y_j...
.
Fourier basis
Sines and cosines form an (orthonormalOrthonormality
In linear algebra, two vectors in an inner product space are orthonormal if they are orthogonal and both of unit length. A set of vectors form an orthonormal set if all vectors in the set are mutually orthogonal and all of unit length...
) Schauder basis
Schauder basis
In mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
for square-integrable functions. As a particular example, the collection:
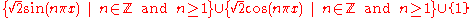
forms a basis for L2(0,1).
See also
- Basis (linear algebra)Basis (linear algebra)In linear algebra, a basis is a set of linearly independent vectors that, in a linear combination, can represent every vector in a given vector space or free module, or, more simply put, which define a "coordinate system"...
(Hamel basis) - Schauder basisSchauder basisIn mathematics, a Schauder basis or countable basis is similar to the usual basis of a vector space; the difference is that Hamel bases use linear combinations that are finite sums, while for Schauder bases they may be infinite sums...
(in a Banach spaceBanach spaceIn mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
) - Dual basis
- Biorthogonal system (Markushevich basis)
- Orthonormal basisOrthonormal basisIn mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
in an inner-product space - Orthogonal polynomialsOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
- Fourier analysis and Fourier seriesFourier seriesIn mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
- Harmonic analysisHarmonic analysisHarmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
- Orthogonal waveletOrthogonal waveletAn orthogonal wavelet is a wavelet where the associated wavelet transform is orthogonal.That is the inverse wavelet transform is the adjoint of the wavelet transform.If this condition is weakened you may end up with biorthogonal wavelets.- Basics :...
- Biorthogonal waveletBiorthogonal waveletA biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets...
- Radial basis functionRadial basis functionA radial basis function is a real-valued function whose value depends only on the distance from the origin, so that \phi = \phi; or alternatively on the distance from some other point c, called a center, so that \phi = \phi...
- Finite-elements (bases)
- Functional analysisFunctional analysisFunctional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
- Approximation theoryApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
- Numerical analysisNumerical analysisNumerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

