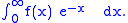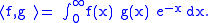
Laguerre polynomials
Overview
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Laguerre polynomials, named after Edmond Laguerre
Edmond Laguerre
Edmond Nicolas Laguerre was a French mathematician, a member of the Académie française . His main works were in the areas of geometry and complex analysis. He also investigated orthogonal polynomials...
(1834 – 1886),
are the canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
solutions of Laguerre's equation:
-

which is a second-order linear differential equationLinear differential equationLinear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
.
This equation has nonsingular solutions only if n is a non-negative integer. The Laguerre polynomials are also used for Gaussian quadratureGaussian quadratureIn numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....
to numerically compute integrals of the form
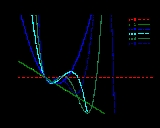
These polynomials, usually denoted L0, L1, ..., are a polynomial sequencePolynomial sequenceIn mathematics, a polynomial sequence is a sequence of polynomials indexed by the nonnegative integers 0, 1, 2, 3, ..., in which each index is equal to the degree of the corresponding polynomial...
which may be defined by the Rodrigues formula
-
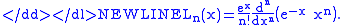
They are orthogonalOrthogonal polynomialsIn mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
to each other with respect to the inner product given by
The sequence of Laguerre polynomials is a Sheffer sequence.
The rook polynomials in combinatorics are more or less the same as Laguerre polynomials, up to elementary changes of variables.
The Laguerre polynomials arise in quantum mechanics, in the radial part of the solution
of the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a one-electron atom.
Physicists often use a definition for the Laguerre polynomials that is larger,
by a factor of n! , than the definition used here. -
-
Unanswered Questions