
Perspective (graphical)
Encyclopedia

- Smaller as their distance from the observer increases
- Foreshortened: the size of an object's dimensions along the line of sight are relatively shorter than dimensions across the line of sight
Overview
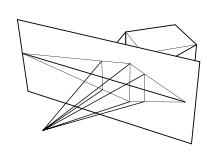
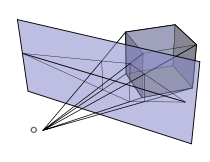
Depth perception
Depth perception is the visual ability to perceive the world in three dimensions and the distance of an object. Depth sensation is the ability to move accurately, or to respond consistently, based on the distances of objects in an environment....
) any difference between the painted scene on the windowpane and the view of the real scene.
All perspective drawings assume the viewer is a certain distance away from the drawing. Objects are scaled relative to that viewer. Additionally, an object is often not scaled evenly: a circle often appears as an ellipse and a square can appear as a trapezoid. This distortion is referred to as foreshortening.
Perspective drawings typically have an -often implied- horizon line. This line, directly opposite the viewer's eye, represents objects infinitely far away. They have shrunk, in the distance, to the infinitesimal thickness of a line. It is analogous to (and named after) the Earth's horizon
Horizon
The horizon is the apparent line that separates earth from sky, the line that divides all visible directions into two categories: those that intersect the Earth's surface, and those that do not. At many locations, the true horizon is obscured by trees, buildings, mountains, etc., and the resulting...
.
Any perspective representation of a scene that includes parallel lines has one or more vanishing point
Vanishing point
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used...
s in a perspective drawing. A one-point perspective drawing means that the drawing has a single vanishing point, usually (though not necessarily) directly opposite the viewer's eye and usually (though not necessarily) on the horizon line. All lines parallel with the viewer's line of sight recede to the horizon towards this vanishing point. This is the standard "receding railroad tracks" phenomenon. A two-point drawing would have lines parallel to two different angles. Any number of vanishing points are possible in a drawing, one for each set of parallel lines that are at an angle relative to the plane of the drawing.
Perspectives consisting of many parallel lines are observed most often when drawing architecture (architecture frequently uses lines parallel to the x, y, and z axes
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
). Because it is rare to have a scene consisting solely of lines parallel to the three Cartesian axes (x, y, and z), it is rare to see perspectives in practice with only one, two, or three vanishing points; even a simple house frequently has a peaked roof which results in a minimum of six sets of parallel lines, in turn corresponding to up to six vanishing points.
In contrast, natural scenes often do not have any sets of parallel lines. Such a perspective would thus have no vanishing points.
Early history
The earliest art paintings and drawings typically sized objects and characters hieratically according to their spiritual or thematic importance, not their distance from the viewer, and did not use foreshortening. The most important figures are often shown as the highest in a composition, also from hieratic motives, leading to the "vertical perspective", common in the art of Ancient EgyptArt of Ancient Egypt
Ancient Egyptian art is the painting, sculpture, architecture and other arts produced by the civilization in the lower Nile Valley from 5000 BC to 300 AD. Ancient Egyptian art reached a high level in painting and sculpture, and was both highly stylized and symbolic...
, where a group of "nearer" figures are shown below the larger figure or figures. The only method to indicate the relative position of elements in the composition was by overlapping, of which much use is made in works like the Parthenon Marbles.


Anaxagoras
Anaxagoras was a Pre-Socratic Greek philosopher. Born in Clazomenae in Asia Minor, Anaxagoras was the first philosopher to bring philosophy from Ionia to Athens. He attempted to give a scientific account of eclipses, meteors, rainbows, and the sun, which he described as a fiery mass larger than...
and Democritus
Democritus
Democritus was an Ancient Greek philosopher born in Abdera, Thrace, Greece. He was an influential pre-Socratic philosopher and pupil of Leucippus, who formulated an atomic theory for the cosmos....
worked out geometric theories of perspective for use with skenographia. Alcibiades
Alcibiades
Alcibiades, son of Clinias, from the deme of Scambonidae , was a prominent Athenian statesman, orator, and general. He was the last famous member of his mother's aristocratic family, the Alcmaeonidae, which fell from prominence after the Peloponnesian War...
had paintings in his house designed based on skenographia, thus this art was not confined merely to the stage. Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
's Optics
Euclid's Optics
Euclid's Optics, is a work on the geometry of vision written by the Greek mathematician Euclid around 300 BC. The earliest surviving manuscript of Optics is in Greek and dates from the 10th century AD....
introduced a mathematical theory of perspective; however, there is some debate over the extent to which Euclid's perspective coincides with a modern mathematical definition of perspective.
By the later periods of antiquity artists, especially those in less popular traditions, were well aware that distant objects could be shown smaller than those close at hand for increased illusionism, but whether this convention was actually used in a work depended on many factors.
Some of the paintings found in the ruins of Pompeii
House of the Vettii
In Pompeii one of the most famous of the luxurious residences is the so-called House of the Vettii, preserved like the rest of the Roman city by the eruption of Vesuvius in 79 AD. The house is named for its owners, two successful freedmen: Aulus Vettius Conviva, an Augustalis, and Aulus Vettius...
show a remarkable realism and perspective for their time; it has been claimed that comprehensive systems of perspective were evolved in antiquity, but most scholars do not accept this. Hardly any of the many works where such a system would have been used have survived. A passage in Philostratus suggests that classical artists and theorists thought in terms of "circles" at equal distance from the viewer, like a classical semi-circular theatre seen from the stage. The roof beams in rooms in the Vatican Virgil, from about 400 AD, are shown converging, more or less, on a common vanishing point, but this is not systematically related to the rest of the composition. In the Late Antique period use of perspective techniques declined. The art of the new cultures of the Migration Period
Migration Period
The Migration Period, also called the Barbarian Invasions , was a period of intensified human migration in Europe that occurred from c. 400 to 800 CE. This period marked the transition from Late Antiquity to the Early Middle Ages...
had no tradition of attempting compositions of large numbers of figures and Early Medieval art was slow and inconsistent in relearning the convention from classical models, though the process can be seen underway in Carolingian art
Carolingian art
Carolingian art comes from the Frankish Empire in the period of roughly 120 years from about AD 780 to 900 — during the reign of Charlemagne and his immediate heirs — popularly known as the Carolingian Renaissance. The art was produced by and for the court circle and a group of...
.
European Medieval artists were aware of the general principle of varying the relative size of elements according to distance, but even more than classical art was perfectly ready to override it for other reasons. Buildings were often shown obliquely according to a particular convention. The use and sophistication of attempts to convey distance increased steadily during the period, but without a basis in a systematic theory. Byzantine art
Byzantine art
Byzantine art is the term commonly used to describe the artistic products of the Byzantine Empire from about the 5th century until the Fall of Constantinople in 1453....
was also aware of these principles, but also had the reverse perspective
Reverse perspective
Reverse perspective, also called inverse perspective, inverted perspective or Byzantine perspective, is a convention of perspective drawing where the further the objects are, the larger they are drawn. The lines diverge against the horizon, rather than converge as in linear perspective...
convention for the setting of principal figures.
Giotto attempted drawings in perspective using an algebraic method to determine the placement of distant lines. The problem with using a linear ratio in this manner is that the apparent distance between a series of evenly spaced lines actually falls off with a sine
Sine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
dependence. To determine the ratio for each succeeding line, a recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
ratio must be used.
One of Giotto's first uses of his algebraic method of perspective was Jesus Before Caiaphas. Although the picture does not conform to the modern, geometrical method of perspective, it does give a considerable illusion of depth, and was a large step forward in Western art.
With the exception of dice, heraldry
Heraldry
Heraldry is the profession, study, or art of creating, granting, and blazoning arms and ruling on questions of rank or protocol, as exercised by an officer of arms. Heraldry comes from Anglo-Norman herald, from the Germanic compound harja-waldaz, "army commander"...
typically ignores perspective in the treatment of charges
Charge (heraldry)
In heraldry, a charge is any emblem or device occupying the field of an escutcheon . This may be a geometric design or a symbolic representation of a person, animal, plant, object or other device...
, though sometimes in later centuries charges are specified as in perspective.
Renaissance : Mathematical basis
Prior to the RenaissanceRenaissance
The Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
, Alhazen (al-Hasan Ibn al-Haytham, d. ca. 1041 AD), in his Book of Optics
Book of Optics
The Book of Optics ; ; Latin: De Aspectibus or Opticae Thesaurus: Alhazeni Arabis; Italian: Deli Aspecti) is a seven-volume treatise on optics and other fields of study composed by the medieval Muslim scholar Alhazen .-See also:* Science in medieval Islam...
(Kitab al-manazir; known in Latin as De aspectibus or Perspectiva, written in 1021), explained that light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
projects conically into the eye. Alhazen's geometrical, physical, physio-psychological optics resolved in this the ancient dispute between the mathematicians (Ptolemaic and Euclidean) and the physicists (Aristotelian) over the nature of vision and light. He also showed that vision is not merely a phenomenon of pure sensation (namely what results from the introduction of light rays into the eyes), but that it involves the faculties of judgment, imagination and memory. Alhazen's geometrical model of the cone of vision was theoretically sufficient to translate visible objects within a given setting into a painting, and this was also supported by his experimental affirmation of the visibility of spatial depth; hence of offering a proper ground for the idea of perspective. Moreover, Alhazen presented a geometrical conception of place as spatial extension (a postulated void), and he refuted the Aristotelian account of topos as a surface of containment. Alhazen's mathematical definition of place was more akin to Plato's notion of Khôra or Chora
Chora
Chora can mean one of several things:Localities* Chora District in the Uruzgan province of Afghanistan* Chora , a district in the Oromia Region of Ethiopia* The Chora Church, a Byzantine church in Istanbul...
as 'space', yet conceived on pure geometric grounds to facilitate the use of projections. In all of this, Alhazen was concerned with optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
, with vision, light and the nature of colour, as well as with experimentation and the use of optical instruments, and not with painting as such. Conical translations are mathematically difficult, so a drawing constructed using them would be incredibly time consuming. However, what Alhazen named a cone of vision (makhrut al-shu'a) corresponded also with the idea of a pyramid of vision, hence, offering a model that can be more easily projected in orthogonal drawings of side views and top views that are needed in the geometric construction of perspective.
By the 14th century, Alhazen's Book of Optics was available in Italian
Italian language
Italian is a Romance language spoken mainly in Europe: Italy, Switzerland, San Marino, Vatican City, by minorities in Malta, Monaco, Croatia, Slovenia, France, Libya, Eritrea, and Somalia, and by immigrant communities in the Americas and Australia...
translation, entitled Deli Aspecti. The Renaissance artist Lorenzo Ghiberti
Lorenzo Ghiberti
Lorenzo Ghiberti , born Lorenzo di Bartolo, was an Italian artist of the early Renaissance best known for works in sculpture and metalworking.-Early life:...
relied heavily upon this work, quoting it "verbatim and at length" while framing his account of art and its aesthetic imperatives in the “Commentario terzo.” Alhazen’s work was thus "central to the development of Ghiberti’s thought about art and visual aesthetics" and "may well have been central to the development of artificial perspective in early Renaissance Italian painting."
In about 1413 a contemporary of Ghiberti, Filippo Brunelleschi
Filippo Brunelleschi
Filippo Brunelleschi was one of the foremost architects and engineers of the Italian Renaissance. He is perhaps most famous for inventing linear perspective and designing the dome of the Florence Cathedral, but his accomplishments also included bronze artwork, architecture , mathematics,...
, demonstrated the geometrical method of perspective, used today by artists, by painting the outlines of various Florentine buildings onto a mirror. When the building's outline was continued, he noticed that all of the lines converged on the horizon line. According to Vasari, he then set up a demonstration of his painting of the Baptistery
Battistero di San Giovanni (Florence)
The Florence Baptistry or Battistero di San Giovanni is a religious building in Florence , Italy, which has the status of a minor basilica....
in the incomplete doorway of the Duomo
Santa Maria del Fiore
The Basilica di Santa Maria del Fiore is the cathedral church of Florence, Italy. The Duomo, as it is ordinarily called, was begun in 1296 in the Gothic style to the design of Arnolfo di Cambio and completed structurally in 1436 with the dome engineered by Filippo Brunelleschi...
. He had the viewer look through a small hole on the back of the painting, facing the Baptistery. He would then set up a mirror, facing the viewer, which reflected his painting. To the viewer, the painting of the Baptistery and the Baptistery itself were nearly indistinguishable.
Soon after, nearly every artist in Florence and in Italy used geometrical perspective in their paintings, notably Masolino da Panicale
Masolino da Panicale
Masolino da Panicale was an Italian painter. His best known works are probably his collaborations with Masaccio: Madonna with Child and St. Anne and the frescoes in the Brancacci Chapel .-Biography:Masolino was born in Panicale...
and Donatello
Donatello
Donato di Niccolò di Betto Bardi , also known as Donatello, was an early Renaissance Italian artist and sculptor from Florence...
. Donatello started sculpting elaborate checkerboard floors into the simple manger
Manger
A manger is a trough or box of carved stone or wood construction used to hold food for animals . Mangers are mostly used in livestock raising. They are also used to feed wild animals, e.g., in nature reserves...
portrayed in the birth of Christ. Although hardly historically accurate, these checkerboard floors obeyed the primary laws of geometrical perspective: the lines converged approximately to a vanishing point, and the rate at which the horizontal lines receded into the distance was graphically determined. This became an integral part of Quattrocento
Quattrocento
The cultural and artistic events of 15th century Italy are collectively referred to as the Quattrocento...
art. Melozzo da Forlì
Melozzo da Forlì
Melozzo da Forlì was an Italian Renaissance painter and architect. His fresco paintings are notable for the use of foreshortening. He was the most important member of the Forlì painting school.- Biography :...
first used the technique of upward foreshortening (in Rome
Rome
Rome is the capital of Italy and the country's largest and most populated city and comune, with over 2.7 million residents in . The city is located in the central-western portion of the Italian Peninsula, on the Tiber River within the Lazio region of Italy.Rome's history spans two and a half...
, Loreto
Loreto (AN)
Loreto is a hilltown and comune of the Italian province of Ancona, in the Marche. It is mostly famous as the seat of the Basilica della Santa Casa, a popular Catholic pilgrimage site.-Location:...
, Forlì
Forlì
Forlì is a comune and city in Emilia-Romagna, Italy, and is the capital of the province of Forlì-Cesena. The city is situated along the Via Emilia, to the right of the Montone river, and is an important agricultural centre...
and others), and was celebrated for that. Not only was perspective a way of showing depth, it was also a new method of composing
Composition (visual arts)
In the visual arts – in particular painting, graphic design, photography and sculpture – composition is the placement or arrangement of visual elements or ingredients in a work of art or a photograph, as distinct from the subject of a work...
a painting. Paintings began to show a single, unified scene, rather than a combination of several.


Paolo dal Pozzo Toscanelli
Paolo dal Pozzo Toscanelli was an Italian mathematician, astronomer, and cosmographer.-Life:Paolo dal Pozzo Toscanelli was born in Florence, the son of the physician Dominic Toscanelli. Educated in mathematics at the University of Padua, he left in 1424 with the title of a doctor of...
), but did not publish, the mathematics behind perspective. Decades later, his friend Leon Battista Alberti wrote De pictura
De pictura
De pictura is a treatise on painting written in 1435 by Italian architect and art theorist Leon Battista Alberti. It was first published in Italian in 1436...
(1435/1436), a treatise on proper methods of showing distance in painting. Alberti's primary breakthrough was not to show the mathematics in terms of conical projections, as it actually appears to the eye. Instead, he formulated the theory based on planar projections, or how the rays of light, passing from the viewer's eye to the landscape, would strike the picture plane (the painting). He was then able to calculate the apparent height of a distant object using two similar triangles. The mathematics behind similar triangles is relatively simple, having been long ago formulated by Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
. In viewing a wall, for instance, the first triangle has a vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
at the user's eye, and vertices at the top and bottom of the wall. The bottom of this triangle is the distance from the viewer to the wall. The second, similar triangle, has a point at the viewer's eye, and has a length equal to the viewer's eye from the painting. The height of the second triangle can then be determined through a simple ratio, as proven by Euclid
Euclid
Euclid , fl. 300 BC, also known as Euclid of Alexandria, was a Greek mathematician, often referred to as the "Father of Geometry". He was active in Alexandria during the reign of Ptolemy I...
. Alberti was also trained in the science of optics through the school of Padua and under the influence of Biagio Pelacani da Parma who studied Alhazen's Optics (see what was noted above in this regard with respect to Ghiberti).
Piero della Francesca
Piero della Francesca
Piero della Francesca was a painter of the Early Renaissance. As testified by Giorgio Vasari in his Lives of the Artists, to contemporaries he was also known as a mathematician and geometer. Nowadays Piero della Francesca is chiefly appreciated for his art. His painting was characterized by its...
elaborated on Della Pittura in his De Prospectiva Pingendi in the 1470s. Alberti had limited himself to figures on the ground plane and giving an overall basis for perspective. Della Francesca fleshed it out, explicitly covering solids in any area of the picture plane. Della Francesca also started the now common practice of using illustrated figures to explain the mathematical concepts, making his treatise easier to understand than Alberti's. Della Francesca was also the first to accurately draw the Platonic solids as they would appear in perspective.
Perspective remained, for a while, the domain of Florence. Jan van Eyck
Jan van Eyck
Jan van Eyck was a Flemish painter active in Bruges and considered one of the best Northern European painters of the 15th century....
, among others, was unable to create a consistent structure for the converging lines in paintings, as in London's The Arnolfini Portrait, because he was unaware of the theoretical breakthrough just then occurring in Italy. However he achieved very subtle effects by manipulations of scale in his interiors. Gradually, and partly through the movement of academies of the arts, the Italian techniques became part of the training of artists across Europe, and later other parts of the world.
Present : Computer graphics
3-D computer gamesPersonal computer game
A PC game, also known as a computer game, is a video game played on a personal computer, rather than on a video game console or arcade machine...
and ray-tracers often use a modified version of perspective. Like the painter, the computer program is generally not concerned with every ray of light that is in a scene. Instead, the program simulates rays of light traveling backwards from the monitor (one for every pixel), and checks to see what it hits. In this way, the program does not have to compute the trajectories of millions of rays of light that pass from a light source, hit an object, and miss the viewer.
CAD software, and some computer games (especially games using 3-D polygons) use linear algebra, and in particular matrix multiplication, to create a sense of perspective. The scene is a set of points, and these points are projected to a plane (computer screen) in front of the view point (the viewer's eye). The problem of perspective is simply finding the corresponding coordinates on the plane corresponding to the points in the scene. By the theories of linear algebra, a matrix multiplication directly computes the desired coordinates, thus bypassing any descriptive geometry
Descriptive geometry
Descriptive geometry is the branch of geometry which allows the representation of three-dimensional objects in two dimensions, by using a specific set of procedures. The resulting techniques are important for engineering, architecture, design and in art...
theorems used in perspective drawing.
Types of perspective
Of the many types of perspective drawings, the most common categorizations of artificial perspective are one-, two- and three-point. The names of these categories refer to the number of vanishing pointVanishing point
A vanishing point is a point in a perspective drawing to which parallel lines not parallel to the image plane appear to converge. The number and placement of the vanishing points determines which perspective technique is being used...
s in the perspective drawing.
One-point perspective

One-point perspective exists when the painting plate (also known as the picture plane
Picture plane
A picture plane is the imaginary flat surface which is usually located between the station point and the object being viewed and is ordinarily a vertical plane perpendicular to the horizontal projection of the line of sight to the object's order of interest....
) is parallel to two axes of a rectilinear (or Cartesian) scene — a scene which is composed entirely of linear elements that intersect only at right angles. If one axis is parallel with the picture plane, then all elements are either parallel to the painting plate (either horizontally or vertically) or perpendicular to it. All elements that are parallel to the painting plate are drawn as parallel lines. All elements that are perpendicular to the painting plate converge at a single point (a vanishing point) on the horizon.
Some examples:
Two-point perspective

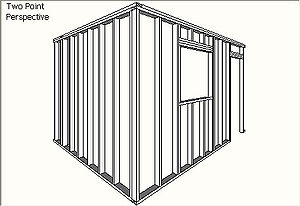
Two-point perspective exists when the painting plate is parallel to a Cartesian scene in one axis (usually the z-axis) but not to the other two axes. If the scene being viewed consists solely of a cylinder sitting on a horizontal plane, no difference exists in the image of the cylinder between a one-point and two-point perspective.
Two-point perspective has one set of lines parallel to the picture plane and two sets oblique to it. Parallel lines oblique to the picture plane converge to a vanishing point,which means that this set-up will require two vanishing points.
Three-point perspective


Three-point perspective exists when the perspective is a view of a Cartesian scene where the picture plane is not parallel to any of the scene's three axes. Each of the three vanishing points corresponds with one of the three axes of the scene. Image constructed using multiple vanishing points.
One-point, two-point, and three-point perspectives appear to embody different forms of calculated perspective. The methods required to generate these perspectives by hand are different. Mathematically, however, all three are identical: The difference is simply in the relative orientation of the rectilinear scene to the viewer.
Four-point perspective
Four-point perspective, also called infinite-point perspective, is the curvilinear variant of two-point perspective. As the result when made into an infinite point version (i.e. when the amount of vanishing points exceeds the minimum amount required), a four point perspective image becomes a panorama that can go to a 360 degree view and beyond - when going beyond the 360 degree view the artist might depict an "impossible" room as the artist might depict something new when it's supposed to show part of what already exists within those 360 degrees. This elongated frame can be used both horizontally and vertically and when used vertically can be described as an image that depicts both a worm's- and bird's-eye viewBird's-eye view
A bird's-eye view is an elevated view of an object from above, with a perspective as though the observer were a bird, often used in the making of blueprints, floor plans and maps.It can be an aerial photograph, but also a drawing...
of a scene at the same time.
As all other foreshortened variants of perspective (respectively one- to six-point perspective), it starts off with a horizon line, followed by four equally spaced vanishing points to delineate four vertical lines created in a 90 degree relation to the horizon line.
The vanishing points made to create the curvilinear orthogonals are thus made ad hoc on the four vertical lines placed on the opposite side of the horizon line. The only dimension not foreshortened in this type of perspective being the rectilinear and parallel lines at a 90 degree angle to the horizon line - similar to the vertical lines used in two-point perspective.
Zero-point perspective
Because vanishing points exist only when parallel lines are present in the scene, a perspective without any vanishing points ("zero-point" perspective) occurs if the viewer is observing a nonlinear scene. The most common example of a nonlinear scene is a natural scene (e.g., a mountain range) which frequently does not contain any parallel lines. A perspective without vanishing points can still create a sense of "depth," as is clearly apparent in a photograph of a mountain range (more distant mountains have smaller scale features).Other varieties of linear perspective
One-point, two-point, and three-point perspective are dependent on the structure of the scene being viewed. These only exist for strict Cartesian (rectilinear) scenes. By inserting into a Cartesian scene a set of parallel lines that are not parallel to any of the three axes of the scene, a new distinct vanishing point is created. Therefore, it is possible to have an infinite-point perspective if the scene being viewed is not a Cartesian scene but instead consists of infinite pairs of parallel lines, where each pair is not parallel to any other pair.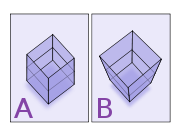
Foreshortening
Foreshortening refers to the visual effect or optical illusionOptical illusion
An optical illusion is characterized by visually perceived images that differ from objective reality. The information gathered by the eye is processed in the brain to give a perception that does not tally with a physical measurement of the stimulus source...
that an object or distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
appears shorter than it actually is because it is angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
d toward the viewer.
Although foreshortening is an important element in art
Art
Art is the product or process of deliberately arranging items in a way that influences and affects one or more of the senses, emotions, and intellect....
where visual perspective is being depicted, foreshortening occurs in other types of two-dimensional representations of three-dimensional scenes. Some other types where foreshortening can occur include oblique parallel projection
Oblique projection
Oblique projection is a simple type of graphical projection used for producing pictorial, two-dimensional images of three-dimensional objects.- Overview :Oblique projection is a type of parallel projection:...
drawings.
Figure F1 shows two different projections of a stack of two cubes, illustrating oblique parallel projection foreshortening ("A") and perspective foreshortening ("B").
Foreshortening also occurs when imaging rugged terrain using Synthetic Aperture Radar
Synthetic aperture radar
Synthetic-aperture radar is a form of radar whose defining characteristic is its use of relative motion between an antenna and its target region to provide distinctive long-term coherent-signal variations that are exploited to obtain finer spatial resolution than is possible with conventional...
systems.
This technique was often used in Renaissance painting.
Methods of construction
Several methods of constructing perspectives exist, including:- Freehand sketching (common in art)
- Graphically constructing (once common in architecture)
- Using a perspective grid
- Computing a perspective transform (common in 3D computer applications)
- Mimicry using tools such as a proportional divider (sometimes called a variscaler)
Example

To draw a square in perspective, the artist starts by drawing a horizon line (black) and determining where the vanishing point (green) should be. The higher up the horizon line is, the lower the viewer will appear to be looking, and vice versa. The more off-center the vanishing point, the more tilted the square will be. Because the square is made up of right angles, the vanishing point should be directly in the middle of the horizon line. A rotated square is drawn using two-point perspective, with each set of parallel lines leading to a different vanishing point.
The foremost edge of the (orange) square is drawn near the bottom of the painting. Because the viewer's picture plane is parallel to the bottom of the square, this line is horizontal. Lines connecting each side of the foremost edge to the vanishing point are drawn (in grey). These lines give the basic, one point "railroad tracks" perspective. The closer it is the horizon line, the farther away it is from the viewer, and the smaller it will appear. The farther away from the viewer it is, the closer it is to being perpendicular to the picture plane.
A new point (the eye) is now chosen, on the horizon line, either to the left or right of the vanishing point. The distance from this point to the vanishing point represents the distance of the viewer from the drawing. If this point is very far from the vanishing point, the square will appear squashed, and far away. If it is close, it will appear stretched out, as if it is very close to the viewer.
A line connecting this point to the opposite corner of the square is drawn. Where this (blue) line hits the side of the square, a horizontal line is drawn, representing the farthest edge of the square. The line just drawn represents the ray of light traveling from the farthest edge of the square to the viewer's eye. This step is key to understanding perspective drawing. The light that passes through the picture plane obviously can not be traced. Instead, lines that represent those rays of light are drawn on the picture plane. In the case of the square, the side of the square also represents the picture plane (at an angle), so there is a small shortcut: when the line hits the side of the square, it has also hit the appropriate spot in the picture plane. The (blue) line is drawn to the opposite edge of the foremost edge because of another shortcut: since all sides are the same length, the foremost edge can stand in for the side edge.
Original formulations used, instead of the side of the square, a vertical line to one side, representing the picture plane. Each line drawn through this plane was identical to the line of sight from the viewer's eye to the drawing, only rotated around the y-axis ninety degrees. It is, conceptually, an easier way of thinking of perspective. It can be easily shown that both methods are mathematically identical, and result in the same placement of the farthest side (see Panofsky).
Limitations
PlatoPlato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
was one of the first to discuss the problems of perspective. "Thus (through perspective) every sort of confusion is revealed within us; and this is that weakness of the human mind on which the art of conjuring and of deceiving by light and shadow and other ingenious devices imposes, having an effect upon us like magic...
And the arts of measuring and numbering and weighing come to the rescue of the human understanding—there is the beauty of them—and the apparent greater or less, or more or heavier, no longer have the mastery over us, but give way before calculation and measure and weight?"

For a typical perspective, however, the field of view is narrow enough (often only 60 degrees) that the distortions are similarly minimal enough that the image can be viewed from a point other than the actual calculated vantage point without appearing significantly distorted. When a larger angle of view is required, the standard method of projecting rays onto a flat picture plane becomes impractical. As a theoretical maximum, the field of view of a flat picture plane must be less than 180 degrees (as the field of view increases towards 180 degrees, the required breadth of the picture plane approaches infinity).
In order to create a projected ray image with a large field of view, one can project the image onto a curved surface. In order to have a large field of view horizontally in the image, a surface that is a vertical cylinder (i.e., the axis of the cylinder is parallel to the z-axis) will suffice (similarly, if the desired large field of view is only in the vertical direction of the image, a horizontal cylinder will suffice). A cylindrical picture surface will allow for a projected ray image up to a full 360 degrees in either the horizontal or vertical dimension of the perspective image (depending on the orientation of the cylinder). In the same way, by using a spherical picture surface, the field of view can be a full 360 degrees in any direction (note that for a spherical surface, all projected rays from the scene to the eye intersect the surface at a right angle).
Just as a standard perspective image must be viewed from the calculated vantage point for the image to appear identical to the true scene, a projected image onto a cylinder or sphere must likewise be viewed from the calculated vantage point for it to be precisely identical to the original scene. If an image projected onto a cylindrical surface is "unrolled" into a flat image, different types of distortions occur: For example, many of the scene's straight lines will be drawn as curves. An image projected onto a spherical surface can be flattened in various ways, including:
- an image equivalent to an unrolled cylinder
- a portion of the sphere can be flattened into an image equivalent to a standard perspective
- an image similar to a fisheye photograph
See also
- AnamorphosisAnamorphosisAnamorphosis or anamorphism may refer to any of the following:*Anamorphosis, in art, the representation of an object as seen, for instance, altered by reflection in a mirror...
- Curvilinear perspectiveCurvilinear perspectiveCurvilinear perspective is a graphical projection used to draw 3D objects on 2D surfaces. It was formally codified in 1968 by the artists and art historians André Barre and Albert Flocon in the book La Perspective curviligne, which was translated into English in 1987 as Curvilinear Perspective:...
- Cutaway drawing
- Desargues' theoremDesargues' theoremIn projective geometry, Desargues' theorem, named in honor of Gérard Desargues, states:Denote the three vertices of one triangle by a, b, and c, and those of the other by A, B, and C...
- Perspective controlPerspective controlPerspective control is a procedure for composing or editing photographs to better conform with the commonly accepted distortions in constructed perspective. The control would:...
- Perspective projection distortionPerspective projection distortionPerspective projection distortion is the inevitable misrepresentation of three-dimensional space when drawn or "projected" onto a two-dimensional surface....
- Perspective transform
- Perspective (visual)Perspective (visual)Perspective, in context of vision and visual perception, is the way in which objects appear to the eye based on their spatial attributes; or their dimensions and the position of the eye relative to the objects...
- Projective geometryProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
- Reverse perspectiveReverse perspectiveReverse perspective, also called inverse perspective, inverted perspective or Byzantine perspective, is a convention of perspective drawing where the further the objects are, the larger they are drawn. The lines diverge against the horizon, rather than converge as in linear perspective...
- ZograscopeZograscopeA zograscope is an optical device for enhancing the sense of depth perception from a flat picture. It consists of a large magnifying lens through which the picture is viewed. Some models have the lens mounted on a stand in front of an angled mirror. This allows someone to sit at a table and to look...
External links
- Teaching Perspective in Art and Mathematics through Leonardo da Vinci's Work at Convergence
- Mathematics of Perspective Drawing
- Drawing Comics - Perspective
- Quadrilateral Perspective by Yvonne Tessuto Tavares
- The Perspective Page A short interactive introduction to the geometry of perspective drawing
- Perspective Drawing Video
- The Despotic Eye: An Illustration of Metabletic Phenomenology and Its Implications by Robert D. Romanyshyn. An essay on the link between Western culture and linear perspective drawing, published in Janus Head
- Perspective in Ancient Roman-Wall Painting (c.50BC)

