
Right angle
Encyclopedia
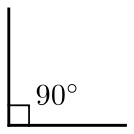
In geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and trigonometry
Trigonometry
Trigonometry is a branch of mathematics that studies triangles and the relationships between their sides and the angles between these sides. Trigonometry defines the trigonometric functions, which describe those relationships and have applicability to cyclical phenomena, such as waves...
, a right angle is an angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
that bisects the angle formed by two halves of a straight line. More precisely, if a ray is placed so that its endpoint is on a line and the adjacent angles are equal, then they are right angles. As a rotation, a right angle corresponds to a quarter turn (that is, a quarter of a full circle).
Closely related and important geometrical concepts are perpendicular
Perpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
lines, meaning lines that form right angles at their point of intersection, and orthogonality
Orthogonality
Orthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
, which is the property of forming right angles, usually applied to vectors. The presence of a right angle in a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
is the defining factor for right triangle
Right triangle
A right triangle or right-angled triangle is a triangle in which one angle is a right angle . The relation between the sides and angles of a right triangle is the basis for trigonometry.-Terminology:The side opposite the right angle is called the hypotenuse...
s, making the right angles basic to trigonometry.
The term is a calque
Calque
In linguistics, a calque or loan translation is a word or phrase borrowed from another language by literal, word-for-word or root-for-root translation.-Calque:...
of Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
angulus rectus; here rectus means "upright", referring to the vertical perpendicular to a horizontal base line.
Symbols
In UnicodeUnicode
Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...
, the symbol for a right angle is . Variations are and and .
In diagrams the fact that an angle is a right angle is usually expressed by adding small right angle that forms a square with the angle in the diagram, as seen the diagram of a right triangle to the right. Other variants include having a curved angle, but with a small dot in the angle field.
Euclid
Right angles are fundamental in Euclid's ElementsEuclid's Elements
Euclid's Elements is a mathematical and geometric treatise consisting of 13 books written by the Greek mathematician Euclid in Alexandria c. 300 BC. It is a collection of definitions, postulates , propositions , and mathematical proofs of the propositions...
. They are defined in Book 1, definition 10, which also defines perpendicular lines. Euclid uses right angles in definitions 11 and 12 to define acute angles (those smaller than a right angle) and obtuse angles (those greater than a right angle). Two angles are called complementary
Complementary angles
In geometry, complementary angles are angles whose measures sum to 90°. If the two complementary angles are adjacent their non-shared sides form a right angle....
if their sum is a right angle.
Book 1 Postulate 4 states that all right angles are equal, which allows Euclid to use a right angle as a unit to measure other angles with. Euclid's commentator Proclus
Proclus
Proclus Lycaeus , called "The Successor" or "Diadochos" , was a Greek Neoplatonist philosopher, one of the last major Classical philosophers . He set forth one of the most elaborate and fully developed systems of Neoplatonism...
gave a proof of this postulate using the previous postulates, but it may be argued that this proof makes use of some hidden assumptions. Saccheri
Giovanni Girolamo Saccheri
Giovanni Girolamo Saccheri was an Italian Jesuit priest, scholastic philosopher, and mathematician....
gave a proof as well but using a more explicit assumption. In Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
's axiomatization of geometry
Hilbert's axioms
Hilbert's axioms are a set of 20 assumptions proposed by David Hilbert in 1899 in his book Grundlagen der Geometrie , as the foundation for a modern treatment of Euclidean geometry...
this statement is given as a theorem, but only after much groundwork. One may argue that, even if postulate 4 can be proven from the preceding ones, in the order that Euclid presents his material it is necessary to include it since without it postulate 5, which uses the right angle as a unit of measure, makes no sense.
Conversion to other units
A right angle may be expressed in different units:- 1/4 turnTurn (geometry)A turn is an angle equal to a 360° or 2 radians or \tau radians. A turn is also referred to as a revolution or complete rotation or full circle or cycle or rev or rot....
. - 90° (degreesDegree (angle)A degree , usually denoted by ° , is a measurement of plane angle, representing 1⁄360 of a full rotation; one degree is equivalent to π/180 radians...
) - π/2 radianRadianRadian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s - 100 gradGrad (angle)The gradian is a unit of plane angle, equivalent to of a turn. It is also known as gon, grad, or grade . One grad equals of a degree or of a radian...
(also called grade, gradian, or gon) - 8 points (of a 32-point compass roseCompass roseA compass rose, sometimes called a windrose, is a figure on a compass, map, nautical chart or monument used to display the orientation of the cardinal directions — North, East, South and West - and their intermediate points. It is also the term for the graduated markings found on the traditional...
) - 6 hours (astronomical hour angleHour angleIn astronomy and celestial navigation, the hour angle is one of the coordinates used in the equatorial coordinate system to give the position of a point on the celestial sphere....
)
Rule of 3-4-5
Throughout history carpenters and masons have known a quick way to confirm if an angle is a true "right angle." It is based on the most widely known Pythagorean triplePythagorean triple
A Pythagorean triple consists of three positive integers a, b, and c, such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer k. A primitive Pythagorean triple is one in which a, b and c are pairwise coprime...
(3, 4, 5) and so called the "Rule of 3-4-5." From the angle in question, running a straight line along one side exactly three units in length, and along the second side exactly four units in length, will create a hypotenuse
Hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse of a right triangle can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equals the sum of the squares of the...
(the longer line opposite the right angle that connects the two measured endpoints) of exactly 5 units in length. This measurement can be made quickly and without technical instruments. The geometric law behind the measurement is the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
("The square of the hypotenuse of a right triangle is equal to the sum of the squares of the two adjacent sides").
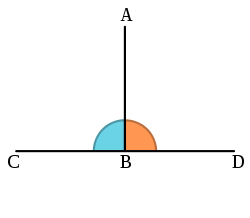
Thales' theorem
Thales' theorem states that an angle inscribed in a semicircle is a right angle.See also
- Cartesian coordinate systemCartesian coordinate systemA Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
- OrthogonalityOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
- PerpendicularPerpendicularIn geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
- RectangleRectangleIn Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
- Types of angles

