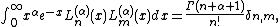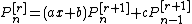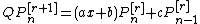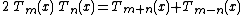Orthogonal polynomials
Encyclopedia
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials
, and consist of the Hermite polynomials
, the Laguerre polynomials
, the Jacobi polynomials
together with their special cases the ultraspherical polynomials, the Chebyshev polynomials
, and the Legendre polynomials.
They have many important applications in such areas as mathematical physics (in particular, the theory of random matrices), approximation theory
, numerical analysis
, and many others.
Classical orthogonal polynomials appeared in the early 19th century in the works of Adrien-Marie Legendre
, who introduced the Legendre polynomials. In the late 19th century, the study of continued fraction
s by P. L. Chebyshev
and then A.A. Markov
and T.J. Stieltjes
led to the general notion of orthogonal polynomials.
The classical orthogonal polynomials are characterized by being solutions to a differential equation of the form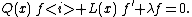
There are several more general definitions of orthogonal classical polynomials; for example, use the term for all polynomials in the Askey scheme
.
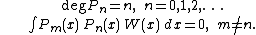
The relations above define Pn up to multiplication by a number. Various normalisations are used to fix the constant, e.g.
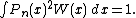
The classical orthogonal polynomials correspond to the three families of weights:
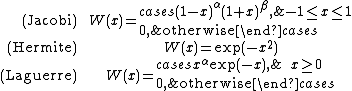
The standard normalisation (also called standartisation) is detailed below.

They are normalised (standartised) by
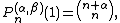
and satisfy the orthogonality condition
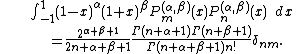
The Jacobi polynomials are solutions to the differential equation
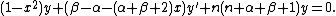
(with parameter γ = α + ½).
For α = β = 0, these are called the Legendre polynomials (for which the interval of orthogonality is [−1, 1] and the weight function is simply 1):
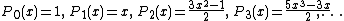
For α = β = ±½, one obtains the Chebyshev polynomials
(of the second and first kind, respectively).
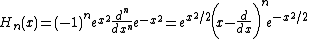
They satisfy the orthogonality condition
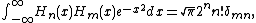
and the differential equation
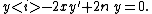
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
, and consist of the Hermite polynomials
Hermite polynomials
In mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
, the Laguerre polynomials
Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
, the Jacobi polynomials
Jacobi polynomials
In mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
together with their special cases the ultraspherical polynomials, the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
, and the Legendre polynomials.
They have many important applications in such areas as mathematical physics (in particular, the theory of random matrices), approximation theory
Approximation theory
In mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
, numerical analysis
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
, and many others.
Classical orthogonal polynomials appeared in the early 19th century in the works of Adrien-Marie Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
, who introduced the Legendre polynomials. In the late 19th century, the study of continued fraction
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
s by P. L. Chebyshev
Pafnuty Chebyshev
Pafnuty Lvovich Chebyshev was a Russian mathematician. His name can be alternatively transliterated as Chebychev, Chebysheff, Chebyshov, Tschebyshev, Tchebycheff, or Tschebyscheff .-Early years:One of nine children, Chebyshev was born in the village of Okatovo in the district of Borovsk,...
and then A.A. Markov
Andrey Markov
Andrey Andreyevich Markov was a Russian mathematician. He is best known for his work on theory of stochastic processes...
and T.J. Stieltjes
Thomas Joannes Stieltjes
Thomas Joannes Stieltjes was a Dutch mathematician. He was born in Zwolle and died in Toulouse, France. He was a pioneer in the field of moment problems and contributed to the study of continued fractions....
led to the general notion of orthogonal polynomials.
The classical orthogonal polynomials are characterized by being solutions to a differential equation of the form
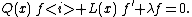
There are several more general definitions of orthogonal classical polynomials; for example, use the term for all polynomials in the Askey scheme
Askey scheme
In mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in , the Askey scheme was first drawn by and by , and has since been extended by and to cover basic...
.
Definition
In general, the orthogonal polynomials Pn with respect to a weight W:R→R+ on the real line are defined by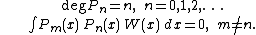
The relations above define Pn up to multiplication by a number. Various normalisations are used to fix the constant, e.g.
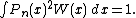
The classical orthogonal polynomials correspond to the three families of weights:
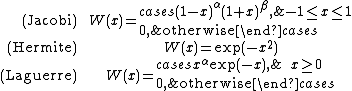
The standard normalisation (also called standartisation) is detailed below.
Jacobi polynomials
For α,β > −1 the Jacobi polynomials are given by the formula
They are normalised (standartised) by
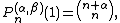
and satisfy the orthogonality condition
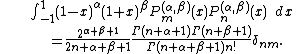
The Jacobi polynomials are solutions to the differential equation
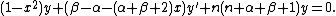
Important special cases
The Jacobi polynomials with α = β are called the Gegenbauer polynomialsGegenbauer polynomials
In mathematics, Gegenbauer polynomials or ultraspherical polynomials C are orthogonal polynomials on the interval [−1,1] with respect to the weight function α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials...
(with parameter γ = α + ½).
For α = β = 0, these are called the Legendre polynomials (for which the interval of orthogonality is [−1, 1] and the weight function is simply 1):
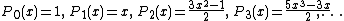
For α = β = ±½, one obtains the Chebyshev polynomials
Chebyshev polynomials
In mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
(of the second and first kind, respectively).
Hermite polynomials
The Hermite polynomials are defined by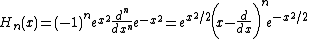
They satisfy the orthogonality condition
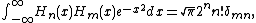
and the differential equation
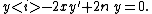
Laguerre polynomials
The generalised Laguerre polynomials are defined by-
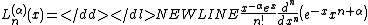
(the classical Laguerre polynomials correspond to α=0.)
They satisfy the orthogonality relation
and the differential equation
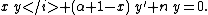
Differential equation
The classical orthogonal polynomials arise from a differential equation of the form

where Q is a given quadratic (at most) polynomial, and L is a given linear polynomial. The function f, and the constant λ, are to be found.
This is a Sturm-Liouville type of equation. Such equations generally have singularities in their solution functions f except for particular values of λ. They can be thought of an eigenvector/eigenvalue problems: Letting D be the differential operatorDifferential operatorIn mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, , and changing the sign of λ, the problem is to find the eigenvectors (eigenfunctions) f, and the
, and changing the sign of λ, the problem is to find the eigenvectors (eigenfunctions) f, and the
corresponding eigenvalues λ, such that f does not have singularities and D(f) = λf.
The solutions of this differential equation have singularities unless λ takes on
specific values. There is a series of numbers that lead to a series of polynomial solutions
that lead to a series of polynomial solutions 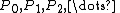 if one of the following sets of conditions are met:
if one of the following sets of conditions are met:
- Q is actually quadratic, L is linear, Q has two distinct real roots, the root of L lies strictly between the roots of Q, and the leading terms of Q and L have the same sign.
- Q is not actually quadratic, but is linear, L is linear, the roots of Q and L are different, and the leading terms of Q and L have the same sign if the root of L is less than the root of Q, or vice-versa.
- Q is just a nonzero constant, L is linear, and the leading term of L has the opposite sign of Q.
These three cases lead to the Jacobi-like, Laguerre-like, and Hermite-like polynomials, respectively.
In each of these three cases, we have the following:
- The solutions are a series of polynomials
 , each
, each  having degree n, and corresponding to a number
having degree n, and corresponding to a number 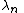 .
. - The interval of orthogonality is bounded by whatever roots Q has.
- The root of L is inside the interval of orthogonality.
- Letting
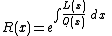 , the polynomials are orthogonal under the weight function
, the polynomials are orthogonal under the weight function 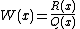
- W(x) has no zeros or infinities inside the interval, though it may have zeros or infinities at the end points.
- W(x) gives a finite inner product to any polynomials.
- W(x) can be made to be greater than 0 in the interval. (Negate the entire differential equation if necessary so that Q(x) > 0 inside the interval.)
Because of the constant of integration, the quantity R(x) is determined only up to an arbitrary positive multiplicative constant. It will be used only in homogeneous differential equations
(where this doesn't matter) and in the definition of the weight function (which can also be
indeterminate.) The tables below will give the "official" values of R(x) and W(x).
Rodrigues' formula
Under the assumptions of the preceding section,
Pn(x) is proportional to
This is known as Rodrigues' formulaRodrigues' formulaIn mathematics, Rodrigues's formula is a formula for Legendre polynomials independently introduced by , and...
, after Olinde RodriguesOlinde RodriguesBenjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
. It is often written
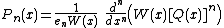
where the numbers en depend on the standardization. The standard values of en will be given in the tables below.
The numbers λn
Under the assumptions of the preceding section, we have
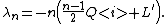
(Since Q is quadratic and L is linear,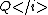 and
and 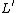 are constants, so these are just numbers.)
are constants, so these are just numbers.)
Second form for the differential equation
Let
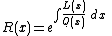 .
.
Then
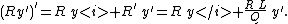
Now multiply the differential equation
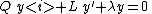
by R/Q, getting
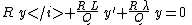
or

This is the standard Sturm-Liouville form for the equation.
Third form for the differential equation
Let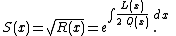
Then

Now multiply the differential equation
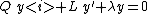
by S/Q, getting
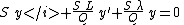
or

But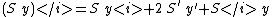 , so
, so
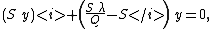
or, letting u = Sy,

Formulas involving derivatives
Under the assumptions of the preceding section, let denote the rth derivative of
denote the rth derivative of 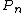 .
.
(We put the "r" in brackets to avoid confusion with an exponent.)
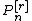 is a polynomial of degree n − r. Then we have the following:
is a polynomial of degree n − r. Then we have the following:
- (orthogonality) For fixed r, the polynomial sequence
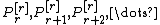 are orthogonal, weighted by
are orthogonal, weighted by 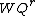 .
. - (generalized Rodrigues'Olinde RodriguesBenjamin Olinde Rodrigues , more commonly known as Olinde Rodrigues, was a French banker, mathematician, and social reformer.Rodrigues was born into a well-to-do Sephardi Jewish family in Bordeaux....
formula) is proportional to
is proportional to 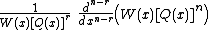 .
. - (differential equation)
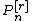 is a solution of
is a solution of 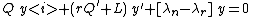 , where
, where 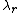 is the same function as
is the same function as 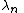 , that is,
, that is, 
- (differential equation, second form)
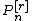 is a solution of
is a solution of 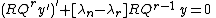
There are also some mixed recurrences. In each of these, the numbers a, b, and c depend on n
and r, and are unrelated in the various formulas.
There are an enormous number of other formulas involving orthogonal polynomials
in various ways. Here is a tiny sample of them, relating to the Chebyshev,
associated Laguerre, and Hermite polynomials:
Orthogonality
The differential equation for a particular λ may be written (omitting explicit dependence on x)
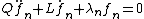
multiplying by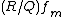 yields
yields

and reversing the subscripts yields
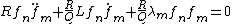
subtracting and integrating:
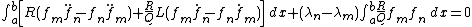
but it can be seen that
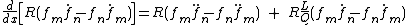
so that:
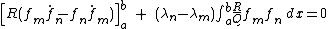
If the polynomials f are such that the term on the left is zero, and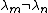 for
for  , then the orthogonality relationship will hold:
, then the orthogonality relationship will hold:
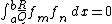
for .
.
Derivation from differential equation
All of the polynomial sequences arising from the differential equation above are equivalent, under scaling and/or shifting of the domain, and standardizing of the polynomials, to more restricted classes. Those restricted classes are exactly "classical orthogonal polynomials".
- Every Jacobi-like polynomial sequence can have its domain shifted and/or scaled so that its interval of orthogonality is [−1, 1], and has Q = 1 − x2. They can then be standardized into the Jacobi polynomials
 . There are several important subclasses of these: Gegenbauer, Legendre, and two types of Chebyshev.
. There are several important subclasses of these: Gegenbauer, Legendre, and two types of Chebyshev. - Every Laguerre-like polynomial sequence can have its domain shifted, scaled, and/or reflected so that its interval of orthogonality is
 , and has Q = x. They can then be standardized into the Associated Laguerre polynomials
, and has Q = x. They can then be standardized into the Associated Laguerre polynomials  . The plain Laguerre polynomials
. The plain Laguerre polynomials 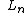 are a subclass of these.
are a subclass of these. - Every Hermite-like polynomial sequence can have its domain shifted and/or scaled so that its interval of orthogonality is
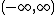 , and has Q = 1 and L(0) = 0. They can then be standardized into the Hermite polynomials
, and has Q = 1 and L(0) = 0. They can then be standardized into the Hermite polynomials 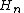 .
.
Because all polynomial sequences arising from a differential equation in the manner
described above are trivially equivalent to the classical polynomials, the actual classical
polynomials are always used.
Jacobi polynomial
The Jacobi-like polynomials, once they have had their domain shifted and scaled so that
the interval of orthogonality is [−1, 1], still have two parameters to be determined.
They are and
and 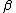 in the Jacobi polynomials,
in the Jacobi polynomials,
written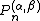 . We have
. We have 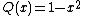 and
and
 .
.
Both and
and 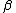 are required to be greater than −1.
are required to be greater than −1.
(This puts the root of L inside the interval of orthogonality.)
When and
and 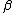 are not equal, these polynomials
are not equal, these polynomials
are not symmetrical about x = 0.
The differential equation
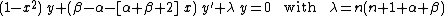
is Jacobi's equation.
For further details, see Jacobi polynomialsJacobi polynomialsIn mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
.
Gegenbauer polynomials
When one sets the parameters and
and 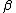
in the Jacobi polynomials equal to each other, one obtains the
Gegenbauer or ultraspherical polynomials. They are
written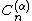 , and defined as
, and defined as
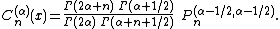
We have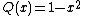 and
and
 .
.
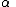 is required to be greater than −1/2.
is required to be greater than −1/2.
(Incidentally, the standardization given in the table below would make no sense for α = 0 and n ≠ 0, because it would set the polynomials to zero. In that case, the accepted standardization sets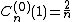 instead of the value given in the table.)
instead of the value given in the table.)
Ignoring the above considerations, the parameter is closely related to the derivatives of
is closely related to the derivatives of  :
:
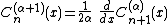
or, more generally:
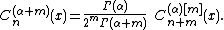
All the other classical Jacobi-like polynomials (Legendre, etc.) are
special cases of the Gegenbauer polynomials, obtained by choosing a value of
and choosing a standardization.
For further details, see Gegenbauer polynomialsGegenbauer polynomialsIn mathematics, Gegenbauer polynomials or ultraspherical polynomials C are orthogonal polynomials on the interval [−1,1] with respect to the weight function α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials...
.
Legendre polynomials
The differential equation is
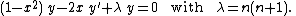
This is Legendre's equation.
The second form of the differential equation is:
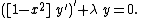
The recurrence relation is

A mixed recurrence is
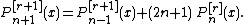
Rodrigues' formula is

For further details, see Legendre polynomials.
Associated Legendre polynomials
The Associated Legendre polynomialsAssociated Legendre polynomialsIn mathematics, the associated Legendre polynomials are the canonical solutions of the general Legendre equation\,y -2xy' + \left\,y = 0,\,or equivalently...
, denoted
 where
where 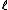 and
and 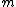 are integers with
are integers with  , are defined as
, are defined as
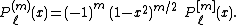
The m in parentheses (to avoid confusion with an exponent) is a parameter. The m
in brackets denotes the mth derivative of the Legendre polynomial.
These "polynomials" are misnamed—they are not polynomials when m is odd.
They have a recurrence relation:
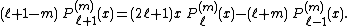
For fixed m, the sequence are orthogonal over [−1, 1], with weight 1.
are orthogonal over [−1, 1], with weight 1.
For given m,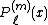 are the solutions of
are the solutions of
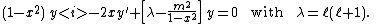
Chebyshev polynomials
The differential equation is
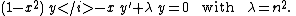
This is Chebyshev's equation.
The recurrence relation is

Rodrigues' formula is

These polynomials have the property that, in the interval of orthogonality,
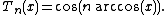
(To prove it, use the recurrence formula.)
This means that all their local minima and maxima have values of −1 and +1,
that is, the polynomials are "level". Because of this, expansion of functions
in terms of Chebyshev polynomials is sometimes used for polynomial
approximationsApproximation theoryIn mathematics, approximation theory is concerned with how functions can best be approximated with simpler functions, and with quantitatively characterizing the errors introduced thereby...
in computer math libraries.
Some authors use versions of these polynomials that have been shifted so that the
interval of orthogonality is [0, 1] or [−2, 2].
There are also Chebyshev polynomials of the second kind, denoted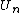
We have:
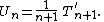
For further details, including the expressions for the first few
polynomials, see Chebyshev polynomialsChebyshev polynomialsIn mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
.
Laguerre polynomials
The most general Laguerre-like polynomials, after the domain has been shifted
and scaled, are the Associated Laguerre polynomials (also called Generalized Laguerre polynomials),
denoted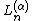 . There is a parameter
. There is a parameter  , which can be any
, which can be any
real number strictly greater than −1. The parameter is put in parentheses to avoid confusion
with an exponent. The plain Laguerre polynomials are simply the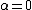
version of these:
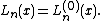
The differential equation is
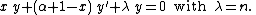
This is Laguerre's equation.
The second form of the differential equation is
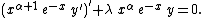
The recurrence relation is
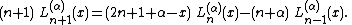
Rodrigues' formula is
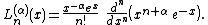
The parameter is closely related to the derivatives of
is closely related to the derivatives of 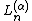 :
:
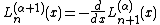
or, more generally:
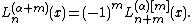
Laguerre's equation can be manipulated into a form that is more useful in applications:

is a solution of

This can be further manipulated. When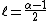 is an integer, and
is an integer, and 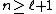 :
:
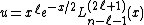
is a solution of

The solution is often expressed in terms of derivatives instead of associated Laguerre polynomials:
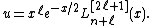
This equation arises in quantum mechanics, in the radial part of the solution
of the Schrödinger equationSchrödinger equationThe Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a one-electron atom.
Physicists often use a definition for the Laguerre polynomials that is larger,
by a factor of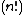 , than the definition used here.
, than the definition used here.
For further details, including the expressions for the first few polynomials, see Laguerre polynomialsLaguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
.
Hermite polynomials
The differential equation is

This is Hermite's equation.
The second form of the differential equation is
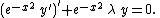
The third form is
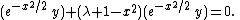
The recurrence relation is

Rodrigues' formula is

The first few Hermite polynomials are
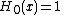

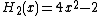
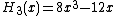
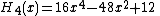
One can define the associated Hermite functions
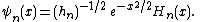
Because the multiplier is proportional to the square root of the weight function, these functions
are orthogonal over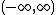 with no weight function.
with no weight function.
The third form of the differential equation above, for the associated Hermite functions, is

The associated Hermite functions arise in many areas of mathematics and physics.
In quantum mechanics, they are the solutions of Schrödinger's equation for the harmonic oscillator.
They are also eigenfunctions (with eigenvalue (−i)n) of the continuous Fourier transformContinuous Fourier transformThe Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
.
Many authors, particularly probabilists, use an alternate definition of the Hermite polynomials, with a weight function of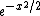 instead of
instead of 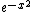 . If the notation He is used for these Hermite polynomials, and H for those above, then these may be characterized by
. If the notation He is used for these Hermite polynomials, and H for those above, then these may be characterized by
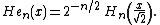
For further details, see Hermite polynomialsHermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
.
Characterizations of classical orthogonal polynomials
There are several conditions that single out the classical orthogonal polynomials from the others.
The first condition was found by Sonine (and later by Hahn), who showed that (up to linear changes of variable) the classical orthogonal polynomials are the only ones such that their derivatives are also orthogonal polynomials.
Bochner characterized classical orthogonal polynomials in terms of their recurrence relations.
Tricomi characterized classical orthogonal polynmials as those that have a certain analogue of the Rodrigues formula.
Table of classical orthogonal polynomials
The following table summarises the properties of the classical orthogonal polynomials.
Name, and conventional symbol Chebyshev Chebyshev polynomialsIn mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
,
Chebyshev Chebyshev polynomialsIn mathematics the Chebyshev polynomials, named after Pafnuty Chebyshev, are a sequence of orthogonal polynomials which are related to de Moivre's formula and which can be defined recursively. One usually distinguishes between Chebyshev polynomials of the first kind which are denoted Tn and...
(second kind),
Legendre, 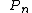
Hermite Hermite polynomialsIn mathematics, the Hermite polynomials are a classical orthogonal polynomial sequence that arise in probability, such as the Edgeworth series; in combinatorics, as an example of an Appell sequence, obeying the umbral calculus; in numerical analysis as Gaussian quadrature; and in physics, where...
,
Limits of orthogonality 
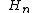
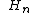

Weight, 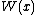

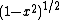

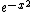
Standardization 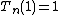
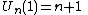
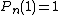
Lead term = 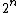
Square of norm 
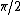


Leading term 



Second term, 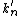

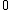
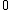

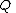
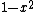

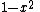
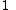
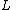
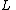
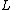

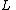
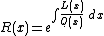
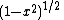
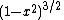
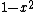
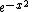
Constant in diff. equation, 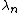
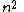
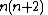
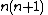

Constant in Rodrigues' formula, 
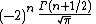

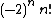

Recurrence relation, 
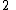
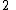
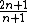

Recurrence relation, 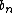
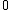
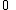


Recurrence relation, 
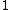

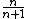
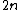
Name, and conventional symbol Associated Laguerre Laguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
,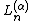
Laguerre Laguerre polynomialsIn mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
,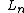
Limits of orthogonality 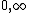

Weight, 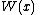
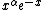

Standardization Lead term = 
Lead term = 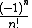
Square of norm, 
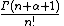
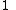
Leading term, 

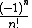
Second term, 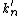
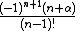

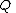
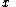

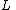
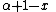
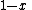
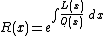
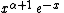
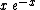
Constant in diff. equation, 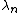
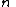
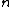
Constant in Rodrigues' formula, 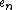
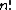
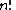
Recurrence relation, 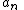
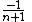

Recurrence relation, 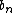


Recurrence relation, 
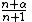
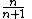
Name, and conventional symbol Gegenbauer Gegenbauer polynomialsIn mathematics, Gegenbauer polynomials or ultraspherical polynomials C are orthogonal polynomials on the interval [−1,1] with respect to the weight function α–1/2. They generalize Legendre polynomials and Chebyshev polynomials, and are special cases of Jacobi polynomials...
,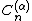
Jacobi Jacobi polynomialsIn mathematics, Jacobi polynomials are a class of classical orthogonal polynomials. They are orthogonal with respect to the weight ^\alpha ^\beta on the interval [-1, 1]...
,
Limits of orthogonality 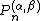
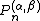
Weight, 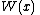
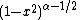
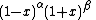
Standardization 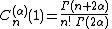 if
if 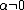
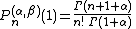
Square of norm, 
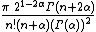
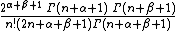
Leading term, 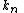
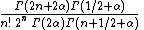
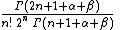
Second term, 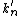
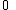
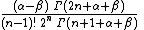
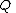
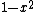



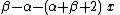

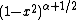

Constant in diff. equation, 
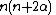
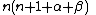
Constant in Rodrigues' formula, 
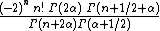
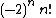
Recurrence relation, 
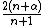
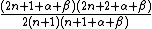
Recurrence relation, 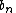
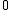

Recurrence relation, 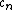
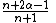

See also
- Appell sequence
- Askey schemeAskey schemeIn mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in , the Askey scheme was first drawn by and by , and has since been extended by and to cover basic...
of hypergeometric orthogonal polynomials - Polynomial sequences of binomial type
- Biorthogonal polynomials
- Generalized Fourier seriesGeneralized Fourier seriesIn mathematical analysis, many generalizations of Fourier series have proved to be useful.They are all special cases of decompositions over an orthonormal basis of an inner product space....
- Secondary measureSecondary measureIn mathematics, the secondary measure associated with a measure of positive density \rho when there is one, is a measure of positive density \mu, turning the secondary polynomials associated with the orthogonal polynomials for \rho into an orthogonal system....
- Sheffer sequence
- Umbral calculusUmbral calculusIn mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
-