
Naive set theory
Encyclopedia
Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics
. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics
(for example Venn diagram
s and symbolic reasoning about their Boolean algebra), and the everyday usage of set theory concepts in most contemporary mathematics.
Sets are of great importance in mathematics
; in fact, in modern formal treatments, most mathematical objects (number
s, relations
, functions
, etc.) are defined in terms of sets. Naive set theory can be seen as a stepping-stone to more formal treatments, and suffices for many purposes.
to describe sets. The words and, or, if ... then, not, for some, for every are not subject to rigorous definition. It is useful to study sets naively at an early stage of mathematics in order to develop facility for working with them. Furthermore, a firm grasp of set theoretical concepts from a naive standpoint is important as a first stage in understanding the motivation for the formal axioms of set theory.
This article develops a naive theory. Sets are defined informally and a few of their properties are investigated. Links in this article to specific axioms of set theory describe some of the relationships between the informal discussion here and the formal axiomatization of set theory, but no attempt is made to justify every statement on such a basis. The first development of set theory
was a naive set theory. It was created at the end of the 19th century by Georg Cantor
as part of his study of infinite sets.
As it turned out, assuming that one can perform any operation on sets without restriction leads to paradox
es such as Russell's paradox
and Berry's paradox. Some believe that Georg Cantor
's set theory was not actually implicated by these paradox
es (see Frápolli 1991); one difficulty in determining this with certainty is that Cantor did not provide an axiomatization of his system. It is undisputed that, by 1900, Cantor was aware of some of the paradoxes and did not believe that they discredited his theory. Gottlob Frege
did explicitly axiomatize a theory in which the formalized version of naive set theory can be interpreted, and it is this formal theory which Bertrand Russell
actually addressed when he presented his paradox.
Axiomatic set theory was developed in response to these early attempts to study set theory, with the goal of determining precisely what operations were allowed and when. Today, when mathematicians talk about "set theory" as a field, they usually mean axiomatic set theory. Informal applications of set theory in other fields are sometimes referred to as applications of "naive set theory", but usually are understood to be justifiable in terms of an axiomatic system
(normally the Zermelo–Fraenkel set theory
).
A naive set theory is not necessarily inconsistent, if it correctly specifies the sets allowed to be considered. This can be done by the means of definitions, which are implicit axioms. It can be done by systematically making explicit all the axioms, as in the case of the well-known book Naive Set Theory by Paul Halmos
, which is actually a somewhat (not all that) informal presentation of the usual axiomatic Zermelo–Fraenkel set theory
. It is 'naive' in that the language and notations are those of ordinary informal mathematics, and in that it doesn't deal with consistency or completeness of the axiom system. However, the term naive set theory is also used in some literature to refer to the set theories studied by Frege and Cantor, rather than to the informal counterparts of modern axiomatic set theory; care is required to tell which sense is intended.
s. Clearly, the set of even numbers is infinitely large; there is no requirement that a set be finite.
If x is a member of A, then it is also said that x belongs to A, or that x is in A. In this case, we write x ∈ A.
(The symbol ∈ is a derivation from the Greek letter
epsilon
, "ε", introduced by Peano in 1888.)
The symbol ∉ is sometimes used to write x ∉ A, meaning "x is not in A".
Two sets A and B are defined to be equal when they have precisely the same elements, that is, if every element of A is an element of B and every element of B is an element of A. (See axiom of extensionality
.) Thus a set is completely determined by its elements; the description is immaterial. For example, the set with elements 2, 3, and 5 is equal to the set of all prime number
s less than 6.
If the sets A and B are equal, this is denoted symbolically as A = B (as usual).
We also allow for an empty set
, often denoted Ø and sometimes : a set without any members at all.
Since a set is determined completely by its elements, there can only be one empty set. (See axiom of empty set
.) Note that Ø ≠ {Ø}.
(See axiom of pairing
.)
Note the following points:
(These are consequences of the definition of equality in the previous section.)
This notation can be informally abused by saying something like {dogs} to indicate the set of all dogs, but this example would usually be read by mathematicians as "the set containing the single element dogs".
An extreme (but correct) example of this notation is {}, which denotes the empty set.
We can also use the notation {x : P(x)}, or sometimes {x | P(x)}, to denote the set containing all objects for which the condition P holds (known as defining a set intensionally).
For example, {x : x is a real number} denotes the set of real number
s, {x : x has blonde hair} denotes the set of everything with blonde hair, and {x : x is a dog} denotes the set of all dogs.
This notation is called set-builder notation
(or "set comprehension", particularly in the context of Functional programming
).
Some variants of set builder notation are:
of B if every element of A is also an element of B.
Notice that in particular, B is a subset of itself; a subset of B that isn't equal to B is called a proper subset.
If A is a subset of B, then one can also say that B is a superset of A, that A is contained in B, or that B contains A.
In symbols, A ⊆ B means that A is a subset of B, and B ⊇ A means that B is a superset of A.
Some authors use the symbols "⊂" and "⊃" for subsets, and others use these symbols only for proper subsets. For clarity, one can explicitly use the symbols "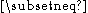 " and "
" and "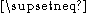 " to indicate non-equality.
" to indicate non-equality.
As an illustration, let R be the set of real numbers, let Z be the set of integers, let O be the set of odd integers, and let P be the set of current or former U.S. Presidents
.
Then O is a subset of Z, Z is a subset of R, and (hence) O is a subset of R, where in all cases subset may even be read as proper subset.
Note that not all sets are comparable in this way.
For example, it is not the case either that R is a subset of P nor that P is a subset of R.
It follows immediately from the definition of equality of sets above that, given two sets A and B, A = B if and only if A ⊆ B and B ⊆ A. In fact this is often given as the definition of equality. Usually when trying to prove
that two sets are equal, one aims to show these two inclusions. Note that the empty set
is a subset of every set (the statement that all elements of the empty set are also members of any set A is vacuously true).
The set of all subsets of a given set A is called the power set of A and is denoted by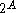 or
or 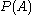 ; the "P" is sometimes in a fancy font. If the set A has n elements, then
; the "P" is sometimes in a fancy font. If the set A has n elements, then 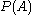 will have
will have  elements.
elements.
.
For instance, if we are investigating properties of the real number
s R (and subsets of R), then we may take R as our universal set. A universal set is only temporarily defined by the context; there is no such thing as a "universal" universal set, "the set of everything" (see Paradoxes below).
Given a universal set U and a subset A of U, we may define the complement
of A (in U) as
In other words, AC ("A-complement"; sometimes simply A, "A-prime" ) is the set of all members of U which are not members of A.
Thus with R, Z and O defined as in the section on subsets, if Z is the universal set, then OC is the set of even integers, while if R is the universal set, then OC is the set of all real numbers that are either even integers or not integers at all.
.
This is the set consisting of all objects which are elements of A or of B or of both (see axiom of union
). It is denoted by A ∪ B.
The intersection
of A and B is the set of all objects which are both in A and in B. It is denoted by A ∩ B.
Finally, the relative complement
of B relative to A, also known as the set theoretic difference of A and B, is the set of all objects that belong to A but not to B. It is written as A \ B or A − B.
Symbolically, these are respectively
Notice that A doesn't have to be a subset of B for B \ A to make sense; this is the difference between the relative complement and the absolute complement from the previous section.
To illustrate these ideas, let A be the set of left-handed people, and let B be the set of people with blond hair.
Then A ∩ B is the set of all left-handed blond-haired people, while A ∪ B is the set of all people who are left-handed or blond-haired or both.
A \ B, on the other hand, is the set of all people that are left-handed but not blond-haired, while B \ A is the set of all people who have blond hair but aren't left-handed.
Now let E be the set of all human beings, and let F be the set of all living things over 1000 years old.
What is E ∩ F in this case?
No living human being is over 1000 years old
, so E ∩ F must be the empty set
{}.
For any set A, the power set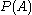 is a Boolean algebra under the operations of union and intersection.
is a Boolean algebra under the operations of union and intersection.
is simply a collection of two objects such that one can be distinguished as the first element and the other as the second element, and having the fundamental property that, two ordered pairs are equal if and only if their first elements are equal and their second elements are equal.
Formally, an ordered pair with first coordinate a, and second coordinate b, usually denoted by (a, b), can be defined as the set .
It follows that, two ordered pairs (a,b) and (c,d) are equal if and only if a = c and b = d.
Alternatively, an ordered pair can be formally thought of as a set {a,b} with a total order
.
(The notation (a, b) is also used to denote an open interval on the real number line, but the context should make it clear which meaning is intended. Otherwise, the notation ]a, b[ may be used to denote the open interval whereas (a, b) is used for the ordered pair).
If A and B are sets, then the Cartesian product
(or simply product) is defined to be:
That is, A × B is the set of all ordered pairs whose first coordinate is an element of A and whose second coordinate is an element of B.
We can extend this definition to a set A × B × C of ordered triples, and more generally to sets of ordered n-tuples for any positive integer n.
It is even possible to define infinite Cartesian product
s, but to do this we need a more recondite definition of the product.
Cartesian products were first developed by René Descartes
in the context of analytic geometry
.
If R denotes the set of all real number
s, then R2 := R × R represents the Euclidean plane and R3 := R × R × R represents three-dimensional Euclidean space
.
s, and r and s are real number
s.
Now for the problem: is Z a member of Z? If yes, then by the defining quality of Z, Z is not a member of itself, i.e., Z is not a member of Z. This forces us to declare that Z is not a member of Z. Then Z is not a member of itself and so, again by definition of Z, Z is a member of Z.
Thus both options lead us to a contradiction and we have an inconsistent theory. More succinctly, one says that Z is a member of Z if and only if Z is not a member of Z. Axiomatic developments place restrictions on the sort of sets we are allowed to form and thus prevent problems like our set Z from arising. This particular paradox is Russell's paradox
.
The penalty is that one must take more care with one's development, as one must in any rigorous mathematical argument.
In particular, it is problematic to speak of a set of everything, or to be (possibly) a bit less ambitious, even a set of all sets.
In fact, in the standard axiomatisation of set theory, there is no set of all sets.
In areas of mathematics that seem to require a set of all sets (such as category theory
), one can sometimes make do with a universal set so large that all of ordinary mathematics can be done within it (see universe
).
Alternatively, one can make use of proper classes
.
Or, one can use a different axiomatisation of set theory, such as W. V. Quine's New Foundations
, which allows for a set of all sets and avoids Russell's paradox in another way.
Foundations of mathematics
Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...
. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics
Discrete mathematics
Discrete mathematics is the study of mathematical structures that are fundamentally discrete rather than continuous. In contrast to real numbers that have the property of varying "smoothly", the objects studied in discrete mathematics – such as integers, graphs, and statements in logic – do not...
(for example Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s and symbolic reasoning about their Boolean algebra), and the everyday usage of set theory concepts in most contemporary mathematics.
Sets are of great importance in mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
; in fact, in modern formal treatments, most mathematical objects (number
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s, relations
Relation (mathematics)
In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...
, functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, etc.) are defined in terms of sets. Naive set theory can be seen as a stepping-stone to more formal treatments, and suffices for many purposes.
Requirements
In the sense of this article, a naive theory is a non-formalized theory, that is, a theory that uses a natural languageNatural language
In the philosophy of language, a natural language is any language which arises in an unpremeditated fashion as the result of the innate facility for language possessed by the human intellect. A natural language is typically used for communication, and may be spoken, signed, or written...
to describe sets. The words and, or, if ... then, not, for some, for every are not subject to rigorous definition. It is useful to study sets naively at an early stage of mathematics in order to develop facility for working with them. Furthermore, a firm grasp of set theoretical concepts from a naive standpoint is important as a first stage in understanding the motivation for the formal axioms of set theory.
This article develops a naive theory. Sets are defined informally and a few of their properties are investigated. Links in this article to specific axioms of set theory describe some of the relationships between the informal discussion here and the formal axiomatization of set theory, but no attempt is made to justify every statement on such a basis. The first development of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
was a naive set theory. It was created at the end of the 19th century by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
as part of his study of infinite sets.
As it turned out, assuming that one can perform any operation on sets without restriction leads to paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es such as Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
and Berry's paradox. Some believe that Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
's set theory was not actually implicated by these paradox
Paradox
Similar to Circular reasoning, A paradox is a seemingly true statement or group of statements that lead to a contradiction or a situation which seems to defy logic or intuition...
es (see Frápolli 1991); one difficulty in determining this with certainty is that Cantor did not provide an axiomatization of his system. It is undisputed that, by 1900, Cantor was aware of some of the paradoxes and did not believe that they discredited his theory. Gottlob Frege
Gottlob Frege
Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...
did explicitly axiomatize a theory in which the formalized version of naive set theory can be interpreted, and it is this formal theory which Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
actually addressed when he presented his paradox.
Axiomatic set theory was developed in response to these early attempts to study set theory, with the goal of determining precisely what operations were allowed and when. Today, when mathematicians talk about "set theory" as a field, they usually mean axiomatic set theory. Informal applications of set theory in other fields are sometimes referred to as applications of "naive set theory", but usually are understood to be justifiable in terms of an axiomatic system
Axiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
(normally the Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
).
A naive set theory is not necessarily inconsistent, if it correctly specifies the sets allowed to be considered. This can be done by the means of definitions, which are implicit axioms. It can be done by systematically making explicit all the axioms, as in the case of the well-known book Naive Set Theory by Paul Halmos
Paul Halmos
Paul Richard Halmos was a Hungarian-born American mathematician who made fundamental advances in the areas of probability theory, statistics, operator theory, ergodic theory, and functional analysis . He was also recognized as a great mathematical expositor.-Career:Halmos obtained his B.A...
, which is actually a somewhat (not all that) informal presentation of the usual axiomatic Zermelo–Fraenkel set theory
Zermelo–Fraenkel set theory
In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...
. It is 'naive' in that the language and notations are those of ordinary informal mathematics, and in that it doesn't deal with consistency or completeness of the axiom system. However, the term naive set theory is also used in some literature to refer to the set theories studied by Frege and Cantor, rather than to the informal counterparts of modern axiomatic set theory; care is required to tell which sense is intended.
Sets, membership and equality
In naive set theory, a set is described as a well-defined collection of objects. These objects are called the elements or members of the set. Objects can be anything: numbers, people, other sets, etc. For instance, 4 is a member of the set of all even integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. Clearly, the set of even numbers is infinitely large; there is no requirement that a set be finite.
If x is a member of A, then it is also said that x belongs to A, or that x is in A. In this case, we write x ∈ A.
(The symbol ∈ is a derivation from the Greek letter
Greek alphabet
The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...
epsilon
Epsilon
Epsilon is the fifth letter of the Greek alphabet, corresponding phonetically to a close-mid front unrounded vowel . In the system of Greek numerals it has a value of 5. It was derived from the Phoenician letter He...
, "ε", introduced by Peano in 1888.)
The symbol ∉ is sometimes used to write x ∉ A, meaning "x is not in A".
Two sets A and B are defined to be equal when they have precisely the same elements, that is, if every element of A is an element of B and every element of B is an element of A. (See axiom of extensionality
Axiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
.) Thus a set is completely determined by its elements; the description is immaterial. For example, the set with elements 2, 3, and 5 is equal to the set of all prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s less than 6.
If the sets A and B are equal, this is denoted symbolically as A = B (as usual).
We also allow for an empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, often denoted Ø and sometimes : a set without any members at all.
Since a set is determined completely by its elements, there can only be one empty set. (See axiom of empty set
Axiom of empty set
In axiomatic set theory, the axiom of empty set is an axiom of Zermelo–Fraenkel set theory, the fragment thereof Burgess calls ST, and Kripke–Platek set theory.- Formal statement :...
.) Note that Ø ≠ {Ø}.
Specifying sets
The simplest way to describe a set is to list its elements between curly braces (known as defining a set extensionally). Thus {1,2} denotes the set whose only elements are 1 and 2.(See axiom of pairing
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
.)
Note the following points:
- Order of elements is immaterial; for example, {1,2} = {2,1}.
- Repetition (multiplicityMultiplicity (mathematics)In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
) of elements is irrelevant; for example, {1,2,2} = {1,1,1,2} = {1,2}.
(These are consequences of the definition of equality in the previous section.)
This notation can be informally abused by saying something like {dogs} to indicate the set of all dogs, but this example would usually be read by mathematicians as "the set containing the single element dogs".
An extreme (but correct) example of this notation is {}, which denotes the empty set.
We can also use the notation {x : P(x)}, or sometimes {x | P(x)}, to denote the set containing all objects for which the condition P holds (known as defining a set intensionally).
For example, {x : x is a real number} denotes the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, {x : x has blonde hair} denotes the set of everything with blonde hair, and {x : x is a dog} denotes the set of all dogs.
This notation is called set-builder notation
Set-builder notation
In set theory and its applications to logic, mathematics, and computer science, set-builder notation is a mathematical notation for describing a set by stating the properties that its members must satisfy...
(or "set comprehension", particularly in the context of Functional programming
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
).
Some variants of set builder notation are:
- {x ∈ A : P(x)} denotes the set of all x that are already members of A such that the condition P holds for x. For example, if Z is the set of integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s, then {x ∈ Z : x is even} is the set of all evenEven and odd numbersIn mathematics, the parity of an object states whether it is even or odd.This concept begins with integers. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2...
integers. (See axiom of specification.) - {F(x) : x ∈ A} denotes the set of all objects obtained by putting members of the set A into the formula F. For example, {2x : x ∈ Z} is again the set of all even integers. (See axiom of replacement.)
- {F(x) : P(x)} is the most general form of set builder notation. For example, {xs owner : x is a dog} is the set of all dog owners.
Subsets
Given two sets A and B we say that A is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of B if every element of A is also an element of B.
Notice that in particular, B is a subset of itself; a subset of B that isn't equal to B is called a proper subset.
If A is a subset of B, then one can also say that B is a superset of A, that A is contained in B, or that B contains A.
In symbols, A ⊆ B means that A is a subset of B, and B ⊇ A means that B is a superset of A.
Some authors use the symbols "⊂" and "⊃" for subsets, and others use these symbols only for proper subsets. For clarity, one can explicitly use the symbols "
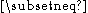 " and "
" and "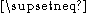 " to indicate non-equality.
" to indicate non-equality.As an illustration, let R be the set of real numbers, let Z be the set of integers, let O be the set of odd integers, and let P be the set of current or former U.S. Presidents
President of the United States
The President of the United States of America is the head of state and head of government of the United States. The president leads the executive branch of the federal government and is the commander-in-chief of the United States Armed Forces....
.
Then O is a subset of Z, Z is a subset of R, and (hence) O is a subset of R, where in all cases subset may even be read as proper subset.
Note that not all sets are comparable in this way.
For example, it is not the case either that R is a subset of P nor that P is a subset of R.
It follows immediately from the definition of equality of sets above that, given two sets A and B, A = B if and only if A ⊆ B and B ⊆ A. In fact this is often given as the definition of equality. Usually when trying to prove
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
that two sets are equal, one aims to show these two inclusions. Note that the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
is a subset of every set (the statement that all elements of the empty set are also members of any set A is vacuously true).
The set of all subsets of a given set A is called the power set of A and is denoted by
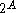 or
or 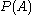 ; the "P" is sometimes in a fancy font. If the set A has n elements, then
; the "P" is sometimes in a fancy font. If the set A has n elements, then 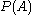 will have
will have  elements.
elements.Universal sets and absolute complements
In certain contexts we may consider all sets under consideration as being subsets of some given universal setUniverse (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
.
For instance, if we are investigating properties of the real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s R (and subsets of R), then we may take R as our universal set. A universal set is only temporarily defined by the context; there is no such thing as a "universal" universal set, "the set of everything" (see Paradoxes below).
Given a universal set U and a subset A of U, we may define the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of A (in U) as
- AC := {x
In other words, AC ("A-complement"; sometimes simply A, "A-prime" ) is the set of all members of U which are not members of A.
Thus with R, Z and O defined as in the section on subsets, if Z is the universal set, then OC is the set of even integers, while if R is the universal set, then OC is the set of all real numbers that are either even integers or not integers at all.
Unions, intersections, and relative complements
Given two sets A and B, we may construct their unionUnion (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
.
This is the set consisting of all objects which are elements of A or of B or of both (see axiom of union
Axiom of union
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of union is one of the axioms of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x...
). It is denoted by A ∪ B.
The intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
of A and B is the set of all objects which are both in A and in B. It is denoted by A ∩ B.
Finally, the relative complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of B relative to A, also known as the set theoretic difference of A and B, is the set of all objects that belong to A but not to B. It is written as A \ B or A − B.
Symbolically, these are respectively
- A ∪ B := {x : (x ∈ A) orLogical disjunctionIn logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
(x ∈ B)}; - A ∩ B := {x : (x ∈ A) andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
(x ∈ B)} = {x ∈ A : x ∈ B} = {x ∈ B : x ∈ A}; - A \ B := {x : (x ∈ A) and notNegationIn logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
(x ∈ B) } = {x ∈ A : not (x ∈ B)}.
Notice that A doesn't have to be a subset of B for B \ A to make sense; this is the difference between the relative complement and the absolute complement from the previous section.
To illustrate these ideas, let A be the set of left-handed people, and let B be the set of people with blond hair.
Then A ∩ B is the set of all left-handed blond-haired people, while A ∪ B is the set of all people who are left-handed or blond-haired or both.
A \ B, on the other hand, is the set of all people that are left-handed but not blond-haired, while B \ A is the set of all people who have blond hair but aren't left-handed.
Now let E be the set of all human beings, and let F be the set of all living things over 1000 years old.
What is E ∩ F in this case?
No living human being is over 1000 years old
Oldest people
This is a list of tables of the verified oldest people in the world in ordinal rank, such as oldest person or oldest man. In these tables, a supercentenarian is considered 'verified' if his or her claim has been validated by an international body that specifically deals in longevity research, such...
, so E ∩ F must be the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
{}.
For any set A, the power set
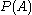 is a Boolean algebra under the operations of union and intersection.
is a Boolean algebra under the operations of union and intersection.Ordered pairs and Cartesian products
Intuitively, an ordered pairOrdered pair
In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...
is simply a collection of two objects such that one can be distinguished as the first element and the other as the second element, and having the fundamental property that, two ordered pairs are equal if and only if their first elements are equal and their second elements are equal.
Formally, an ordered pair with first coordinate a, and second coordinate b, usually denoted by (a, b), can be defined as the set .
It follows that, two ordered pairs (a,b) and (c,d) are equal if and only if a = c and b = d.
Alternatively, an ordered pair can be formally thought of as a set {a,b} with a total order
Total order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
.
(The notation (a, b) is also used to denote an open interval on the real number line, but the context should make it clear which meaning is intended. Otherwise, the notation ]a, b[ may be used to denote the open interval whereas (a, b) is used for the ordered pair).
If A and B are sets, then the Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
(or simply product) is defined to be:
- A × B = {(a,b) : a is in A and b is in B}.
That is, A × B is the set of all ordered pairs whose first coordinate is an element of A and whose second coordinate is an element of B.
We can extend this definition to a set A × B × C of ordered triples, and more generally to sets of ordered n-tuples for any positive integer n.
It is even possible to define infinite Cartesian product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
s, but to do this we need a more recondite definition of the product.
Cartesian products were first developed by René Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
in the context of analytic geometry
Analytic geometry
Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...
.
If R denotes the set of all real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, then R2 := R × R represents the Euclidean plane and R3 := R × R × R represents three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
.
Some important sets
Note: In this section, a, b, and c are natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, and r and s are real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
- Natural numberNatural numberIn mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s are used for counting. A blackboard boldBlackboard boldBlackboard bold is a typeface style that is often used for certain symbols in mathematical texts, in which certain lines of the symbol are doubled. The symbols usually denote number sets...
capital N (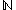 ) often represents this set.
) often represents this set. - IntegerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s appear as solutions for x in equations like x + a = b. A blackboard bold capital Z ( ) often represents this set (from the German Zahlen, meaning numbers).
) often represents this set (from the German Zahlen, meaning numbers). - Rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s appear as solutions to equations like a + bx = c. A blackboard bold capital Q ( ) often represents this set (for quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
) often represents this set (for quotientQuotientIn mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
, because R is used for the set of real numbers). - Algebraic numberAlgebraic numberIn mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
s appear as solutions to polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
equations (with integer coefficients) and may involve radicalsNth rootIn mathematics, the nth root of a number x is a number r which, when raised to the power of n, equals xr^n = x,where n is the degree of the root...
and certain other irrational numberIrrational numberIn mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s. A blackboard bold capital A ( ) or a Q with an overline (
) or a Q with an overline ( ) often represents this set. The overline denotes the operation of algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
) often represents this set. The overline denotes the operation of algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
. - Real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s represent the "real line" and include all numbers that can be approximated by rationals. These numbers may be rational or algebraic but may also be transcendental numberTranscendental numberIn mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
s, which cannot appear as solutions to polynomial equations with rational coefficients. A blackboard bold capital R ( ) often represents this set.
) often represents this set. - Complex numberComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s are sums of a real and an imaginary number: r + si. Here both r and s can equal zero; thus, the set of real numbers and the set of imaginary numbers are subsets of the set of complex numbers, which form an algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
for the set of real numbers, meaning that every polynomial with coefficients in has at least one root in this set. A blackboard bold capital C (
has at least one root in this set. A blackboard bold capital C (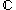 ) often represents this set. Note that since a number r + si can be identified with a point (r, s) in the plane, C is basically "the same" as the Cartesian product R×R ("the same" meaning that any point in one determines a unique point in the other and for the result of calculations it doesn't matter which one is used for the calculation).
) often represents this set. Note that since a number r + si can be identified with a point (r, s) in the plane, C is basically "the same" as the Cartesian product R×R ("the same" meaning that any point in one determines a unique point in the other and for the result of calculations it doesn't matter which one is used for the calculation).
Paradoxes
We referred earlier to the need for a formal, axiomatic approach. What problems arise in the treatment we have given? The problems relate to the formation of sets. One's first intuition might be that we can form any set we want, but this view leads to inconsistencies. For any set x we can ask whether x is a member of itself. Define- Z = {x : x is not a member of x}.
Now for the problem: is Z a member of Z? If yes, then by the defining quality of Z, Z is not a member of itself, i.e., Z is not a member of Z. This forces us to declare that Z is not a member of Z. Then Z is not a member of itself and so, again by definition of Z, Z is a member of Z.
Thus both options lead us to a contradiction and we have an inconsistent theory. More succinctly, one says that Z is a member of Z if and only if Z is not a member of Z. Axiomatic developments place restrictions on the sort of sets we are allowed to form and thus prevent problems like our set Z from arising. This particular paradox is Russell's paradox
Russell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
.
The penalty is that one must take more care with one's development, as one must in any rigorous mathematical argument.
In particular, it is problematic to speak of a set of everything, or to be (possibly) a bit less ambitious, even a set of all sets.
In fact, in the standard axiomatisation of set theory, there is no set of all sets.
In areas of mathematics that seem to require a set of all sets (such as category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
), one can sometimes make do with a universal set so large that all of ordinary mathematics can be done within it (see universe
Universe (mathematics)
In mathematics, and particularly in set theory and the foundations of mathematics, a universe is a class that contains all the entities one wishes to consider in a given situation...
).
Alternatively, one can make use of proper classes
Class (set theory)
In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
.
Or, one can use a different axiomatisation of set theory, such as W. V. Quine's New Foundations
New Foundations
In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...
, which allows for a set of all sets and avoids Russell's paradox in another way.
See also
- Algebra of setsAlgebra of setsThe algebra of sets develops and describes the basic properties and laws of sets, the set-theoretic operations of union, intersection, and complementation and the relations of set equality and set inclusion...
- Axiomatic set theory
- Internal set theoryInternal set theoryInternal set theory is a mathematical theory of sets developed by Edward Nelson that provides an axiomatic basis for a portion of the non-standard analysis introduced by Abraham Robinson. Instead of adding new elements to the real numbers, the axioms introduce a new term, "standard", which can be...
- Set theorySet theorySet theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
- Set (mathematics)
- Partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
External links
- Beginnings of set theory page at St. Andrews
- Earliest Known Uses of Some of the Words of Mathematics (S)
- Uniqueness of the empty set Is there only one empty set rather than an infinity of empty subsets?

