
Axiom of extensionality
Encyclopedia
In axiomatic set theory and the branches of logic
, mathematics
, and computer science
that use it, the axiom of extensionality, or axiom of extension, is one of the axiom
s of Zermelo-Fraenkel set theory.
of the Zermelo-Fraenkel axioms, the axiom reads:
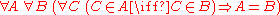
or in words:
(It is not really essential that C here be a set — but in ZF, everything is. See Ur-elements below for when this is violated.)
The converse,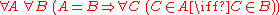 , of this axiom follows from the substitution property of equality.
, of this axiom follows from the substitution property of equality.
Thus, what the axiom is really saying is that two sets are equal if and only if
they have precisely the same members.
The essence of this is:
The axiom of extensionality can be used with any statement of the form
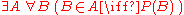 ,
,
where P is any unary predicate that does not mention A, to define a unique set whose members are precisely the sets satisfying the predicate
whose members are precisely the sets satisfying the predicate 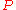 .
.
We can then introduce a new symbol for ; it's in this way that definition
; it's in this way that definition
s in ordinary mathematics ultimately work when their statements are reduced to purely set-theoretic terms.
The axiom of extensionality is generally uncontroversial in set-theoretical foundations of mathematics, and it or an equivalent appears in just about any alternative axiomatisation of set theory.
However, it may require modifications for some purposes, as below.
.
Some treatments of axiomatic set theory prefer to do without this, and instead treat the above statement not as an axiom but as a definition of equality.
Then it is necessary to include the usual axioms of equality from predicate logic as axioms about this defined symbol. Most of the axioms of equality still follow from the definition; the remaining one is
and it becomes this axiom that is referred to as the axiom of extensionality in this context.
is a member of a set that is not itself a set.
In the Zermelo-Fraenkel axioms, there are no ur-elements, but they are included in some alternative axiomatisations of set theory.
Ur-elements can be treated as a different logical type from sets; in this case,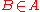 makes no sense if
makes no sense if  is an ur-element, so the axiom of extensionality simply applies only to sets.
is an ur-element, so the axiom of extensionality simply applies only to sets.
Alternatively, in untyped logic, we can require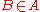 to be false whenever
to be false whenever  is an ur-element.
is an ur-element.
In this case, the usual axiom of extensionality would then imply that every ur-element is equal to the empty set
.
To avoid this consequence, we can modify the axiom of extensionality to apply only to nonempty sets, so that it reads:
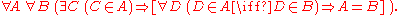
That is:
Yet another alternative in untyped logic is to define itself to be the only element of
itself to be the only element of 
whenever is an ur-element. While this approach can serve to preserve the axiom of extensionality, the axiom of regularity
is an ur-element. While this approach can serve to preserve the axiom of extensionality, the axiom of regularity
will need an adjustment instead.
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that use it, the axiom of extensionality, or axiom of extension, is one of the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of Zermelo-Fraenkel set theory.
Formal statement
In the formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the Zermelo-Fraenkel axioms, the axiom reads:
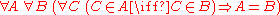
or in words:
- Given any set A and any set B, if for every set C, C is a member of A if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
C is a member of B, then A is equal to B.
(It is not really essential that C here be a set — but in ZF, everything is. See Ur-elements below for when this is violated.)
The converse,
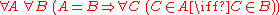 , of this axiom follows from the substitution property of equality.
, of this axiom follows from the substitution property of equality.Interpretation
To understand this axiom, note that the clause in parentheses in the symbolic statement above simply states that A and B have precisely the same members.Thus, what the axiom is really saying is that two sets are equal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
they have precisely the same members.
The essence of this is:
- A set is determined uniquely by its members.
The axiom of extensionality can be used with any statement of the form
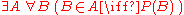 ,
,where P is any unary predicate that does not mention A, to define a unique set
 whose members are precisely the sets satisfying the predicate
whose members are precisely the sets satisfying the predicate 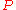 .
.We can then introduce a new symbol for
 ; it's in this way that definition
; it's in this way that definitionDefinition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
s in ordinary mathematics ultimately work when their statements are reduced to purely set-theoretic terms.
The axiom of extensionality is generally uncontroversial in set-theoretical foundations of mathematics, and it or an equivalent appears in just about any alternative axiomatisation of set theory.
However, it may require modifications for some purposes, as below.
In predicate logic without equality
The axiom given above assumes that equality is a primitive symbol in predicate logicPredicate logic
In mathematical logic, predicate logic is the generic term for symbolic formal systems like first-order logic, second-order logic, many-sorted logic or infinitary logic. This formal system is distinguished from other systems in that its formulae contain variables which can be quantified...
.
Some treatments of axiomatic set theory prefer to do without this, and instead treat the above statement not as an axiom but as a definition of equality.
Then it is necessary to include the usual axioms of equality from predicate logic as axioms about this defined symbol. Most of the axioms of equality still follow from the definition; the remaining one is

and it becomes this axiom that is referred to as the axiom of extensionality in this context.
In set theory with ur-elements
An ur-elementUr-element
In set theory, a branch of mathematics, an urelement or ur-element is an object which is not a set, but that may be an element of a set...
is a member of a set that is not itself a set.
In the Zermelo-Fraenkel axioms, there are no ur-elements, but they are included in some alternative axiomatisations of set theory.
Ur-elements can be treated as a different logical type from sets; in this case,
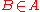 makes no sense if
makes no sense if  is an ur-element, so the axiom of extensionality simply applies only to sets.
is an ur-element, so the axiom of extensionality simply applies only to sets.Alternatively, in untyped logic, we can require
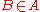 to be false whenever
to be false whenever  is an ur-element.
is an ur-element.In this case, the usual axiom of extensionality would then imply that every ur-element is equal to the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
.
To avoid this consequence, we can modify the axiom of extensionality to apply only to nonempty sets, so that it reads:
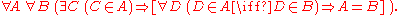
That is:
- Given any set A and any set B, if A is a nonempty set (that is, if there exists a member C of A), then if A and B have precisely the same members, then they are equal.
Yet another alternative in untyped logic is to define
 itself to be the only element of
itself to be the only element of 
whenever
 is an ur-element. While this approach can serve to preserve the axiom of extensionality, the axiom of regularity
is an ur-element. While this approach can serve to preserve the axiom of extensionality, the axiom of regularityAxiom of regularity
In mathematics, the axiom of regularity is one of the axioms of Zermelo-Fraenkel set theory and was introduced by...
will need an adjustment instead.

