Set-builder notation
Encyclopedia
In set theory
and its applications to logic
, mathematics
, and computer science
, set-builder notation (sometimes simply set notation
) is a mathematical notation
for describing a set by stating the properties that its members must satisfy. Forming sets in this manner is also known as set comprehension, set abstraction or as defining a set's intension
.
in which x appears free. Set builder notation has the form {x : Φ(x)} (or {x | Φ(x}) according to the international standard ISO 31-11
using the vertical bar
instead of the colon), denoting the set of all individuals in the universe of discourse satisfying the formula Φ(x), that is, the set whose members are every individual x such that Φ(x) is true: formally, the extension
of the predicate. Sometimes the universe of discourse is established within the notation; writing {x ∈ U : Φ(x)} establishes that the universe of discourse is U, for purposes of the set being built. Set builder notation binds the variable x and must be used with the same care applied to variables bound by quantifiers.
Examples (the universe of discourse can be taken to be the set of real number
s, where not specified inside the notation):
The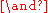
sign stands for and, requiring both conditions be fulfilled simultaneously. It is often replaced by a comma semicolon or written out as and.
The
sign denotes set membership, and can be read as "in".
.
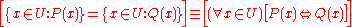This means that two sets are equal if and only if
their "membership requirements" are logically equivalent.
For example,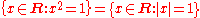
because, for any real number x, x2 = 1 if and only if |x| = 1; and, therefore, both constructions produce the same set {-1,1}.
denote the set R of all sets S that do not belong to themselves. The inconsistency of the existence of this set is known as Russell's paradox
.
Solutions to the paradox restrict the notion of set construction in some way. To illustrate this in terms of our notation, let X = {x ∈ A : P(x)} denote the set of every element of A satisfying the predicate P(x). The canonical restriction on set builder notation asserts that X is a set only if A is already known to be a set. This restriction is codified in the axiom schema of separation present in standard axiomatic set theory. Note that this axiom schema
excludes R from sethood.
As the last example shows, such an abbreviated notation again might not denote an actual nonparadoxical set, unless there is in fact a set of all objects that might be described by the variable in question.
For example:
, the set of all x (in a universe of discourse A) satisfying the condition P(x) would be written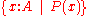
. In Z, an element x's set membership is written as 
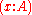instead of 
, the vertical bar is used to indicate a predicate. Versions of set builder notation are also available in Z which allow for terms more complicated than a single variable, using a bullet to indicate the form of members of the set. So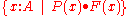 
denotes the set of all values F(x), where x is in A and P(x) holds.
and Haskell
) is the list comprehension, which combines map
and filter
operations over one or more lists.
Python replaces set-builder's braces with square brackets and uses a language-based syntax. Haskell replaces set-builder's braces with square brackets and uses symbolic constructs, including the standard set-builder vertical bar. Consider these examples given in set-builder notation, Python, and Haskell:
The set builder notation and list comprehension notation are both instances of a more general notation known as monad comprehensions, which permits map/filter-like operations over any monad with a zero element
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
and its applications to logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, set-builder notation (sometimes simply set notation
Set notation
Sets are fundamental objects in mathematics. Intuitively, a set is merely a collection of elements or members. There are various conventions for textually denoting sets...
) is a mathematical notation
Mathematical notation
Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...
for describing a set by stating the properties that its members must satisfy. Forming sets in this manner is also known as set comprehension, set abstraction or as defining a set's intension
Intension
In linguistics, logic, philosophy, and other fields, an intension is any property or quality connoted by a word, phrase or other symbol. In the case of a word, it is often implied by the word's definition...
.
Building sets
Let Φ(x) be a formulaWell-formed formula
In mathematical logic, a well-formed formula, shortly wff, often simply formula, is a word which is part of a formal language...
in which x appears free. Set builder notation has the form {x : Φ(x)} (or {x | Φ(x}) according to the international standard ISO 31-11
ISO 31-11
ISO 31-11 was the part of international standard ISO 31 that defines mathematical signs and symbols for use in physical sciences and technology...
using the vertical bar
Vertical bar
The vertical bar is a character with various uses in mathematics, where it can be used to represent absolute value, among others; in computing and programming and in general typography, as a divider not unlike the interpunct...
instead of the colon), denoting the set of all individuals in the universe of discourse satisfying the formula Φ(x), that is, the set whose members are every individual x such that Φ(x) is true: formally, the extension
Extension (predicate logic)
The extension of a predicatea truth-valued functionis the set of tuples of values that, used as arguments, satisfy the predicate. Such a set of tuples is a relation.For example the statement "d2 is the weekday following d1"...
of the predicate. Sometimes the universe of discourse is established within the notation; writing {x ∈ U : Φ(x)} establishes that the universe of discourse is U, for purposes of the set being built. Set builder notation binds the variable x and must be used with the same care applied to variables bound by quantifiers.
Examples (the universe of discourse can be taken to be the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, where not specified inside the notation):
-
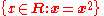is the set 
, -
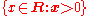is the set of all positive real numbers. -
is the set of all even natural numbers, -
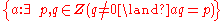is the set of rational numberRational numberIn mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s; that is, numbers that can be written as the ratio of two integers. -
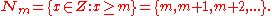Thus, e.g., 
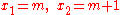, etc. (n.b.Nota BeneNota bene is an Italian and Latin phrase meaning "note well". The phrase first appeared in writing circa 1721.Often abbreviated as "N. B.", nota bene comes from the Latin roots notāre and bene . It is in the singular imperative mood, instructing one individual to note well the matter at hand...
: in the case of sets, the order is not important;
could be used). As an example,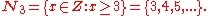 
The
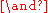sign stands for and, requiring both conditions be fulfilled simultaneously. It is often replaced by a comma semicolon or written out as and.The
sign denotes set membership, and can be read as "in".Logical equivalence
Logical equivalence is an important concept in set-builder notation: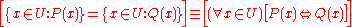.This means that two sets are equal if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
their "membership requirements" are logically equivalent.
For example,
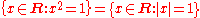because, for any real number x, x2 = 1 if and only if |x| = 1; and, therefore, both constructions produce the same set {-1,1}.Russell's paradox
Let denote the set R of all sets S that do not belong to themselves. The inconsistency of the existence of this set is known as Russell's paradoxRussell's paradox
In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...
.
Solutions to the paradox restrict the notion of set construction in some way. To illustrate this in terms of our notation, let X = {x ∈ A : P(x)} denote the set of every element of A satisfying the predicate P(x). The canonical restriction on set builder notation asserts that X is a set only if A is already known to be a set. This restriction is codified in the axiom schema of separation present in standard axiomatic set theory. Note that this axiom schema
Axiom schema
In mathematical logic, an axiom schema generalizes the notion of axiom.An axiom schema is a formula in the language of an axiomatic system, in which one or more schematic variables appear. These variables, which are metalinguistic constructs, stand for any term or subformula of the system, which...
excludes R from sethood.
Other problems
The notation can be complicated, especially as in the previous example, and abbreviations are often employed when context indicates the nature of a variable. For example:- {x : x > 0}, in a context where the variable x is used only for real numbers, indicates the set of all positive real numbers;
- {p/q : q ≠ 0}, in a context where the variables p and q are used only for integers, indicates the set of all rational numbers; and
- {S : S does not belong to S}, in a context where the variable S is used only for sets, indicates the set of all sets that don't belong to themselves.
As the last example shows, such an abbreviated notation again might not denote an actual nonparadoxical set, unless there is in fact a set of all objects that might be described by the variable in question.
Terms more complicated than a single variable
Another variation on set-builder notation replaces the single variable x with a term T which may include one or more variables, combined with functions acting on them. So instead of {x : Φ(x)}, we would have {T : Φ(x1 ... xn)}, where T is a term involving variables x1 through xn.For example:
- {2n : n ∈ N}, where N is the set of all natural numbers, is the set of all even natural numbers.
- {p/q : p,q ∈ Z, q≠0}, where Z is the set of all integers, is the set of all rational numbers (Q).
Z notation
In Z notationZ notation
The Z notation , named after Zermelo–Fraenkel set theory, is a formal specification language used for describing and modelling computing systems. It is targeted at the clear specification of computer programs and computer-based systems in general.-History:...
, the set of all x (in a universe of discourse A) satisfying the condition P(x) would be written
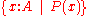. In Z, an element x's set membership is written as 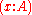instead of , the vertical bar is used to indicate a predicate. Versions of set builder notation are also available in Z which allow for terms more complicated than a single variable, using a bullet to indicate the form of members of the set. So 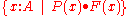denotes the set of all values F(x), where x is in A and P(x) holds.Parallels in programming languages
A similar notation available in a number of programming languages (notably PythonPython (programming language)
Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
and Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
) is the list comprehension, which combines map
Map (higher-order function)
In many programming languages, map is the name of a higher-order function that applies a given function to each element of a list, returning a list of results. They are examples of both catamorphisms and anamorphisms...
and filter
Filter (higher-order function)
In functional programming, filter is a higher-order function that processes a data structure in some order to produce a new data structure containing exactly those elements of the original data structure for which a given predicate returns the boolean value true.-Example:In Haskell, the code...
operations over one or more lists.
Python replaces set-builder's braces with square brackets and uses a language-based syntax. Haskell replaces set-builder's braces with square brackets and uses symbolic constructs, including the standard set-builder vertical bar. Consider these examples given in set-builder notation, Python, and Haskell:
| Example 1 | Example 2 | |
|---|---|---|
| Set-builder | ||
| Python Python (programming language) Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive... |
|
|
| Haskell Haskell (programming language) Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the... |
[l > l <- ls] | [(k, x) > k <- ks, x <- xs, p x] |
The set builder notation and list comprehension notation are both instances of a more general notation known as monad comprehensions, which permits map/filter-like operations over any monad with a zero element
Zero element
In mathematics, a zero element is one of several generalizations of the number zero to other algebraic structures. These alternate meanings may or may not reduce to the same thing, depending on the context.-Additive identities:...
.