
Axiom of union
Encyclopedia
In axiomatic set theory and the branches of logic
, mathematics
, and computer science
that use it, the axiom of union is one of the axiom
s of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x. Together with the axiom of pairing
this implies that for any two sets, there is a set that contains exactly the elements of both.
of the Zermelo-Fraenkel axioms, the axiom reads: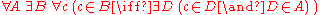
or in words:
this set B is unique and it is called the union
of A, and denoted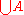 . Thus the essence of the axiom is:
. Thus the essence of the axiom is:
The axiom of union is generally considered uncontroversial, and it or an equivalent appears in just about any alternative axiomatization of set theory.
Note that there is no corresponding axiom of intersection
. If A is a nonempty set containing E, then we can form the intersection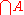 using the axiom schema of specification
using the axiom schema of specification
as
so no separate axiom of intersection is necessary. (If A is the empty set
, then trying to form the intersection of A as
is not permitted by the axioms. Moreover, if such a set existed, then it would contain every set in the "universe", but the notion of a universal set
is antithetical to Zermelo–Fraenkel set theory.)
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
, mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that use it, the axiom of union is one of the axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s of Zermelo-Fraenkel set theory, stating that, for any set x there is a set y whose elements are precisely the elements of the elements of x. Together with the axiom of pairing
Axiom of pairing
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of pairing is one of the axioms of Zermelo–Fraenkel set theory.- Formal statement :...
this implies that for any two sets, there is a set that contains exactly the elements of both.
Formal statement
In the formal languageFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
of the Zermelo-Fraenkel axioms, the axiom reads:
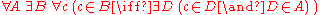
or in words:
- Given any set A, there isExistential quantificationIn predicate logic, an existential quantification is the predication of a property or relation to at least one member of the domain. It is denoted by the logical operator symbol ∃ , which is called the existential quantifier...
a set B such that, for any element c, c is a member of B if and only ifIf and only ifIn logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is a set D such that c is a member of D andLogical conjunctionIn logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
D is a member of A.
Interpretation
What the axiom is really saying is that, given a set A, we can find a set B whose members are precisely the members of the members of A. By the axiom of extensionalityAxiom of extensionality
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom of extensionality, or axiom of extension, is one of the axioms of Zermelo-Fraenkel set theory.- Formal statement :...
this set B is unique and it is called the union
Union (set theory)
In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
of A, and denoted
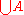 . Thus the essence of the axiom is:
. Thus the essence of the axiom is:
- The union of a set is a set.
The axiom of union is generally considered uncontroversial, and it or an equivalent appears in just about any alternative axiomatization of set theory.
Note that there is no corresponding axiom of intersection
Intersection (set theory)
In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....
. If A is a nonempty set containing E, then we can form the intersection
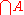 using the axiom schema of specification
using the axiom schema of specificationAxiom schema of specification
In axiomatic set theory and the branches of logic, mathematics, and computer science that use it, the axiom schema of specification, axiom schema of separation, subset axiom scheme or axiom schema of restricted comprehension, is a schema of axioms in Zermelo-Fraenkel set theory...
as
- {c in E: for all D in A, c is in D},
so no separate axiom of intersection is necessary. (If A is the empty set
Empty set
In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
, then trying to form the intersection of A as
- {c: for all D in A, c is in D}
is not permitted by the axioms. Moreover, if such a set existed, then it would contain every set in the "universe", but the notion of a universal set
Universal set
In set theory, a universal set is a set which contains all objects, including itself. In set theory as usually formulated, the conception of a set of all sets leads to a paradox...
is antithetical to Zermelo–Fraenkel set theory.)

