
Even and odd numbers
Encyclopedia
In mathematics
, the parity of an object states whether it is even or odd.
This concept begins with integer
s. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2. (The old-fashioned term "evenly divisible" is now almost always shortened to "divisible".) A formal definition of an even number is that it is an integer of the form n = 2k, where k is an integer; it can then be shown that an odd number is an integer of the form n = 2k + 1.
Examples of even numbers are −4, 8, and 1728. Examples of odd numbers are −5, 9, 3, and 71. This classification only applies to integers, i.e., a fractional number like 1/2 or 4.201 is neither even nor odd.
The sets of even and odd numbers can be defined as following:
A number (i.e., integer) expressed in the decimal
numeral system
is even or odd according to whether its last digit is even or odd.
That is, if the last digit is 1, 3, 5, 7, or 9, then it's odd; otherwise it's even. The same idea will work using any even base.
In particular, a number expressed in the binary numeral system
is odd if its last digit is 1 and even if its last digit is 0.
In an odd base, the number is even according to the sum of its digits – it is even if and only if the sum of its digits is even.
, and are commonly used to check if an equality is likely to be correct by testing the parity of each side. As with ordinary arithmetic, multiplication and addition are commutative and associative, and multiplication is distributive over addition. However, subtraction in parity is identical to addition, so subtraction also possesses these properties (which are absent from ordinary arithmetic).
Addition
Rules analogous to these for divisibility by 9 are used in the method of casting out nines
.
Division
The division of two whole numbers does not necessarily result in a whole number.
For example, 1 divided by 4 equals 1/4, which is neither even nor odd, since the concepts even and odd apply only to integers.
But when the quotient
is an integer, it will be even if and only if
the dividend
has more factors of two
than the divisor.
s with a cylindrical bore and in effect closed at one end, such as the clarinet
at the mouthpiece, the harmonic
s produced are odd multiples of the fundamental frequency
. (With cylindrical pipes open at both ends, used for example in some organ stop
s such as the open diapason, the harmonics are even multiples of the same frequency for the given bore length, but this has the effect of the fundamental frequency being doubled and all multiples of this fundamental frequency being produced.) See harmonic series (music)
.
element for addition, zero, is an element of the even numbers only. An integer is even if it is congruent to 0 modulo
this ideal, in other words if it is congruent to 0 modulo 2, and odd if it is congruent to 1 modulo 2.
All prime number
s are odd, with one exception: the prime number 2. All known perfect number
s are even; it is unknown whether any odd perfect numbers exist.
The squares of all even numbers are even, and the squares of all odd numbers are odd. Since an even number can be expressed as 2x, (2x)2 = 4x2 which is even. Since an odd number can be expressed as 2x + 1, (2x + 1)2 = 4x2 + 4x + 1. 4x2 and 4x are even, which means that 4x2 + 4x + 1 is odd (since even + odd = odd).
Goldbach's conjecture
states that every even integer greater than 2 can be represented as a sum of two prime numbers.
Modern computer
calculations have shown this conjecture to be true for integers up to at least 4 × 1014, but still no general proof
has been found.
The Feit–Thompson theorem states that a finite group
is always solvable if its order is an odd number. This is an example of odd numbers playing a role in an advanced mathematical theorem where the method of application of the simple hypothesis of "odd order" is far from obvious.

Parity is also used to refer to a number of other properties.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the parity of an object states whether it is even or odd.
This concept begins with integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s. An even number is an integer that is "evenly divisible" by 2, i.e., divisible by 2 without remainder; an odd number is an integer that is not evenly divisible by 2. (The old-fashioned term "evenly divisible" is now almost always shortened to "divisible".) A formal definition of an even number is that it is an integer of the form n = 2k, where k is an integer; it can then be shown that an odd number is an integer of the form n = 2k + 1.
Examples of even numbers are −4, 8, and 1728. Examples of odd numbers are −5, 9, 3, and 71. This classification only applies to integers, i.e., a fractional number like 1/2 or 4.201 is neither even nor odd.
The sets of even and odd numbers can be defined as following:
- Even =
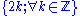
- Odd =
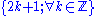
A number (i.e., integer) expressed in the decimal
Decimal
The decimal numeral system has ten as its base. It is the numerical base most widely used by modern civilizations....
numeral system
Numeral system
A numeral system is a writing system for expressing numbers, that is a mathematical notation for representing numbers of a given set, using graphemes or symbols in a consistent manner....
is even or odd according to whether its last digit is even or odd.
That is, if the last digit is 1, 3, 5, 7, or 9, then it's odd; otherwise it's even. The same idea will work using any even base.
In particular, a number expressed in the binary numeral system
Binary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
is odd if its last digit is 1 and even if its last digit is 0.
In an odd base, the number is even according to the sum of its digits – it is even if and only if the sum of its digits is even.
Arithmetic on even and odd numbers
The following laws can be verified using the properties of divisibility. They are a special case of rules in modular arithmeticModular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
, and are commonly used to check if an equality is likely to be correct by testing the parity of each side. As with ordinary arithmetic, multiplication and addition are commutative and associative, and multiplication is distributive over addition. However, subtraction in parity is identical to addition, so subtraction also possesses these properties (which are absent from ordinary arithmetic).
AdditionAdditionAddition is a mathematical operation that represents combining collections of objects together into a larger collection. It is signified by the plus sign . For example, in the picture on the right, there are 3 + 2 apples—meaning three apples and two other apples—which is the same as five apples....
and subtractionSubtractionIn arithmetic, subtraction is one of the four basic binary operations; it is the inverse of addition, meaning that if we start with any number and add any number and then subtract the same number we added, we return to the number we started with...
- odd ± even = odd;
Rules analogous to these for divisibility by 9 are used in the method of casting out nines
Casting out nines
Casting out nines is a sanity check to ensure that hand computations of sums, differences, products, and quotients of integers are correct. By looking at the digital roots of the inputs and outputs, the casting-out-nines method can help one check arithmetic calculations...
.
DivisionDivision (mathematics)right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
The division of two whole numbers does not necessarily result in a whole number.For example, 1 divided by 4 equals 1/4, which is neither even nor odd, since the concepts even and odd apply only to integers.
But when the quotient
Quotient
In mathematics, a quotient is the result of division. For example, when dividing 6 by 3, the quotient is 2, while 6 is called the dividend, and 3 the divisor. The quotient further is expressed as the number of times the divisor divides into the dividend e.g. The quotient of 6 and 2 is also 3.A...
is an integer, it will be even if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
the dividend
Division (mathematics)
right|thumb|200px|20 \div 4=5In mathematics, especially in elementary arithmetic, division is an arithmetic operation.Specifically, if c times b equals a, written:c \times b = a\,...
has more factors of two
Integer factorization
In number theory, integer factorization or prime factorization is the decomposition of a composite number into smaller non-trivial divisors, which when multiplied together equal the original integer....
than the divisor.
History
The ancient Greeks considered 1 to be neither fully odd nor fully even. Some of this sentiment survived into the 19th century: Friedrich Wilhelm August Fröbel's 1826 The Education of Man instructs the teacher to drill students with the claim that 1 is neither even nor odd, to which Fröbel attaches the philosophical afterthought,Music theory
In wind instrumentWind instrument
A wind instrument is a musical instrument that contains some type of resonator , in which a column of air is set into vibration by the player blowing into a mouthpiece set at the end of the resonator. The pitch of the vibration is determined by the length of the tube and by manual modifications of...
s with a cylindrical bore and in effect closed at one end, such as the clarinet
Clarinet
The clarinet is a musical instrument of woodwind type. The name derives from adding the suffix -et to the Italian word clarino , as the first clarinets had a strident tone similar to that of a trumpet. The instrument has an approximately cylindrical bore, and uses a single reed...
at the mouthpiece, the harmonic
Harmonic
A harmonic of a wave is a component frequency of the signal that is an integer multiple of the fundamental frequency, i.e. if the fundamental frequency is f, the harmonics have frequencies 2f, 3f, 4f, . . . etc. The harmonics have the property that they are all periodic at the fundamental...
s produced are odd multiples of the fundamental frequency
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...
. (With cylindrical pipes open at both ends, used for example in some organ stop
Organ stop
An organ stop is a component of a pipe organ that admits pressurized air to a set of organ pipes. Its name comes from the fact that stops can be used selectively by the organist; some can be "on" , while others can be "off" .The term can also refer...
s such as the open diapason, the harmonics are even multiples of the same frequency for the given bore length, but this has the effect of the fundamental frequency being doubled and all multiples of this fundamental frequency being produced.) See harmonic series (music)
Harmonic series (music)
Pitched musical instruments are often based on an approximate harmonic oscillator such as a string or a column of air, which oscillates at numerous frequencies simultaneously. At these resonant frequencies, waves travel in both directions along the string or air column, reinforcing and canceling...
.
Higher mathematics
The even numbers form an ideal in the ring of integers, but the odd numbers do not — this is clear from the fact that the identityIdentity (mathematics)
In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...
element for addition, zero, is an element of the even numbers only. An integer is even if it is congruent to 0 modulo
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
this ideal, in other words if it is congruent to 0 modulo 2, and odd if it is congruent to 1 modulo 2.
All prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
s are odd, with one exception: the prime number 2. All known perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s are even; it is unknown whether any odd perfect numbers exist.
The squares of all even numbers are even, and the squares of all odd numbers are odd. Since an even number can be expressed as 2x, (2x)2 = 4x2 which is even. Since an odd number can be expressed as 2x + 1, (2x + 1)2 = 4x2 + 4x + 1. 4x2 and 4x are even, which means that 4x2 + 4x + 1 is odd (since even + odd = odd).
Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
states that every even integer greater than 2 can be represented as a sum of two prime numbers.
Modern computer
Computer
A computer is a programmable machine designed to sequentially and automatically carry out a sequence of arithmetic or logical operations. The particular sequence of operations can be changed readily, allowing the computer to solve more than one kind of problem...
calculations have shown this conjecture to be true for integers up to at least 4 × 1014, but still no general proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
has been found.
The Feit–Thompson theorem states that a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
is always solvable if its order is an odd number. This is an example of odd numbers playing a role in an advanced mathematical theorem where the method of application of the simple hypothesis of "odd order" is far from obvious.
Parity for other objects

Parity is also used to refer to a number of other properties.
- The parity of a permutation (as defined in abstract algebraAbstract algebraAbstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
) is the parity of the number of transpositions into which the permutation can be decomposed. For example (ABC) to (BCA) is even because it can be done by swapping A and B then C and A (two transpositions). It can be shown that no permutation can be decomposed both in an even and in an odd number of transpositions. Hence the above is a suitable definition. In Rubik's CubeRubik's CubeRubik's Cube is a 3-D mechanical puzzle invented in 1974 by Hungarian sculptor and professor of architecture Ernő Rubik.Originally called the "Magic Cube", the puzzle was licensed by Rubik to be sold by Ideal Toy Corp. in 1980 and won the German Game of the Year special award for Best Puzzle that...
, MegaminxMegaminxThe Megaminx is a dodecahedron-shaped puzzle similar to the Rubik's Cube. It has a total of 50 movable pieces to rearrange, compared to the 20 movable pieces of the Rubik's cube.- History :...
, and other twisty puzzles, the moves of the puzzle allow only even permutations of the puzzle pieces, so parity is important in understanding the configuration spaceConfiguration space- Configuration space in physics :In classical mechanics, the configuration space is the space of possible positions that a physical system may attain, possibly subject to external constraints...
of these puzzles.
- The parity of a functionEven and odd functionsIn mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
describes how its values change when its arguments are exchanged with their negations. An even function, such as an even power of a variable, gives the same result for any argument as for its negation. An odd function, such as an odd power of a variable, gives for any argument the negation of its result when given the negation of that argument. It is possible for a function to be neither odd nor even, and for the case f(x) = 0, to be both odd and even.
- Integer coordinates of points in Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s of two or more dimensions also have a parity, usually defined as the parity of the sum of the coordinates. For instance, the checkerboard lattice contains all integer points of even parity. This feature manifests itself in chessChessChess is a two-player board game played on a chessboard, a square-checkered board with 64 squares arranged in an eight-by-eight grid. It is one of the world's most popular games, played by millions of people worldwide at home, in clubs, online, by correspondence, and in tournaments.Each player...
, as bishopBishopA bishop is an ordained or consecrated member of the Christian clergy who is generally entrusted with a position of authority and oversight. Within the Catholic Church, Eastern Orthodox, Oriental Orthodox Churches, in the Assyrian Church of the East, in the Independent Catholic Churches, and in the...
s are constrained to squares of the same parity; knights alternate parity between moves. This form of parity was famously used to solve the Mutilated chessboard problemMutilated chessboard problemThe mutilated chessboard problem is a tiling puzzle introduced by and discussed by Martin Gardner in his Scientific American column "Mathematical Games." The problem is as follows:...
.
See also
- Diagonal parity – RAID#Non-standard levels
- Even and odd functionsEven and odd functionsIn mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power series and Fourier series...
- Even and odd ordinalsEven and odd ordinalsIn mathematics, even and odd ordinals extend the concept of parity from the natural numbers to the ordinal numbers. They are useful in some transfinite induction proofs.The literature contains a few equivalent definitions of the parity of an ordinal α:...
- Even and odd permutationsEven and odd permutationsIn mathematics, when X is a finite set of at least two elements, the permutations of X fall into two classes of equal size: the even permutations and the odd permutations...
- Flight numberFlight numberA flight number, when combined with the name of the airline and the date, identifies a particular flight. This callsign should not be confused with the tail number of the aircraft, although both can be used as a call-sign as used in general aviation...
- House numberingHouse numberingHouse numbering is the system of giving a unique number to each building in a street or area, with the intention of making it easier to locate a particular building. The house number is often part of a postal address....
- Parity functionParity functionIn Boolean algebra, a parity function is a Boolean function whose value is 1 if the input vector has an odd number of ones.The parity function is notable for its role in theoretical investigation of circuit complexity of Boolean functions.-Definition:...
- Parity of zero
- Thue–Morse sequence
- United States numbered highwaysUnited States Numbered HighwaysThe system of United States Numbered Highways is an integrated system of roads and highways in the United States numbered within a nationwide grid...

