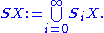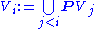In mathematical logic

Mathematical logic

Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...

, the universe of a structure

Structure (mathematical logic)

In universal algebra and in model theory, a structure consists of a set along with a collection of finitary operations and relations which are defined on it....

 (or model) is its domain

Domain of discourse

In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...

.

In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, and particularly in set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

 and the foundations of mathematics

Foundations of mathematics

Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...

, a universe is a class

Class (set theory)

In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...

 that contains (as elements) all the entities one wishes to consider in a given situation. There are several versions of this general idea, described in the following sections.

In a specific context

Perhaps the simplest version is that any set can be a universe, so long as the object of study is confined to that particular set.
If the object of study is formed by the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, then the real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

 R, which is the real number set, could be the universe under consideration.
Implicitly, this is the universe that Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

 was using when he first developed modern naive set theory

Naive set theory

Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...

 and cardinality in the 1870s and 1880s in applications to real analysis

Real analysis

Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...

.
The only sets that Cantor was originally interested in were subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s of R.

This concept of a universe is reflected in the use of Venn diagram

Venn diagram

Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...

s.
In a Venn diagram, the action traditionally takes place inside a large rectangle that represents the universe U.
One generally says that sets are represented by circles; but these sets can only be subsets of U.
The complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

 of a set A is then given by that portion of the rectangle outside of As circle.
Strictly speaking, this is the relative complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

 U \ A of A relative to U; but in a context where U is the universe, it can be regarded as the absolute complement

Complement (set theory)

In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...

 A^C of A.
Similarly, there is a notion of the nullary intersection, that is the intersection

Intersection (set theory)

In mathematics, the intersection of two sets A and B is the set that contains all elements of A that also belong to B , but no other elements....

 of zero

0 (number)

0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...

 sets (meaning no sets, not null set

Null set

In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...

s).
Without a universe, the nullary intersection would be the set of absolutely everything, which is generally regarded as impossible; but with the universe in mind, the nullary intersection can be treated as the set of everything under consideration, which is simply U.

These conventions are quite useful in the algebraic approach to basic set theory, based on Boolean lattices.
Except in some non-standard forms of axiomatic set theory (such as New Foundations

New Foundations

In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...

), the class

Class (set theory)

In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...

 of all sets is not a Boolean lattice (it is only a relatively complemented lattice).
In contrast, the class of all subsets of U, called the power set of U, is a Boolean lattice.
The absolute complement described above is the complement operation in the Boolean lattice; and U, as the nullary intersection, serves as the top element

Greatest element

In mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...

 (or nullary meet

Meet (mathematics)

In mathematics, join and meet are dual binary operations on the elements of a partially ordered set. A join on a set is defined as the supremum with respect to a partial order on the set, provided a supremum exists...

) in the Boolean lattice.
Then De Morgan's laws, which deal with complements of meets and joins (which are union

Union (set theory)

In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...

s in set theory) apply, and apply even to the nullary meet and the nullary join (which is the empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

).

In ordinary mathematics

However, once subsets of a given set X (in Cantor's case, X = R) are considered, the universe may need to be a set of subsets of X.
(For example, a topology

Topological space

Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...

 on X is a set of subsets of X.)
The various sets of subsets of X will not themselves be subsets of X but will instead be subsets of PX, the power set of X.
This may be continued; the object of study may next consist of such sets of subsets of X, and so on, in which case the universe will be P(PX).
In another direction, the binary relation

Binary relation

In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...

s on X (subsets of the Cartesian product

Cartesian product

In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...

  may be considered, or function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

s from X to itself, requiring universes like or X^X.

Thus, even if the primary interest is X, the universe may need to be considerably larger than X.
Following the above ideas, one may want the superstructure over X as the universe.
This can be defined by structural recursion as follows:

• Let S₀X be X itself.
• Let S₁X be the union
  Union (set theory)
  In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
  
   of X and PX.
• Let S₂X be the union of S₁X and P(S₁X).
• In general, let Sn+1X be the union of S_nX and P(SnX).

Then the superstructure over X, written SX, is the union of S₀X, S₁X, S₂X, and so on; or

Note that no matter what set X is the starting point, the empty set

Empty set

In mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...

 {} will belong to S₁X.
The empty set is the von Neumann ordinal [0].
Then {[0]}, the set whose only element is the empty set, will belong to S₂X; this is the von Neumann ordinal [1].
Similarly, {[1]} will belong to S₃X, and thus so will {[0],[1]}, as the union of {[0]} and {[1]}; this is the von Neumann ordinal [2].
Continuing this process, every natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

 is represented in the superstructure by its von Neumann ordinal.
Next, if x and y belong to the superstructure, then so does , which represents the ordered pair

Ordered pair

In mathematics, an ordered pair is a pair of mathematical objects. In the ordered pair , the object a is called the first entry, and the object b the second entry of the pair...

 (x,y).
Thus the superstructure will contain the various desired Cartesian products.
Then the superstructure also contains function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

s and relation

Relation (mathematics)

In set theory and logic, a relation is a property that assigns truth values to k-tuples of individuals. Typically, the property describes a possible connection between the components of a k-tuple...

s, since these may be represented as subsets of Cartesian products.
The process also gives ordered n-tuples, represented as functions whose domain is the von Neumann ordinal [n].
And so on.

So if the starting point is just X = {}, a great deal of the sets needed for mathematics appear as elements of the superstructure over {}.
But each of the elements of S{} will be finite sets!
Each of the natural numbers belongs to it, but the set N of all natural numbers does not (although it is a subset of S{}).
In fact, the superstructure over X consists of all of the hereditarily finite set

Hereditarily finite set

In mathematics and set theory, hereditarily finite sets are defined recursively as finite sets consisting of 0 or more hereditarily finite sets.-Formal definition:...

s.
As such, it can be considered the universe of finitist mathematics.
Speaking anachronistically, one could suggest that the 19th-century finitist Leopold Kronecker

Leopold Kronecker

Leopold Kronecker was a German mathematician who worked on number theory and algebra.He criticized Cantor's work on set theory, and was quoted by as having said, "God made integers; all else is the work of man"...

 was working in this universe; he believed that each natural number existed but that the set N (a "completed infinity") did not.

However, S{} is unsatisfactory for ordinary mathematicians (who are not finitists), because even though N may be available as a subset of S{}, still the power set of N is not.
In particular, arbitrary sets of real numbers are not available.
So it may be necessary to start the process all over again and form S(S{}).
However, to keep things simple, one can take the set N of natural numbers as given and form SN, the superstructure over N.
This is often considered the universe of ordinary mathematics

Ordinary mathematics

In the philosophy of mathematics, ordinary mathematics is an inexact term, used to distinguish the body of most mathematical work from that of, for example, constructivist, intuitionist, or finitist mathematics....

.
The idea is that all of the mathematics that is ordinarily studied refers to elements of this universe.
For example, any of the usual constructions of the real numbers (say by Dedekind cut

Dedekind cut

In mathematics, a Dedekind cut, named after Richard Dedekind, is a partition of the rationals into two non-empty parts A and B, such that all elements of A are less than all elements of B, and A contains no greatest element....

s) belongs to SN.
Even non-standard analysis

Non-standard analysis

Non-standard analysis is a branch of mathematics that formulates analysis using a rigorous notion of an infinitesimal number.Non-standard analysis was introduced in the early 1960s by the mathematician Abraham Robinson. He wrote:...

 can be done in the superstructure over a non-standard model

Non-standard model

In model theory, a discipline within mathematical logic, a non-standard model is a model of a theory that is not isomorphic to the intended model . If the intended model is infinite and the language is first-order, then the Löwenheim-Skolem theorems guarantee the existence of non-standard models...

 of the natural numbers.

One should note a slight shift in philosophy from the previous section, where the universe was any set U of interest.
There, the sets being studied were subsets of the universe; now, they are members of the universe.
Thus although P(SX) is a Boolean lattice, what is relevant is that SX itself is not.
Consequently, it is rare to apply the notions of Boolean lattices and Venn diagrams directly to the superstructure universe as they were to the power-set universes of the previous section.
Instead, one can work with the individual Boolean lattices PA, where A is any relevant set belonging to SX; then PA is a subset of SX (and in fact belongs to SX). In Cantor's case X = R in particular, arbitrary sets of real numbers are not available, so there it may indeed be necessary to start the process all over again.

In set theory

It is possible to give a precise meaning to the claim that SN is the universe of ordinary mathematics; it is a model

Model theory

In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....

 of Zermelo set theory

Zermelo set theory

Zermelo set theory, as set out in an important paper in 1908 by Ernst Zermelo, is the ancestor of modern set theory. It bears certain differences from its descendants, which are not always understood, and are frequently misquoted...

, the axiomatic set theory originally developed by Ernst Zermelo

Ernst Zermelo

Ernst Friedrich Ferdinand Zermelo was a German mathematician, whose work has major implications for the foundations of mathematics and hence on philosophy. He is known for his role in developing Zermelo–Fraenkel axiomatic set theory and his proof of the well-ordering theorem.-Life:He graduated...

 in 1908.
Zermelo set theory was successful precisely because it was capable of axiomatising "ordinary" mathematics, fulfilling the programme begun by Cantor over 30 years earlier.
But Zermelo set theory proved insufficient for the further development of axiomatic set theory and other work in the foundations of mathematics

Foundations of mathematics

Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...

, especially model theory

Model theory

In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....

.
For a dramatic example, the description of the superstructure process above cannot itself be carried out in Zermelo set theory!
The final step, forming S as an infinitary union, requires the axiom of replacement, which was added to Zermelo set theory in 1922 to form Zermelo-Fraenkel set theory, the set of axioms most widely accepted today.
So while ordinary mathematics may be done in SN, discussion of SN goes beyond the "ordinary", into metamathematics

Metamathematics

Metamathematics is the study of mathematics itself using mathematical methods. This study produces metatheories, which are mathematical theories about other mathematical theories...

.

But if high-powered set theory is brought in, the superstructure process above reveals itself to be merely the beginning of a transfinite recursion.
Going back to X = {}, the empty set, and introducing the (standard) notation Vi for Si{}, V₀ = {}, V₁ = P{}, and so on as before.
But what used to be called "superstructure" is now just the next item on the list: V_ω, where ω is the first infinite ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

.
This can be extended to arbitrary ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

s:

defines Vi for any ordinal number i.
The union of all of the Vi is the von Neumann universe

Von Neumann universe

In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted V, is the class of hereditary well-founded sets...

 V:

.

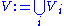Note that every individual Vi is a set, but their union V is a proper class.
The axiom of foundation, which was added to ZF set theory at around the same time as the axiom of replacement, says that every set belongs to V.

Kurt Gödel

Kurt Gödel

Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...

's constructible universe

Constructible universe

In mathematics, the constructible universe , denoted L, is a particular class of sets which can be described entirely in terms of simpler sets. It was introduced by Kurt Gödel in his 1938 paper "The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis"...

 L and the axiom of constructibility

Axiom of constructibility

The axiom of constructibility is a possible axiom for set theory in mathematics that asserts that every set is constructible. The axiom is usually written as V = L, where V and L denote the von Neumann universe and the constructible universe, respectively.- Implications :The axiom of...

Inaccessible cardinal

Inaccessible cardinal

In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...

s yield models of ZF and sometimes additional axioms, and are equivalent to the existence of the Grothendieck universe

Grothendieck universe

In mathematics, a Grothendieck universe is a set U with the following properties:# If x is an element of U and if y is an element of x, then y is also an element of U...

 set

In category theory

There is another approach to universes which is historically connected with category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

. This is the idea of a Grothendieck universe

Grothendieck universe

In mathematics, a Grothendieck universe is a set U with the following properties:# If x is an element of U and if y is an element of x, then y is also an element of U...

. Roughly speaking, a Grothendieck universe is a set inside which all the usual operations of set theory can be performed. For example, the union of any two sets in a Grothendieck universe U is still in U. Similarly, intersections, unordered pairs, power sets, and so on are also in U. This is similar to the idea of a superstructure above. The advantage of a Grothendieck universe is that it is actually a set, and never a proper class. The disadvantage is that if one tries hard enough, one can leave a Grothendieck universe.

The most common use of a Grothendieck universe U is to take U as a replacement for the category of all sets. One says that a set S is U-small if S ∈U, and U-large otherwise. The category U-Set of all U-small sets has as objects all U-small sets and as morphisms all functions between these sets. Both the object set and the morphism set are sets, so it becomes possible to discuss the category of "all" sets without invoking proper classes. Then it becomes possible to define other categories in terms of this new category. For example, the category of all U-small categories is the category of all categories whose object set and whose morphism set are in U. Then the usual arguments of set theory are applicable to the category of all categories, and one does not have to worry about accidentally talking about proper classes. Because Grothendieck universes are extremely large, this suffices in almost all applications.

Often when working with Grothendieck universes, mathematicians assume the Axiom of Universes: "For any set x, there exists a universe U such that x ∈U." The point of this axiom is that any set one encounters is then U-small for some U, so any argument done in a general Grothendieck universe can be applied. This axiom is closely related to the existence of strongly inaccessible cardinal

Inaccessible cardinal

In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...

s.

Set-like topos

Topos

In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...

es