
Successor ordinal
Encyclopedia
In set theory
, the successor of an ordinal number
α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal. Every ordinal other than 0 is either a successor ordinal or a limit ordinal.
Using von Neumann's ordinal numbers (the standard model of the ordinals used in set theory), the successor S(α) of an ordinal number α is given by the formula
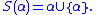
Since the ordering on the ordinal numbers α < β if and only if α ∈ β, it is immediate that there is no ordinal number between α and S(α), and it is also clear that α < S(α).
The successor operation can be used to define ordinal addition
rigorously via transfinite recursion
as follows:

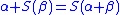
and for a limit ordinal λ
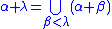
In particular, S(α) = α + 1. Multiplication and exponentiation are defined similarly.
The successor points and zero are the isolated point
s of the class of ordinal numbers, with respect to the order topology
.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the successor of an ordinal number
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal. Every ordinal other than 0 is either a successor ordinal or a limit ordinal.
Using von Neumann's ordinal numbers (the standard model of the ordinals used in set theory), the successor S(α) of an ordinal number α is given by the formula
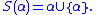
Since the ordering on the ordinal numbers α < β if and only if α ∈ β, it is immediate that there is no ordinal number between α and S(α), and it is also clear that α < S(α).
The successor operation can be used to define ordinal addition
Ordinal arithmetic
In the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
rigorously via transfinite recursion
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
as follows:

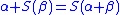
and for a limit ordinal λ
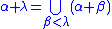
In particular, S(α) = α + 1. Multiplication and exponentiation are defined similarly.
The successor points and zero are the isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s of the class of ordinal numbers, with respect to the order topology
Order topology
In mathematics, an order topology is a certain topology that can be defined on any totally ordered set. It is a natural generalization of the topology of the real numbers to arbitrary totally ordered sets...
.
See also
- ordinal arithmeticOrdinal arithmeticIn the mathematical field of set theory, ordinal arithmetic describes the three usual operations on ordinal numbers: addition, multiplication, and exponentiation. Each can be defined in essentially two different ways: either by constructing an explicit well-ordered set which represents the...
- limit ordinal
- successor cardinalSuccessor cardinalIn the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...

