Mathematical beauty
Encyclopedia
.svg.png)
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s derive aesthetic
Aesthetics
Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste...
pleasure from their work, and from mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
in general. They express this pleasure by describing mathematics (or, at least, some aspect of mathematics) as beautiful. Sometimes mathematicians describe mathematics as an art
Art
Art is the product or process of deliberately arranging items in a way that influences and affects one or more of the senses, emotions, and intellect....
form or, at a minimum, as a creative activity. Comparisons are often made with music
Music
Music is an art form whose medium is sound and silence. Its common elements are pitch , rhythm , dynamics, and the sonic qualities of timbre and texture...
and poetry
Poetry
Poetry is a form of literary art in which language is used for its aesthetic and evocative qualities in addition to, or in lieu of, its apparent meaning...
.
Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
expressed his sense of mathematical beauty in these words:
Mathematics, rightly viewed, possesses not only truth, but supreme beauty — a beauty cold and austere, like that of sculptureSculptureSculpture is three-dimensional artwork created by shaping or combining hard materials—typically stone such as marble—or metal, glass, or wood. Softer materials can also be used, such as clay, textiles, plastics, polymers and softer metals...
, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show. The true spirit of delight, the exaltation, the sense of being more than Man, which is the touchstone of the highest excellence, is to be found in mathematics as surely as poetry.
Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
expressed his views on the ineffability
Ineffability
Ineffability is concerned with ideas that cannot or should not be expressed in spoken words , often being in the form of a taboo or incomprehensible term. This property is commonly associated with philosophy, aspects of existence, and similar concepts that are inherently "too great", complex, or...
of mathematics when he said, "Why are numbers beautiful? It's like asking why is Beethoven's Ninth Symphony
Symphony No. 9 (Beethoven)
The Symphony No. 9 in D minor, Op. 125, is the final complete symphony of Ludwig van Beethoven. Completed in 1824, the symphony is one of the best known works of the Western classical repertoire, and has been adapted for use as the European Anthem...
beautiful. If you don't see why, someone can't tell you. I know numbers are beautiful. If they aren't beautiful, nothing is."
Beauty in method
Mathematicians describe an especially pleasing method of proofMathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
as elegant
Elegance
Elegance is a synonym for beauty that has come to acquire the additional connotations of unusual effectiveness and simplicity. It is frequently used as a standard of tastefulness particularly in the areas of visual design, decoration, the sciences, and the esthetics of mathematics...
. Depending on context, this may mean:
- A proof that uses a minimum of additional assumptions or previous results.
- A proof that is unusually succinct.
- A proof that derives a result in a surprising way (e.g., from an apparently unrelated theorem or collection of theorems.)
- A proof that is based on new and original insights.
- A method of proof that can be easily generalized to solve a family of similar problems.
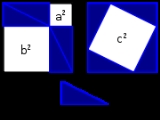
In the search for an elegant proof, mathematicians often look for different independent ways to prove a result—the first proof that is found may not be the best. The theorem for which the greatest number of different proofs have been discovered is possibly the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
, with hundreds of proofs having been published. Another theorem that has been proved in many different ways is the theorem of quadratic reciprocity
Quadratic reciprocity
In number theory, the law of quadratic reciprocity is a theorem about modular arithmetic which gives conditions for the solvability of quadratic equations modulo prime numbers...
—Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
alone published eight different proofs of this theorem.
Conversely, results that are logically correct but involve laborious calculations, over-elaborate methods, very conventional approaches, or that rely on a large number of particularly powerful axioms or previous results are not usually considered to be elegant, and may be called ugly or clumsy.
Beauty in results
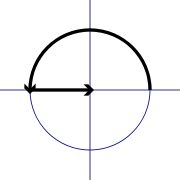
While it is difficult to find universal agreement on whether a result is deep, some examples are often cited. One is Euler's identity:
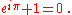
Physicist Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
called this "the most remarkable formula in mathematics". Modern examples include the modularity theorem, which establishes an important connection between elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s and modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s (work on which led to the awarding of the Wolf Prize to Andrew Wiles
Andrew Wiles
Sir Andrew John Wiles KBE FRS is a British mathematician and a Royal Society Research Professor at Oxford University, specializing in number theory...
and Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
), and "monstrous moonshine
Monstrous moonshine
In mathematics, monstrous moonshine, or moonshine theory, is a term devised by John Horton Conway and Simon P. Norton in 1979, used to describe the connection between the monster group M and modular functions .- History :Specifically, Conway and Norton, following an initial observationby John...
," which connects the Monster group
Monster group
In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
to modular functions via a string theory
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
for which Richard Borcherds
Richard Borcherds
Richard Ewen Borcherds is a British mathematician specializing in lattices, number theory, group theory, and infinite-dimensional algebras. He was awarded the Fields Medal in 1998.- Personal life :...
was awarded the Fields medal
Fields Medal
The Fields Medal, officially known as International Medal for Outstanding Discoveries in Mathematics, is a prize awarded to two, three, or four mathematicians not over 40 years of age at each International Congress of the International Mathematical Union , a meeting that takes place every four...
.
The opposite of deep is trivial. A trivial theorem may be a result that can be derived in an obvious and straightforward way from other known results, or which applies only to a specific set of particular objects such as the empty set. Sometimes, however, a statement of a theorem can be original enough to be considered deep, even though its proof is fairly obvious.
In his A Mathematician's Apology
A Mathematician's Apology
A Mathematician's Apology is a 1940 essay by British mathematician G. H. Hardy. It concerns the aesthetics of mathematics with some personal content, and gives the layman an insight into the mind of a working mathematician.-Summary:...
, Hardy
G. H. Hardy
Godfrey Harold “G. H.” Hardy FRS was a prominent English mathematician, known for his achievements in number theory and mathematical analysis....
suggests that a beautiful proof or result possesses "inevitability", "unexpectedness", and "economy".
Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, however, disagrees with unexpectedness as a condition for beauty and proposes a counterexample:
Perhaps ironically, Monastyrsky writes:
This disagreement illustrates both the subjective nature of mathematical beauty and its connection with mathematical results: in this case, not only the existence of exotic spheres, but also a particular realization of them.
Beauty in experience
Number
A number is a mathematical object used to count and measure. In mathematics, the definition of number has been extended over the years to include such numbers as zero, negative numbers, rational numbers, irrational numbers, and complex numbers....
s and symbol
Symbol
A symbol is something which represents an idea, a physical entity or a process but is distinct from it. The purpose of a symbol is to communicate meaning. For example, a red octagon may be a symbol for "STOP". On a map, a picture of a tent might represent a campsite. Numerals are symbols for...
s is probably required to engage in any mathematics. Given the utility of mathematics in science
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and engineering
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
, it is likely that any technological society will actively cultivate these aesthetics
Aesthetics
Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste...
, certainly in its philosophy of science
Philosophy of science
The philosophy of science is concerned with the assumptions, foundations, methods and implications of science. It is also concerned with the use and merit of science and sometimes overlaps metaphysics and epistemology by exploring whether scientific results are actually a study of truth...
if nowhere else.
The most intense experience of mathematical beauty for most mathematicians comes from actively engaging in mathematics. It is very difficult to enjoy or appreciate mathematics in a purely passive way—in mathematics there is no real analogy of the role of the spectator, audience, or viewer. Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
referred to the austere beauty of mathematics.
Beauty and philosophy
Some mathematicians are of the opinion that the doing of mathematics is closer to discovery than invention, for example:These mathematicians believe that the detailed and precise results of mathematics may be reasonably taken to be true without any dependence on the universe in which we live. For example, they would argue that the theory of the natural numbers is fundamentally valid, in a way that does not require any specific context. Some mathematicians have extrapolated this viewpoint that mathematical beauty is truth further, in some cases becoming mysticism
Mysticism
Mysticism is the knowledge of, and especially the personal experience of, states of consciousness, i.e. levels of being, beyond normal human perception, including experience and even communion with a supreme being.-Classical origins:...
.
Pythagoras
Pythagoras
Pythagoras of Samos was an Ionian Greek philosopher, mathematician, and founder of the religious movement called Pythagoreanism. Most of the information about Pythagoras was written down centuries after he lived, so very little reliable information is known about him...
(and his entire philosophical school, the Pythagoreans) believed in the literal reality of numbers. The discovery of the existence of irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
s was a shock to them—they considered the existence of numbers not expressible as the ratio of two natural numbers to be a flaw in nature. From the modern perspective, Pythagoras' mystical treatment of numbers was that of a numerologist rather than a mathematician. It turns out that what Pythagoras had missed in his world view was the limits of infinite sequences of ratios of natural numbers—the modern notion of a real number.
In Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
's philosophy there were two worlds, the physical one in which we live and another abstract world which contained unchanging truth, including mathematics. He believed that the physical world was a mere reflection of the more perfect abstract world.
Galileo Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
is reported to have said, "Mathematics is the language with which God wrote the universe."
Hungarian
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematician Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, although an atheist, spoke of an imaginary book, in which God has written down all the most beautiful mathematical proofs. When Erdős wanted to express particular appreciation of a proof, he would exclaim "This one's from The Book!" This viewpoint expresses the idea that mathematics, as the intrinsically true foundation on which the laws of our universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
are built, is a natural candidate for what has been personified as God
God
God is the English name given to a singular being in theistic and deistic religions who is either the sole deity in monotheism, or a single deity in polytheism....
by different religious mystics.
Twentieth-century French philosopher Alain Badiou
Alain Badiou
Alain Badiou is a French philosopher, professor at European Graduate School, formerly chair of Philosophy at the École Normale Supérieure . Along with Giorgio Agamben and Slavoj Žižek, Badiou is a prominent figure in an anti-postmodern strand of continental philosophy...
claims that ontology
Ontology
Ontology is the philosophical study of the nature of being, existence or reality as such, as well as the basic categories of being and their relations...
is mathematics. Badiou also believes in deep connections between mathematics, poetry and philosophy.
In some cases, natural philosophers and other scientists who have made extensive use of mathematics have made leaps of inference between beauty and physical truth in ways that turned out to be erroneous. For example, at one stage in his life, Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
believed that the proportions of the orbits of the then-known planets in the Solar System
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
have been arranged by God
God
God is the English name given to a singular being in theistic and deistic religions who is either the sole deity in monotheism, or a single deity in polytheism....
to correspond to a concentric arrangement of the five Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s, each orbit lying on the circumsphere of one polyhedron and the insphere of another. As there are exactly five Platonic solids, Kepler's hypothesis could only accommodate six planetary orbits and was disproved by the subsequent discovery of Uranus
Uranus
Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus...
.
Beauty and mathematical information theory
In the 1970s, Abraham MolesAbraham Moles
Abraham Moles was an engineer of electrical engineering and acoustics, and a doctor of physics and philosophy. He was one of the first researchers to establish and analyze links between aesthetics and information theory....
and Frieder Nake
Frieder Nake
Frieder Nake is a professor for computer graphics at the department for computer science at the University of Bremen and visiting professor for hypermedia design at the University of the Arts Bremen. He lives and works in Bremen, Germany.He has taught in Stuttgart, Toronto and Vancouver, and has...
analyzed links between beauty, information processing
Information processing
Information processing is the change of information in any manner detectable by an observer. As such, it is a process which describes everything which happens in the universe, from the falling of a rock to the printing of a text file from a digital computer system...
, and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. In the 1990s, Jürgen Schmidhuber
Jürgen Schmidhuber
Jürgen Schmidhuber is a computer scientist and artist known for his work on machine learning, universal Artificial Intelligence , artificial neural networks, digital physics, and low-complexity art. His contributions also include generalizations of Kolmogorov complexity and the Speed Prior...
formulated a mathematical theory of observer-dependent subjective beauty based on algorithmic information theory
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
: the most beautiful objects among subjectively comparable objects have short algorithmic descriptions (i.e., Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
) relative to what the observer already knows. Schmidhuber explicitly distinguishes between beautiful and interesting. The latter corresponds to the first derivative of subjectively perceived beauty:
the observer continually tries to improve the predictability
Predictability
Predictability is the degree to which a correct prediction or forecast of a system's state can be made either qualitatively or quantitatively.-Predictability and Causality:...
and compressibility of the observations by discovering regularities such as repetitions and symmetries and fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
self-similarity
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
. Whenever the observer's learning process (possibly a predictive artificial neural network
Neural network
The term neural network was traditionally used to refer to a network or circuit of biological neurons. The modern usage of the term often refers to artificial neural networks, which are composed of artificial neurons or nodes...
) leads to improved data compression such that the observation sequence can be described by fewer bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s than before, the temporary interestingness of the data corresponds to the compression progress, and is proportional to the observer's internal curiosity reward
Mathematics and art
The psychologyPsychology
Psychology is the study of the mind and behavior. Its immediate goal is to understand individuals and groups by both establishing general principles and researching specific cases. For many, the ultimate goal of psychology is to benefit society...
of the aesthetics
Aesthetics
Aesthetics is a branch of philosophy dealing with the nature of beauty, art, and taste, and with the creation and appreciation of beauty. It is more scientifically defined as the study of sensory or sensori-emotional values, sometimes called judgments of sentiment and taste...
of mathematics is studied post-psychoanalytic
Psychoanalysis
Psychoanalysis is a psychological theory developed in the late 19th and early 20th centuries by Austrian neurologist Sigmund Freud. Psychoanalysis has expanded, been criticized and developed in different directions, mostly by some of Freud's former students, such as Alfred Adler and Carl Gustav...
ally in psychosynthesis
Psychosynthesis
Psychosynthesis is an approach to psychology that was developed by Roberto Assagioli, M.D. He compared psychosynthesis to the prevailing thinking of the day, contrasting psychosynthesis for example with Existential psychology, but unlike the latter considered loneliness not to be "either ultimate...
(in the work of Piero Ferrucci
Piero Ferrucci
Piero Ferrucci is a psychotherapist and a philosopher. He graduated from the University of Torino in 1970. He was trained by Roberto Assagioli, the founder of psychosynthesis, and has written several books:...
), in cognitive psychology
Cognitive psychology
Cognitive psychology is a subdiscipline of psychology exploring internal mental processes.It is the study of how people perceive, remember, think, speak, and solve problems.Cognitive psychology differs from previous psychological approaches in two key ways....
(in illusion
Illusion
An illusion is a distortion of the senses, revealing how the brain normally organizes and interprets sensory stimulation. While illusions distort reality, they are generally shared by most people....
studies using self-similarity
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
in Shepard tone
Shepard tone
A Shepard tone, named after Roger Shepard, is a sound consisting of a superposition of sine waves separated by octaves. When played with the base pitch of the tone moving upward or downward, it is referred to as the Shepard scale. This creates the auditory illusion of a tone that continually...
s), and the neuropsychology
Neuropsychology
Neuropsychology studies the structure and function of the brain related to specific psychological processes and behaviors. The term neuropsychology has been applied to lesion studies in humans and animals. It has also been applied to efforts to record electrical activity from individual cells in...
of aesthetic appreciation. Examples of the use of mathematics in the arts include:
- Music – the Stochastic music of Iannis XenakisIannis XenakisIannis Xenakis was a Romanian-born Greek ethnic, naturalized French composer, music theorist, and architect-engineer. He is commonly recognized as one of the most important post-war avant-garde composers...
, counterpointCounterpointIn music, counterpoint is the relationship between two or more voices that are independent in contour and rhythm and are harmonically interdependent . It has been most commonly identified in classical music, developing strongly during the Renaissance and in much of the common practice period,...
of Johann Sebastian BachJohann Sebastian BachJohann Sebastian Bach was a German composer, organist, harpsichordist, violist, and violinist whose sacred and secular works for choir, orchestra, and solo instruments drew together the strands of the Baroque period and brought it to its ultimate maturity...
, polyrhythmPolyrhythmPolyrhythm is the simultaneous sounding of two or more independent rhythms.Polyrhythm in general is a nonspecific term for the simultaneous occurrence of two or more conflicting rhythms, of which cross-rhythm is a specific and definable subset.—Novotney Polyrhythms can be distinguished from...
ic structureStructureStructure is a fundamental, tangible or intangible notion referring to the recognition, observation, nature, and permanence of patterns and relationships of entities. This notion may itself be an object, such as a built structure, or an attribute, such as the structure of society...
s (as in Igor StravinskyIgor StravinskyIgor Fyodorovich Stravinsky ; 6 April 1971) was a Russian, later naturalized French, and then naturalized American composer, pianist, and conductor....
's The Rite of SpringThe Rite of SpringThe Rite of Spring, original French title Le sacre du printemps , is a ballet with music by Igor Stravinsky; choreography by Vaslav Nijinsky; and concept, set design and costumes by Nicholas Roerich...
), the Metric modulationMetric modulationIn music a metric modulation is a change from one time signature/tempo to another, wherein a note value from the first is made equivalent to a note value in the second, like a pivot...
of Elliott CarterElliott CarterElliott Cook Carter, Jr. is a two-time Pulitzer Prize-winning American composer born and living in New York City. He studied with Nadia Boulanger in Paris in the 1930s, and then returned to the United States. After a neoclassical phase, he went on to write atonal, rhythmically complex music...
, permutationPermutationIn mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
theory in serialismSerialismIn music, serialism is a method or technique of composition that uses a series of values to manipulate different musical elements. Serialism began primarily with Arnold Schoenberg's twelve-tone technique, though his contemporaries were also working to establish serialism as one example of...
beginning with Arnold SchoenbergArnold SchoenbergArnold Schoenberg was an Austrian composer, associated with the expressionist movement in German poetry and art, and leader of the Second Viennese School...
, and application of Shepard tones in Karlheinz StockhausenKarlheinz StockhausenKarlheinz Stockhausen was a German composer, widely acknowledged by critics as one of the most important but also controversial composers of the 20th and early 21st centuries. Another critic calls him "one of the great visionaries of 20th-century music"...
s HymnenHymnenHymnen is an electronic and concrete work, with optional live performers, by Karlheinz Stockhausen, composed in 1966–67, and elaborated in 1969. In the composer's catalog of works, it is "Nr. 22".-Musical form and content:...
. - Choreography – shuffling has been applied to choreographyChoreographyChoreography is the art of designing sequences of movements in which motion, form, or both are specified. Choreography may also refer to the design itself, which is sometimes expressed by means of dance notation. The word choreography literally means "dance-writing" from the Greek words "χορεία" ...
as in the Temple of Rudra operaOperaOpera is an art form in which singers and musicians perform a dramatic work combining text and musical score, usually in a theatrical setting. Opera incorporates many of the elements of spoken theatre, such as acting, scenery, and costumes and sometimes includes dance...
. - Visual arts – examples include applications of chaos theoryChaos theoryChaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
and fractalFractalA fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
geometryGeometryGeometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
to computer-generated artDigital artDigital art is a general term for a range of artistic works and practices that use digital technology as an essential part of the creative and/or presentation process...
, symmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
studies of Leonardo da VinciLeonardo da VinciLeonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
, projective geometriesProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
in development of the perspectivePerspective (graphical)Perspective in the graphic arts, such as drawing, is an approximate representation, on a flat surface , of an image as it is seen by the eye...
theory of RenaissanceRenaissanceThe Renaissance was a cultural movement that spanned roughly the 14th to the 17th century, beginning in Italy in the Late Middle Ages and later spreading to the rest of Europe. The term is also used more loosely to refer to the historical era, but since the changes of the Renaissance were not...
art, grids in Op artOp artOp art, also known as optical art, is a style of visual art that makes use of optical illusions."Optical art is a method of painting concerning the interaction between illusion and picture plane, between understanding and seeing." Op art works are abstract, with many of the better known pieces made...
, optical geometry in the camera obscuraCamera obscuraThe camera obscura is an optical device that projects an image of its surroundings on a screen. It is used in drawing and for entertainment, and was one of the inventions that led to photography. The device consists of a box or room with a hole in one side...
of Giambattista della PortaGiambattista della PortaGiambattista della Porta , also known as Giovanni Battista Della Porta and John Baptist Porta, was an Italian scholar, polymath and playwright who lived in Naples at the time of the Scientific Revolution and Reformation....
, and multiple perspective in analytic cubismCubismCubism was a 20th century avant-garde art movement, pioneered by Pablo Picasso and Georges Braque, that revolutionized European painting and sculpture, and inspired related movements in music, literature and architecture...
and futurismFuturismFuturism was an artistic and social movement that originated in Italy in the early 20th century.Futurism or futurist may refer to:* Afrofuturism, an African-American and African diaspora subculture* Cubo-Futurism* Ego-Futurism...
.
The symmetries of two dimensional tesselations and three dimensional mathematical objects, can evoke feelings of "mathematical beauty" as expressed by Bertrand Russell
Bertrand Russell
Bertrand Arthur William Russell, 3rd Earl Russell, OM, FRS was a British philosopher, logician, mathematician, historian, and social critic. At various points in his life he considered himself a liberal, a socialist, and a pacifist, but he also admitted that he had never been any of these things...
in the first paragraphs of this article. This may apply to polyhedrons (three dimensional geometric solids), many of which show perfect symmetries that, combined with the use of colours, result in a visual experience that many consider attractive. The use in art of such objects or tesselations is limited though, as this beauty is often considered soulless and does not evoke feelings of emotion. The Dutch graphic designer M.C. Escher created mathematically inspired woodcuts, lithographs, and mezzotints. These feature impossible constructions, explorations of infinity, architecture, visual paradoxes and tessellations. Currently, also computer generated art is based on mathematical algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s.
External links
- Is Mathematics Beautiful?
- Links Concerning Beauty and Mathematics
- Mathematics and Beauty
- The Beauty of Mathematics
- Justin Mullins
- Edna St. Vincent Millay (poet): Euclid alone has looked on beauty bare
- The method for transformation of music into an image through numbers and geometrical proportions
- Terence TaoTerence TaoTerence Chi-Shen Tao FRS is an Australian mathematician working primarily on harmonic analysis, partial differential equations, combinatorics, analytic number theory and representation theory...
, What is good mathematics?

