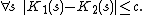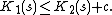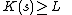
Kolmogorov complexity
Encyclopedia
In algorithmic information theory
(a subfield of computer science
), the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computation
al resources needed to specify the object. It is named after Soviet Russian mathematician Andrey Kolmogorov
.
Kolmogorov complexity is also known as descriptive complexityNot to be confused with descriptive complexity theory, analysis of the complexity of decision problems by their expressibility as logical formulae., Kolmogorov–Chaitin
complexity, algorithmic entropy, or program-size complexity.
For example, consider the following two strings
of length 64, each containing only lowercase letters, digits, and spaces:
The first string has a short English-language description, namely "ab 32 times", which consists of 11 characters. The second one has no obvious simple description (using the same character set) other than writing down the string itself, which has 64 characters.
More formally, the complexity
of a string is the length of the string's shortest description in some fixed universal description language
. The sensitivity of complexity relative to the choice of description language is discussed below. It can be shown that the Kolmogorov complexity of any string cannot be more than a few bytes larger than the length of the string itself. Strings whose Kolmogorov complexity is small relative to the string's size are not considered to be complex.
The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Gödel's incompleteness theorem and Turing's halting problem
.
, Pascal
, or Java Virtual Machine
bytecode. If P is a program which outputs a string x, then P is a description of x. The length of the description is just the length of P as a character string. In determining the length of P, the lengths of any subroutines used in P must be accounted for. The length of any integer constant n which occurs in the program P is the number of bits required to represent n, that is (roughly) log2n.
We could alternatively choose an encoding for Turing machine
s, where an encoding is a function which associates to each Turing Machine M a bitstring <M>. If M is a Turing Machine which on input w outputs string x, then the concatenated string <M> w is a description of x. For theoretical analysis, this approach is more suited for constructing detailed formal proofs and is generally preferred in the research literature. The binary lambda calculus
may provide the simplest definition of complexity yet. In this article we will use an informal approach.
Any string s has at least one description, namely the program
function GenerateFixedString
return s
If a description of s, d(s), is of minimal length—i.e. it uses the fewest number of characters—it is called a minimal description of s. Then the length of d(s)—i.e. the number of characters in the description—is the Kolmogorov complexity of s, written K(s). Symbolically,
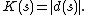
We now consider how the choice of description language affects the value of K and show that the effect of changing the description language is bounded.
Theorem. If K1 and K2 are the complexity functions relative to description languages L1 and L2, then there is a constant c (which depends only on the languages L1 and L2) such that
Proof. By symmetry, it suffices to prove that there is some constant c such that for all bitstrings s,
Now, suppose there is a program in the language L1 which acts as an interpreter
for L2:
function InterpretLanguage(string p)
where p is a program in L2. The interpreter is characterized by the following property:
Thus if P is a program in L2 which is a minimal description of s, then InterpretLanguage(P) returns the string s. The length of this description of s is the sum of
This proves the desired upper bound.
See also invariance theorem
.
is the area of computer science that studies Kolmogorov complexity and other complexity measures on strings (or other data structure
s).
The concept and theory of Kolmogorov Complexity is based on a crucial theorem first discovered by Ray Solomonoff
who published it in 1960, describing it in "A Preliminary Report on a General Theory of Inductive Inference" as part of his invention of algorithmic probability
. He gave a more complete description in his 1964 publications, "A Formal Theory of Inductive Inference," Part 1 and Part 2 in Information and Control.
Andrey Kolmogorov
later independently published
this theorem in Problems Inform. Transmission, Gregory Chaitin
also presents this theorem in J. ACM; Chaitin's paper was submitted October 1966, revised in December 1968 and cites both Solomonoff's and Kolmogorov's papers.
The theorem says that among algorithms that decode strings from their descriptions (codes) there exists an optimal one. This algorithm, for all strings, allows codes as short as allowed by any other algorithm up to an additive constant that depends on the algorithms, but not on the strings themselves. Solomonoff used this algorithm, and the code lengths it allows, to define a string's `universal probability' on which inductive inference of a string's subsequent digits can be based. Kolmogorov used this theorem to define several functions of strings: complexity, randomness, and information.
When Kolmogorov became aware of Solomonoff's work, he acknowledged Solomonoff's priority For several years, Solomonoff's work was better known in the Soviet Union than in the Western World. The general consensus in the scientific community, however, was to associate this type of complexity with Kolmogorov, who was concerned with randomness of a sequence while Algorithmic Probability became associated with Solomonoff, who focused on prediction using his invention of the universal a priori probability distribution.
There are several other variants of Kolmogorov complexity or algorithmic information. The most widely used one is based on self-delimiting programs and is mainly due to Leonid Levin
(1974).
An axiomatic approach to Kolmogorov complexity based on Blum axioms
(Blum 1967) was introduced by Mark Burgin in the paper presented for publication by Andrey Kolmogorov
(Burgin 1982).
Some consider that naming the concept "Kolmogorov complexity" is an example of the Matthew effect
.
It is not hard to see that the minimal description of a string cannot be too much larger than the string itself: the program GenerateFixedString above that outputs s is a fixed amount larger than s.
Theorem. There is a constant c such that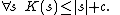
Theorem. K is not a computable function
.
In other words, there is no program which takes a string s as input and produces the integer K(s) as output. We show this by contradiction by making a program that creates a string that should only be able to be created by a longer program. Suppose there is a program
function KolmogorovComplexity(string s)
that takes as input a string s and returns K(s). Now consider the program
function GenerateComplexString(int n)
for i = 1 to infinity:
for each string s of length exactly i
if KolmogorovComplexity(s) >= n
return s
quit
This program calls KolmogorovComplexity as a subroutine. This program tries every string, starting with the shortest, until it finds a string with complexity at least n, then returns that string. Therefore, given any positive integer n, it produces a string with Kolmogorov complexity at least as great as n. The program itself has a fixed length U. The input to the program GenerateComplexString is an integer n; here, the size of n is measured by the number of bits required to represent n which is log2(n). Now consider the following program:
function GenerateParadoxicalString
return GenerateComplexString(n0)
This program calls GenerateComplexString as a subroutine and also has a free parameter
n0. This program outputs a string s whose complexity is at least n0. By an auspicious choice of the parameter n0 we will arrive at a contradiction. To choose this value, note s is described by the program GenerateParadoxicalString whose length is at most
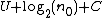
where C is the "overhead" added by the program GenerateParadoxicalString. Since n grows faster than log2(n), there exists a value n0 such that
But this contradicts the definition of s having a complexity at least n0. That is, by the definition of K(s), the string s returned by GenerateParadoxicalString is only supposed to be able to be generated by a program of length n0 or longer, but GenerateParadoxicalString is shorter than n0. Thus the program named "KolmogorovComplexity" cannot actually computably find the complexity of arbitrary strings.
This is proof by contradiction where the contradiction is similar to the Berry paradox
: "Let n be the smallest positive integer that cannot be defined in fewer than twenty English words." It is also possible to show the uncomputability of K by reduction from the uncomputability of the halting problem
H, since K and H are Turing-equivalent
.http://www.daimi.au.dk/~bromille/DC05/Kolmogorov.pdf
In the programming languages community there is a corollary known as the full employment theorem
, stating there is no perfect size-optimizing compiler.
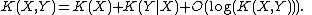
It states that the shortest program that reproduces X and Y is no more than a logarithmic term larger than a program to reproduce X and a program to reproduce Y given X. Using this statement one can define an analogue of mutual information for Kolmogorov complexity.
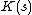 : simply compress
: simply compress
the string with some method, implement the corresponding decompressor in the chosen language, concatenate the decompressor to the compressed string, and measure the resulting string's length.
with some method, implement the corresponding decompressor in the chosen language, concatenate the decompressor to the compressed string, and measure the resulting string's length.
A string s is compressible by a number c if it has a description whose length does not exceed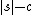 . This is equivalent to saying
. This is equivalent to saying  . Otherwise s is incompressible by c. A string incompressible by 1 is said to be simply incompressible; by the pigeonhole principle which applies because every compressed string maps to only one uncompressed string, incompressible string
. Otherwise s is incompressible by c. A string incompressible by 1 is said to be simply incompressible; by the pigeonhole principle which applies because every compressed string maps to only one uncompressed string, incompressible string
s must exist, since there are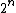 bit strings of length n but only 2n − 1 shorter strings, that is strings of length less than n, i.e. with length 0,1,...,n-1.
bit strings of length n but only 2n − 1 shorter strings, that is strings of length less than n, i.e. with length 0,1,...,n-1.
For the same reason, most strings are complex in the sense that they cannot be significantly compressed: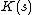 is not much smaller than
is not much smaller than 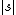 , the length of s in bits. To make this precise, fix a value of n. There are
, the length of s in bits. To make this precise, fix a value of n. There are 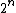 bitstrings of length n. The uniform probability
bitstrings of length n. The uniform probability
distribution on the space of these bitstrings assigns exactly equal weight to each string of length n.
to each string of length n.
Theorem. With the uniform probability distribution on the space of bitstrings of length n, the probability that a string is incompressible by c is at least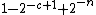 .
.
To prove the theorem, note that the number of descriptions of length not exceeding is given by the geometric series:
is given by the geometric series:
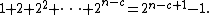
There remain at least
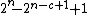
many bitstrings of length n that are incompressible by c. To determine the probability divide by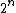 .
.
S for the natural number
s. The axiomatic system has to be powerful enough so that to certain assertions A about complexity of strings one can associate a formula FA in S. This association must have the following property: if FA is provable from the axioms of S, then the corresponding assertion A is true. This "formalization" can be achieved either by an artificial encoding such as a Gödel numbering or by a formalization which more clearly respects the intended interpretation of S.
Theorem. There exists a constant L (which only depends on the particular axiomatic system and the choice of description language) such that there does not exist a string s for which the statement
(as formalized in S) can be proven within the axiomatic system S.
Note that by the abundance of nearly incompressible strings, the vast majority of those statements must be true.
The proof of this result is modeled on a self-referential construction used in Berry's paradox. The proof is by contradiction. If the theorem were false, then
We can find an effective enumeration of all the formal proofs in S by some procedure
function NthProof(int n)
which takes as input n and outputs some proof. This function
enumerates all proofs. Some of these are proofs for formulas we do not
care about here (examples of proofs which will be listed by the procedure NthProof are the various known proofs of the law of quadratic reciprocity, those of Fermat's little theorem
or the proof of Fermat's last theorem
all translated into the formal language of S). Some of these are complexity formulas of the form K(s) ≥ n where s and n are constants in the language of S. There is a program
function NthProofProvesComplexityFormula(int n)
which determines whether the nth proof actually proves
a complexity formula K(s) ≥ L. The strings s and
the integer L in turn are computable by programs:
function StringNthProof(int n)
function ComplexityLowerBoundNthProof(int n)
Consider the following program
function GenerateProvablyComplexString(int n)
for i = 1 to infinity:
if NthProofProvesComplexityFormula(i) and ComplexityLowerBoundNthProof(i) ≥ n
return StringNthProof(i)
quit
Given an n, this program tries every proof until it finds a string
and a proof in the formal system
S of the formula K(s) ≥ L for some L ≥ n. The program
terminates by our Assumption (X). Now this program has a length U.
There is an integer n0 such that U + log2(n0) + C < n0, where C is the overhead cost of
function GenerateProvablyParadoxicalString
return GenerateProvablyComplexString(n0)
quit
The program GenerateProvablyParadoxicalString outputs a string s for which there exists an L such that K(s) ≥ L can be formally proved in S with L ≥ n0. In particular K(s) ≥
n0 is true. However, s is also described by a program of length
U + log2(n0) + C so its complexity is less than n0. This contradiction proves Assumption (X) cannot hold.
Similar ideas are used to prove the properties of Chaitin's constant
.
principle of statistical and inductive inference and machine learning was developed by C.S. Wallace
and D.M. Boulton in 1968. MML is Bayesian
(it incorporates prior beliefs) and
information-theoretic. It has the desirable properties of statistical
invariance (the inference transforms with a re-parametrisation, such as from
polar coordinates to Cartesian coordinates), statistical consistency (even
for very hard problems, MML will converge to any underlying model) and efficiency (the MML model will converge to any true underlying model about as quickly as is possible). C.S. Wallace and D.L. Dowe (1999) showed a formal connection between MML and algorithmic information theory (or Kolmogorov complexity).
Kolmogorov randomness (also called algorithmic randomness) defines a string
(usually of bit
s) as being random
if and only if it is shorter than any computer program
that can produce that string. This definition of randomness is critically dependent on the definition of Kolmogorov complexity. To make this definition complete, a computer has to be specified, usually a Turing machine
. According to the above definition of randomness, a random string is also an "incompressible" string, in the sense that it is impossible to give a representation of the string using a program whose length is shorter than the length of the string itself. However, according to this definition, most strings shorter than a certain length end up being (Chaitin-Kolmogorovically) random because the best one can do with very small strings is to write a program that simply prints these strings.
Algorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
(a subfield of computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
), the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computation
Computation
Computation is defined as any type of calculation. Also defined as use of computer technology in Information processing.Computation is a process following a well-defined model understood and expressed in an algorithm, protocol, network topology, etc...
al resources needed to specify the object. It is named after Soviet Russian mathematician Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
.
Kolmogorov complexity is also known as descriptive complexityNot to be confused with descriptive complexity theory, analysis of the complexity of decision problems by their expressibility as logical formulae., Kolmogorov–Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
complexity, algorithmic entropy, or program-size complexity.
For example, consider the following two strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
of length 64, each containing only lowercase letters, digits, and spaces:
abababababababababababababababababababababababababababababababab
4c1j5b2p0cv4w1x8rx2y39umgw5q85s7uraquuxdppa0q7nieieqe9noc4cvafzf
The first string has a short English-language description, namely "ab 32 times", which consists of 11 characters. The second one has no obvious simple description (using the same character set) other than writing down the string itself, which has 64 characters.
More formally, the complexity
Complexity
In general usage, complexity tends to be used to characterize something with many parts in intricate arrangement. The study of these complex linkages is the main goal of complex systems theory. In science there are at this time a number of approaches to characterizing complexity, many of which are...
of a string is the length of the string's shortest description in some fixed universal description language
Description language
Description language may refer to:* Interface description language aka interface definition language ** Regular Language description for XML ** Web Services Description Language ** Page description language...
. The sensitivity of complexity relative to the choice of description language is discussed below. It can be shown that the Kolmogorov complexity of any string cannot be more than a few bytes larger than the length of the string itself. Strings whose Kolmogorov complexity is small relative to the string's size are not considered to be complex.
The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Gödel's incompleteness theorem and Turing's halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
.
Definition
To define Kolmogorov complexity, we must first specify a description language for strings. Such a description language can be based on any programming language, such as LispLisp programming language
Lisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
, Pascal
Pascal (programming language)
Pascal is an influential imperative and procedural programming language, designed in 1968/9 and published in 1970 by Niklaus Wirth as a small and efficient language intended to encourage good programming practices using structured programming and data structuring.A derivative known as Object Pascal...
, or Java Virtual Machine
Java Virtual Machine
A Java virtual machine is a virtual machine capable of executing Java bytecode. It is the code execution component of the Java software platform. Sun Microsystems stated that there are over 4.5 billion JVM-enabled devices.-Overview:...
bytecode. If P is a program which outputs a string x, then P is a description of x. The length of the description is just the length of P as a character string. In determining the length of P, the lengths of any subroutines used in P must be accounted for. The length of any integer constant n which occurs in the program P is the number of bits required to represent n, that is (roughly) log2n.
We could alternatively choose an encoding for Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s, where an encoding is a function which associates to each Turing Machine M a bitstring <M>. If M is a Turing Machine which on input w outputs string x, then the concatenated string <M> w is a description of x. For theoretical analysis, this approach is more suited for constructing detailed formal proofs and is generally preferred in the research literature. The binary lambda calculus
Binary lambda calculus
Binary lambda calculus is a technique for using the lambda calculus to study Kolmogorov complexity, by working with a standard binary encoding of lambda terms, and a designated universal machine...
may provide the simplest definition of complexity yet. In this article we will use an informal approach.
Any string s has at least one description, namely the program
function GenerateFixedString
return s
If a description of s, d(s), is of minimal length—i.e. it uses the fewest number of characters—it is called a minimal description of s. Then the length of d(s)—i.e. the number of characters in the description—is the Kolmogorov complexity of s, written K(s). Symbolically,
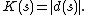
We now consider how the choice of description language affects the value of K and show that the effect of changing the description language is bounded.
Theorem. If K1 and K2 are the complexity functions relative to description languages L1 and L2, then there is a constant c (which depends only on the languages L1 and L2) such that
Proof. By symmetry, it suffices to prove that there is some constant c such that for all bitstrings s,
Now, suppose there is a program in the language L1 which acts as an interpreter
Interpreter (computing)
In computer science, an interpreter normally means a computer program that executes, i.e. performs, instructions written in a programming language...
for L2:
function InterpretLanguage(string p)
where p is a program in L2. The interpreter is characterized by the following property:
- Running InterpretLanguage on input p returns the result of running p.
Thus if P is a program in L2 which is a minimal description of s, then InterpretLanguage(P) returns the string s. The length of this description of s is the sum of
- The length of the program InterpretLanguage, which we can take to be the constant c.
- The length of P which by definition is K2(s).
This proves the desired upper bound.
See also invariance theorem
Invariance theorem
In algorithmic information theory, the invariance theorem, originally proved by Ray Solomonoff, states that a universal Turing machine provides an optimal means of description, up to an additive constant...
.
History and context
Algorithmic information theoryAlgorithmic information theory
Algorithmic information theory is a subfield of information theory and computer science that concerns itself with the relationship between computation and information...
is the area of computer science that studies Kolmogorov complexity and other complexity measures on strings (or other data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s).
The concept and theory of Kolmogorov Complexity is based on a crucial theorem first discovered by Ray Solomonoff
Ray Solomonoff
Ray Solomonoff was the inventor of algorithmic probability, and founder of algorithmic information theory, He was an originator of the branch of artificial intelligence based on machine learning, prediction and probability...
who published it in 1960, describing it in "A Preliminary Report on a General Theory of Inductive Inference" as part of his invention of algorithmic probability
Algorithmic probability
In algorithmic information theory, algorithmic probability is a method of assigning a probability to each hypothesis that explains a given observation, with the simplest hypothesis having the highest probability and the increasingly complex hypotheses receiving increasingly small probabilities...
. He gave a more complete description in his 1964 publications, "A Formal Theory of Inductive Inference," Part 1 and Part 2 in Information and Control.
Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
later independently published
Multiple discovery
The concept of multiple discovery is the hypothesis that most scientific discoveries and inventions are made independently and more or less simultaneously by multiple scientists and inventors...
this theorem in Problems Inform. Transmission, Gregory Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
also presents this theorem in J. ACM; Chaitin's paper was submitted October 1966, revised in December 1968 and cites both Solomonoff's and Kolmogorov's papers.
The theorem says that among algorithms that decode strings from their descriptions (codes) there exists an optimal one. This algorithm, for all strings, allows codes as short as allowed by any other algorithm up to an additive constant that depends on the algorithms, but not on the strings themselves. Solomonoff used this algorithm, and the code lengths it allows, to define a string's `universal probability' on which inductive inference of a string's subsequent digits can be based. Kolmogorov used this theorem to define several functions of strings: complexity, randomness, and information.
When Kolmogorov became aware of Solomonoff's work, he acknowledged Solomonoff's priority For several years, Solomonoff's work was better known in the Soviet Union than in the Western World. The general consensus in the scientific community, however, was to associate this type of complexity with Kolmogorov, who was concerned with randomness of a sequence while Algorithmic Probability became associated with Solomonoff, who focused on prediction using his invention of the universal a priori probability distribution.
There are several other variants of Kolmogorov complexity or algorithmic information. The most widely used one is based on self-delimiting programs and is mainly due to Leonid Levin
Leonid Levin
-External links:* at Boston University....
(1974).
An axiomatic approach to Kolmogorov complexity based on Blum axioms
Blum axioms
In computational complexity theory the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable functions. The axioms were first defined by Manuel Blum in 1967....
(Blum 1967) was introduced by Mark Burgin in the paper presented for publication by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
(Burgin 1982).
Some consider that naming the concept "Kolmogorov complexity" is an example of the Matthew effect
Matthew effect (sociology)
In sociology, the Matthew effect is the phenomenon where "the rich get richer and the poor get poorer". Those who possess power and economic or social capital can leverage those resources to gain more power or capital. The term was first coined by sociologist Robert K...
.
Basic results
In the following discussion let K(s) be the complexity of the string s.It is not hard to see that the minimal description of a string cannot be too much larger than the string itself: the program GenerateFixedString above that outputs s is a fixed amount larger than s.
Theorem. There is a constant c such that
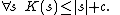
Incomputability of Kolmogorov complexity
The first result is that there is no way to effectively compute K.Theorem. K is not a computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
.
In other words, there is no program which takes a string s as input and produces the integer K(s) as output. We show this by contradiction by making a program that creates a string that should only be able to be created by a longer program. Suppose there is a program
function KolmogorovComplexity(string s)
that takes as input a string s and returns K(s). Now consider the program
function GenerateComplexString(int n)
for i = 1 to infinity:
for each string s of length exactly i
if KolmogorovComplexity(s) >= n
return s
quit
This program calls KolmogorovComplexity as a subroutine. This program tries every string, starting with the shortest, until it finds a string with complexity at least n, then returns that string. Therefore, given any positive integer n, it produces a string with Kolmogorov complexity at least as great as n. The program itself has a fixed length U. The input to the program GenerateComplexString is an integer n; here, the size of n is measured by the number of bits required to represent n which is log2(n). Now consider the following program:
function GenerateParadoxicalString
return GenerateComplexString(n0)
This program calls GenerateComplexString as a subroutine and also has a free parameter
n0. This program outputs a string s whose complexity is at least n0. By an auspicious choice of the parameter n0 we will arrive at a contradiction. To choose this value, note s is described by the program GenerateParadoxicalString whose length is at most
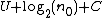
where C is the "overhead" added by the program GenerateParadoxicalString. Since n grows faster than log2(n), there exists a value n0 such that

But this contradicts the definition of s having a complexity at least n0. That is, by the definition of K(s), the string s returned by GenerateParadoxicalString is only supposed to be able to be generated by a program of length n0 or longer, but GenerateParadoxicalString is shorter than n0. Thus the program named "KolmogorovComplexity" cannot actually computably find the complexity of arbitrary strings.
This is proof by contradiction where the contradiction is similar to the Berry paradox
Berry paradox
The Berry paradox is a self-referential paradox arising from the expression "the smallest possible integer not definable by a given number of words". Bertrand Russell, the first to discuss the paradox in print, attributed it to G. G...
: "Let n be the smallest positive integer that cannot be defined in fewer than twenty English words." It is also possible to show the uncomputability of K by reduction from the uncomputability of the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
H, since K and H are Turing-equivalent
Turing degree
In computer science and mathematical logic the Turing degree or degree of unsolvability of a set of natural numbers measures the level of algorithmic unsolvability of the set...
.http://www.daimi.au.dk/~bromille/DC05/Kolmogorov.pdf
In the programming languages community there is a corollary known as the full employment theorem
Full employment theorem
In computer science and mathematics, the term full employment theorem has been used to refer to a theorem showing that no algorithm can optimally perform a particular task done by some class of professionals. The name arises because such a theorem ensures that there is endless scope to keep...
, stating there is no perfect size-optimizing compiler.
Chain rule for Kolmogorov complexity
The chain rule for Kolmogorov complexity states that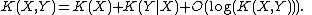
It states that the shortest program that reproduces X and Y is no more than a logarithmic term larger than a program to reproduce X and a program to reproduce Y given X. Using this statement one can define an analogue of mutual information for Kolmogorov complexity.
Compression
It is straightforward to compute upper bounds for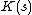 : simply compress
: simply compressData compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
the string
 with some method, implement the corresponding decompressor in the chosen language, concatenate the decompressor to the compressed string, and measure the resulting string's length.
with some method, implement the corresponding decompressor in the chosen language, concatenate the decompressor to the compressed string, and measure the resulting string's length.A string s is compressible by a number c if it has a description whose length does not exceed
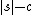 . This is equivalent to saying
. This is equivalent to saying  . Otherwise s is incompressible by c. A string incompressible by 1 is said to be simply incompressible; by the pigeonhole principle which applies because every compressed string maps to only one uncompressed string, incompressible string
. Otherwise s is incompressible by c. A string incompressible by 1 is said to be simply incompressible; by the pigeonhole principle which applies because every compressed string maps to only one uncompressed string, incompressible stringIncompressible string
An incompressible string is one that cannot be compressed because it lacks sufficient repeating sequences. Whether a string is compressible will often depend on the algorithm being used...
s must exist, since there are
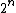 bit strings of length n but only 2n − 1 shorter strings, that is strings of length less than n, i.e. with length 0,1,...,n-1.
bit strings of length n but only 2n − 1 shorter strings, that is strings of length less than n, i.e. with length 0,1,...,n-1.For the same reason, most strings are complex in the sense that they cannot be significantly compressed:
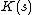 is not much smaller than
is not much smaller than 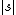 , the length of s in bits. To make this precise, fix a value of n. There are
, the length of s in bits. To make this precise, fix a value of n. There are 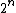 bitstrings of length n. The uniform probability
bitstrings of length n. The uniform probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
distribution on the space of these bitstrings assigns exactly equal weight
 to each string of length n.
to each string of length n.Theorem. With the uniform probability distribution on the space of bitstrings of length n, the probability that a string is incompressible by c is at least
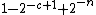 .
.To prove the theorem, note that the number of descriptions of length not exceeding
 is given by the geometric series:
is given by the geometric series: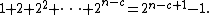
There remain at least
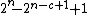
many bitstrings of length n that are incompressible by c. To determine the probability divide by
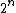 .
.Chaitin's incompleteness theorem
We know that, in the set of all possible strings, most strings are complex in the sense that they cannot be described in any significantly "compressed" way. However, it turns out that the fact that a specific string is complex cannot be formally proved, if the string's complexity is above a certain threshold. The precise formalization is as follows. First fix a particular axiomatic systemAxiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
S for the natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s. The axiomatic system has to be powerful enough so that to certain assertions A about complexity of strings one can associate a formula FA in S. This association must have the following property: if FA is provable from the axioms of S, then the corresponding assertion A is true. This "formalization" can be achieved either by an artificial encoding such as a Gödel numbering or by a formalization which more clearly respects the intended interpretation of S.
Theorem. There exists a constant L (which only depends on the particular axiomatic system and the choice of description language) such that there does not exist a string s for which the statement
(as formalized in S) can be proven within the axiomatic system S.
Note that by the abundance of nearly incompressible strings, the vast majority of those statements must be true.
The proof of this result is modeled on a self-referential construction used in Berry's paradox. The proof is by contradiction. If the theorem were false, then
- Assumption (X): For any integer n there exists a string s for which there is a proof in S of the formula "K(s) ≥ n" (which we assume can be formalized in S).
We can find an effective enumeration of all the formal proofs in S by some procedure
function NthProof(int n)
which takes as input n and outputs some proof. This function
enumerates all proofs. Some of these are proofs for formulas we do not
care about here (examples of proofs which will be listed by the procedure NthProof are the various known proofs of the law of quadratic reciprocity, those of Fermat's little theorem
Fermat's little theorem
Fermat's little theorem states that if p is a prime number, then for any integer a, a p − a will be evenly divisible by p...
or the proof of Fermat's last theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
all translated into the formal language of S). Some of these are complexity formulas of the form K(s) ≥ n where s and n are constants in the language of S. There is a program
function NthProofProvesComplexityFormula(int n)
which determines whether the nth proof actually proves
a complexity formula K(s) ≥ L. The strings s and
the integer L in turn are computable by programs:
function StringNthProof(int n)
function ComplexityLowerBoundNthProof(int n)
Consider the following program
function GenerateProvablyComplexString(int n)
for i = 1 to infinity:
if NthProofProvesComplexityFormula(i) and ComplexityLowerBoundNthProof(i) ≥ n
return StringNthProof(i)
quit
Given an n, this program tries every proof until it finds a string
and a proof in the formal system
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
S of the formula K(s) ≥ L for some L ≥ n. The program
terminates by our Assumption (X). Now this program has a length U.
There is an integer n0 such that U + log2(n0) + C < n0, where C is the overhead cost of
function GenerateProvablyParadoxicalString
return GenerateProvablyComplexString(n0)
quit
The program GenerateProvablyParadoxicalString outputs a string s for which there exists an L such that K(s) ≥ L can be formally proved in S with L ≥ n0. In particular K(s) ≥
n0 is true. However, s is also described by a program of length
U + log2(n0) + C so its complexity is less than n0. This contradiction proves Assumption (X) cannot hold.
Similar ideas are used to prove the properties of Chaitin's constant
Chaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
.
Minimum message length
The minimum message lengthMinimum message length
Minimum message length is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct...
principle of statistical and inductive inference and machine learning was developed by C.S. Wallace
Chris Wallace (computer scientist)
Professor Christopher Stewart Wallace was an Australian computer scientist notable for having devised:...
and D.M. Boulton in 1968. MML is Bayesian
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
(it incorporates prior beliefs) and
information-theoretic. It has the desirable properties of statistical
invariance (the inference transforms with a re-parametrisation, such as from
polar coordinates to Cartesian coordinates), statistical consistency (even
for very hard problems, MML will converge to any underlying model) and efficiency (the MML model will converge to any true underlying model about as quickly as is possible). C.S. Wallace and D.L. Dowe (1999) showed a formal connection between MML and algorithmic information theory (or Kolmogorov complexity).
Kolmogorov randomness
Kolmogorov randomness (also called algorithmic randomness) defines a string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
(usually of bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s) as being random
Randomness
Randomness has somewhat differing meanings as used in various fields. It also has common meanings which are connected to the notion of predictability of events....
if and only if it is shorter than any computer program
Computer program
A computer program is a sequence of instructions written to perform a specified task with a computer. A computer requires programs to function, typically executing the program's instructions in a central processor. The program has an executable form that the computer can use directly to execute...
that can produce that string. This definition of randomness is critically dependent on the definition of Kolmogorov complexity. To make this definition complete, a computer has to be specified, usually a Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
. According to the above definition of randomness, a random string is also an "incompressible" string, in the sense that it is impossible to give a representation of the string using a program whose length is shorter than the length of the string itself. However, according to this definition, most strings shorter than a certain length end up being (Chaitin-Kolmogorovically) random because the best one can do with very small strings is to write a program that simply prints these strings.
See also
- Data compressionData compressionIn computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
- Inductive inferenceInductive inferenceAround 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
- Kolmogorov structure functionKolmogorov structure functionIn 1974 Kolmogorov proposed a non-probabilistic approach to statistics and model selection. Let each data be a finite binary string and models be finite sets of binary strings...
- Important publications in algorithmic information theory
- Levenshtein distanceLevenshtein distanceIn information theory and computer science, the Levenshtein distance is a string metric for measuring the amount of difference between two sequences...
- Grammar inductionGrammar InductionGrammatical induction, also known as grammatical inference or syntactic pattern recognition, refers to the process in machine learning of learning a formal grammar from a set of observations, thus constructing a model which accounts for the characteristics of the observed objects...
External links
- The Legacy of Andrei Nikolaevich Kolmogorov
- Chaitin's online publications
- Solomonoff's IDSIA page
- Generalizations of algorithmic information by J. Schmidhuber
- Ming Li and Paul Vitanyi, An Introduction to Kolmogorov Complexity and Its Applications, 2nd Edition, Springer Verlag, 1997.
- Tromp's lambda calculus computer model offers a concrete definition of K
- Universal AI based on Kolmogorov Complexity ISBN 3-540-22139-5 by M. HutterMarcus HutterMarcus Hutter is a German computer scientist and professor at the Australian National University. Hutter was born and educated in Munich, where he studied physics and computer science...
: ISBN 3-540-22139-5 - David Dowe's Minimum Message Length (MML) and Occam's razor pages.
- P. Grunwald, M. A. Pitt and I. J. Myung (ed.), Advances in Minimum Description Length: Theory and Applications, M.I.T. Press, April 2005, ISBN 0-262-07262-9.