
Algorithmic information theory
Encyclopedia
Algorithmic information theory is a subfield of information theory
and computer science
that concerns itself with the relationship between computation
and information. According to Gregory Chaitin
, it is "the result of putting Shannon's information theory and Turing
's computability theory into a cocktail shaker and shaking vigorously."
s (or other data structure
s). Because most mathematical objects can be described in terms of strings, or as the limit
of a sequence
of strings, it can be used to study a wide variety of mathematical objects, including integer
s and real number
s.
This use of the term "information" might be a bit misleading, as it depends upon the concept of compressibility. Informally, from the point of view of algorithmic information theory, the information content of a string is equivalent to the length of the shortest possible self-contained representation of that string. A self-contained representation is essentially a program – in some fixed but otherwise irrelevant universal programming language
– that, when run, outputs the original string.
From this point of view, a 3000 page encyclopedia actually contains less information than 3000 pages of completely random letters, despite the fact that the encyclopedia is much more useful. This is because to reconstruct the entire sequence of random letters, one must know, more or less, what every single letter is. On the other hand, if every vowel were removed from the encyclopedia, someone with reasonable knowledge of the English language could reconstruct it, just as one could likely reconstruct the sentence "Ths sntnc hs lw nfrmtn cntnt" from the context and consonants present. For this reason, high-information strings and sequences are sometimes called "random"; people also sometimes attempt to distinguish between "information" and "useful information" and attempt to provide rigorous definitions for the latter, with the idea that the random letters may have more information than the encyclopedia, but the encyclopedia has more "useful" information.
Unlike classical information theory, algorithmic information theory gives formal
, rigorous definitions of a random string
and a random infinite sequence
that do not depend on physical or philosophical intuition
s about nondeterminism
or likelihood
. (The set of random strings depends on the choice of the universal Turing machine
used to define Kolmogorov complexity, but any choice
gives identical asymptotic results because the Kolmogorov complexity of a string is invariant up to an additive constant depending only on the choice of universal Turing machine. For this reason the set of random infinite sequences is independent of the choice of universal machine.)
Some of the results of algorithmic information theory, such as Chaitin's incompleteness theorem, appear to challenge common mathematical and philosophical intuitions. Most notable among these is the construction of Chaitin's constant
Ω, a real number which expresses the probability that a self-delimiting universal Turing machine will halt
when its input is supplied by flips of a fair coin (sometimes thought of as the probability that a random computer program will eventually halt). Although Ω is easily defined, in any consistent axiom
atizable theory
one can only compute finitely many digits of Ω, so it is in some sense unknowable, providing an absolute limit on knowledge that is reminiscent of Gödel's Incompleteness Theorem. Although the digits of Ω cannot be determined, many properties of Ω are known; for example, it is an algorithmically random sequence
and thus its binary digits are evenly distributed (in fact it is normal
).
, who published the basic ideas on which the field is based as part of his invention of algorithmic probability
- a way to overcome serious problems associated with the application of Bayes rules in statistics. He first described his results at a Conference at Caltech in 1960, and in a report, Feb. 1960, "A Preliminary Report on a General Theory of Inductive Inference." Algorithmic information theory was later developed independently by Andrey Kolmogorov
, in 1965 and Gregory Chaitin
, around 1966.
There are several variants of Kolmogorov complexity or algorithmic information; the most widely used one is based on self-delimiting programs and is mainly due to Leonid Levin
(1974). Per Martin-Löf
also contributed significantly to the information theory of infinite sequences. An axiomatic approach to algorithmic information theory based on Blum axioms
(Blum 1967) was introduced by Mark Burgin in a paper presented for publication by Andrey Kolmogorov
(Burgin 1982). The axiomatic approach encompasses other approaches in the algorithmic information theory. It is possible to treat different measures of algorithmic information as particular cases of axiomatically defined measures of algorithmic information. Instead of proving similar theorems, such as the basic invariance theorem, for each particular measure, it is possible to easily deduce all such results from one corresponding theorem proved in the axiomatic setting. This is a general advantage of the axiomatic approach in mathematics. The axiomatic approach to algorithmic information theory was further developed in the book (Burgin 2005) and applied to software metrics (Burgin and Debnath, 2003; Debnath and Burgin, 2003).
of the string is at least the length of the string. A simple counting argument shows that some strings of any given length are random, and almost all strings are very close to being random. Since Kolmogorov complexity depends on a fixed choice of universal Turing machine (informally, a fixed "description language" in which the "descriptions" are given), the collection of random strings does depend on the choice of fixed universal machine. Nevertheless, the collection of random strings, as a whole, has similar properties regardless of the fixed machine, so one can (and often does) talk about the properties of random strings as a group without having to first specify a universal machine.
An infinite binary sequence is said to be random if, for some constant c, for all n, the Kolmogorov complexity
of the initial segment of length n of the sequence is at least n − c. Importantly, the complexity used here is prefix-free complexity; if plain complexity were used, there would be no random sequences. However, with this definition, it can be shown that almost every sequence (from the point of view of the standard measure
- "fair coin" or Lebesgue measure
– on the space of infinite binary sequences) is random. Also, since it can be shown that the Kolmogorov complexity relative to two different universal machines differs by at most a constant, the collection of random infinite sequences does not depend on the choice of universal machine (in contrast to finite strings). This definition of randomness is usually called Martin-Löf randomness, after Per Martin-Löf
, to distinguish it from other similar notions of randomness. It is also sometimes called 1-randomness to distinguish it from other stronger notions of randomness (2-randomness, 3-randomness, etc.).
(Related definitions can be made for alphabets other than the set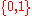 .)
.)
The information content or complexity of an object can be measured by the length of its shortest description. For instance the string
has the short description "32 repetitions of '01'", while
presumably has no simple description other than writing down the string itself.
More formally, the Algorithmic Complexity (AC) of a string x is defined as the length of the shortest program that computes or outputs x, where the program is run on some fixed reference universal computer.
A closely related notion is the probability that a universal computer outputs some string x when fed with a program chosen at random. This Algorithmic "Solomon-off" Probability (AP) is key in addressing the old philosophical problem of induction in a formal way.
The major drawback of AC and AP are their incomputability. Time-bounded "Levin" complexity penalizes a slow program by adding the logarithm of its running time to its length. This leads to computable variants of AC and AP, and Universal "Levin" Search (US) solves all inversion problems in optimal (apart from some unrealistically large multiplicative constant) time.
AC and AP also allow a formal and rigorous definition of randomness of individual strings do not depend on physical or philosophical intuitions about non-determinism or likelihood. Roughly, a string is Algorithmic "Martin-Loef" Random (AR) if it is incompressible in the sense that its algorithmic complexity is equal to its length.
AC, AP, and AR are the core sub-disciplines of AIT, but AIT spawns into many other areas. It serves as the foundation of the Minimum Description Length (MDL) principle, can simplify proofs in computational complexity theory, has been used to define a universal similarity metric between objects, solves the Maxwell daemon problem, and many others.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
that concerns itself with the relationship between computation
Theory of computation
In theoretical computer science, the theory of computation is the branch that deals with whether and how efficiently problems can be solved on a model of computation, using an algorithm...
and information. According to Gregory Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
, it is "the result of putting Shannon's information theory and Turing
Alan Turing
Alan Mathison Turing, OBE, FRS , was an English mathematician, logician, cryptanalyst, and computer scientist. He was highly influential in the development of computer science, providing a formalisation of the concepts of "algorithm" and "computation" with the Turing machine, which played a...
's computability theory into a cocktail shaker and shaking vigorously."
Overview
Algorithmic information theory principally studies complexity measures on stringString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
s (or other data structure
Data structure
In computer science, a data structure is a particular way of storing and organizing data in a computer so that it can be used efficiently.Different kinds of data structures are suited to different kinds of applications, and some are highly specialized to specific tasks...
s). Because most mathematical objects can be described in terms of strings, or as the limit
Limit of a sequence
The limit of a sequence is, intuitively, the unique number or point L such that the terms of the sequence become arbitrarily close to L for "large" values of n...
of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of strings, it can be used to study a wide variety of mathematical objects, including integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s.
This use of the term "information" might be a bit misleading, as it depends upon the concept of compressibility. Informally, from the point of view of algorithmic information theory, the information content of a string is equivalent to the length of the shortest possible self-contained representation of that string. A self-contained representation is essentially a program – in some fixed but otherwise irrelevant universal programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
– that, when run, outputs the original string.
From this point of view, a 3000 page encyclopedia actually contains less information than 3000 pages of completely random letters, despite the fact that the encyclopedia is much more useful. This is because to reconstruct the entire sequence of random letters, one must know, more or less, what every single letter is. On the other hand, if every vowel were removed from the encyclopedia, someone with reasonable knowledge of the English language could reconstruct it, just as one could likely reconstruct the sentence "Ths sntnc hs lw nfrmtn cntnt" from the context and consonants present. For this reason, high-information strings and sequences are sometimes called "random"; people also sometimes attempt to distinguish between "information" and "useful information" and attempt to provide rigorous definitions for the latter, with the idea that the random letters may have more information than the encyclopedia, but the encyclopedia has more "useful" information.
Unlike classical information theory, algorithmic information theory gives formal
Formal system
In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...
, rigorous definitions of a random string
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
and a random infinite sequence
Algorithmically random sequence
Intuitively, an algorithmically random sequence is an infinite sequence ofbinary digits that appears random to any algorithm...
that do not depend on physical or philosophical intuition
Intuition (knowledge)
Intuition is the ability to acquire knowledge without inference or the use of reason. "The word 'intuition' comes from the Latin word 'intueri', which is often roughly translated as meaning 'to look inside'’ or 'to contemplate'." Intuition provides us with beliefs that we cannot necessarily justify...
s about nondeterminism
Nondeterminism
Nondeterminism may refer to:* Nondeterministic programming * Nondeterministic algorithm * Non-deterministic Turing machine * Indeterminacy in computation * Indeterminism...
or likelihood
Likelihood
Likelihood is a measure of how likely an event is, and can be expressed in terms of, for example, probability or odds in favor.-Likelihood function:...
. (The set of random strings depends on the choice of the universal Turing machine
Universal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
used to define Kolmogorov complexity, but any choice
gives identical asymptotic results because the Kolmogorov complexity of a string is invariant up to an additive constant depending only on the choice of universal Turing machine. For this reason the set of random infinite sequences is independent of the choice of universal machine.)
Some of the results of algorithmic information theory, such as Chaitin's incompleteness theorem, appear to challenge common mathematical and philosophical intuitions. Most notable among these is the construction of Chaitin's constant
Chaitin's constant
In the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
Ω, a real number which expresses the probability that a self-delimiting universal Turing machine will halt
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
when its input is supplied by flips of a fair coin (sometimes thought of as the probability that a random computer program will eventually halt). Although Ω is easily defined, in any consistent axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
atizable theory
Theory (mathematical logic)
In mathematical logic, a theory is a set of sentences in a formal language. Usually a deductive system is understood from context. An element \phi\in T of a theory T is then called an axiom of the theory, and any sentence that follows from the axioms is called a theorem of the theory. Every axiom...
one can only compute finitely many digits of Ω, so it is in some sense unknowable, providing an absolute limit on knowledge that is reminiscent of Gödel's Incompleteness Theorem. Although the digits of Ω cannot be determined, many properties of Ω are known; for example, it is an algorithmically random sequence
Algorithmically random sequence
Intuitively, an algorithmically random sequence is an infinite sequence ofbinary digits that appears random to any algorithm...
and thus its binary digits are evenly distributed (in fact it is normal
Normal number
In mathematics, a normal number is a real number whose infinite sequence of digits in every base b is distributed uniformly in the sense that each of the b digit values has the same natural density 1/b, also all possible b2 pairs of digits are equally likely with density b−2,...
).
History
Algorithmic information theory was founded by Ray SolomonoffRay Solomonoff
Ray Solomonoff was the inventor of algorithmic probability, and founder of algorithmic information theory, He was an originator of the branch of artificial intelligence based on machine learning, prediction and probability...
, who published the basic ideas on which the field is based as part of his invention of algorithmic probability
Algorithmic probability
In algorithmic information theory, algorithmic probability is a method of assigning a probability to each hypothesis that explains a given observation, with the simplest hypothesis having the highest probability and the increasingly complex hypotheses receiving increasingly small probabilities...
- a way to overcome serious problems associated with the application of Bayes rules in statistics. He first described his results at a Conference at Caltech in 1960, and in a report, Feb. 1960, "A Preliminary Report on a General Theory of Inductive Inference." Algorithmic information theory was later developed independently by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
, in 1965 and Gregory Chaitin
Gregory Chaitin
Gregory John Chaitin is an Argentine-American mathematician and computer scientist.-Mathematics and computer science:Beginning in 2009 Chaitin has worked on metabiology, a field parallel to biology dealing with the random evolution of artificial software instead of natural software .Beginning in...
, around 1966.
There are several variants of Kolmogorov complexity or algorithmic information; the most widely used one is based on self-delimiting programs and is mainly due to Leonid Levin
Leonid Levin
-External links:* at Boston University....
(1974). Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
also contributed significantly to the information theory of infinite sequences. An axiomatic approach to algorithmic information theory based on Blum axioms
Blum axioms
In computational complexity theory the Blum axioms or Blum complexity axioms are axioms which specify desirable properties of complexity measures on the set of computable functions. The axioms were first defined by Manuel Blum in 1967....
(Blum 1967) was introduced by Mark Burgin in a paper presented for publication by Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
(Burgin 1982). The axiomatic approach encompasses other approaches in the algorithmic information theory. It is possible to treat different measures of algorithmic information as particular cases of axiomatically defined measures of algorithmic information. Instead of proving similar theorems, such as the basic invariance theorem, for each particular measure, it is possible to easily deduce all such results from one corresponding theorem proved in the axiomatic setting. This is a general advantage of the axiomatic approach in mathematics. The axiomatic approach to algorithmic information theory was further developed in the book (Burgin 2005) and applied to software metrics (Burgin and Debnath, 2003; Debnath and Burgin, 2003).
Precise definitions
A binary string is said to be random if the Kolmogorov complexityKolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of the string is at least the length of the string. A simple counting argument shows that some strings of any given length are random, and almost all strings are very close to being random. Since Kolmogorov complexity depends on a fixed choice of universal Turing machine (informally, a fixed "description language" in which the "descriptions" are given), the collection of random strings does depend on the choice of fixed universal machine. Nevertheless, the collection of random strings, as a whole, has similar properties regardless of the fixed machine, so one can (and often does) talk about the properties of random strings as a group without having to first specify a universal machine.
An infinite binary sequence is said to be random if, for some constant c, for all n, the Kolmogorov complexity
Kolmogorov complexity
In algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
of the initial segment of length n of the sequence is at least n − c. Importantly, the complexity used here is prefix-free complexity; if plain complexity were used, there would be no random sequences. However, with this definition, it can be shown that almost every sequence (from the point of view of the standard measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
- "fair coin" or Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
– on the space of infinite binary sequences) is random. Also, since it can be shown that the Kolmogorov complexity relative to two different universal machines differs by at most a constant, the collection of random infinite sequences does not depend on the choice of universal machine (in contrast to finite strings). This definition of randomness is usually called Martin-Löf randomness, after Per Martin-Löf
Per Martin-Löf
Per Erik Rutger Martin-Löf is a Swedish logician, philosopher, and mathematical statistician. He is internationally renowned for his work on the foundations of probability, statistics, mathematical logic, and computer science. Since the late 1970s, Martin-Löf's publications have been mainly in...
, to distinguish it from other similar notions of randomness. It is also sometimes called 1-randomness to distinguish it from other stronger notions of randomness (2-randomness, 3-randomness, etc.).
(Related definitions can be made for alphabets other than the set
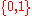 .)
.)Specific sequence
Algorithmic information theory (AIT) is the information theory of individual objects, using computer science, and concerns itself with the relationship between computation, information, and randomness.The information content or complexity of an object can be measured by the length of its shortest description. For instance the string
"0101010101010101010101010101010101010101010101010101010101010101"has the short description "32 repetitions of '01'", while
"1100100001100001110111101110110011111010010000100101011110010110"presumably has no simple description other than writing down the string itself.
More formally, the Algorithmic Complexity (AC) of a string x is defined as the length of the shortest program that computes or outputs x, where the program is run on some fixed reference universal computer.
A closely related notion is the probability that a universal computer outputs some string x when fed with a program chosen at random. This Algorithmic "Solomon-off" Probability (AP) is key in addressing the old philosophical problem of induction in a formal way.
The major drawback of AC and AP are their incomputability. Time-bounded "Levin" complexity penalizes a slow program by adding the logarithm of its running time to its length. This leads to computable variants of AC and AP, and Universal "Levin" Search (US) solves all inversion problems in optimal (apart from some unrealistically large multiplicative constant) time.
AC and AP also allow a formal and rigorous definition of randomness of individual strings do not depend on physical or philosophical intuitions about non-determinism or likelihood. Roughly, a string is Algorithmic "Martin-Loef" Random (AR) if it is incompressible in the sense that its algorithmic complexity is equal to its length.
AC, AP, and AR are the core sub-disciplines of AIT, but AIT spawns into many other areas. It serves as the foundation of the Minimum Description Length (MDL) principle, can simplify proofs in computational complexity theory, has been used to define a universal similarity metric between objects, solves the Maxwell daemon problem, and many others.
See also
- Kolmogorov complexityKolmogorov complexityIn algorithmic information theory , the Kolmogorov complexity of an object, such as a piece of text, is a measure of the computational resources needed to specify the object...
- Algorithmically random sequenceAlgorithmically random sequenceIntuitively, an algorithmically random sequence is an infinite sequence ofbinary digits that appears random to any algorithm...
- Algorithmic probabilityAlgorithmic probabilityIn algorithmic information theory, algorithmic probability is a method of assigning a probability to each hypothesis that explains a given observation, with the simplest hypothesis having the highest probability and the increasingly complex hypotheses receiving increasingly small probabilities...
- Chaitin's constantChaitin's constantIn the computer science subfield of algorithmic information theory, a Chaitin constant or halting probability is a real number that informally represents the probability that a randomly constructed program will halt...
- Chaitin–Kolmogorov randomness
- Computationally indistinguishable
- Distribution ensemble
- Epistemology
- Invariance theoremInvariance theoremIn algorithmic information theory, the invariance theorem, originally proved by Ray Solomonoff, states that a universal Turing machine provides an optimal means of description, up to an additive constant...
- Limits to knowledge
- Minimum description lengthMinimum description lengthThe minimum description length principle is a formalization of Occam's Razor in which the best hypothesis for a given set of data is the one that leads to the best compression of the data. MDL was introduced by Jorma Rissanen in 1978...
- Minimum message lengthMinimum message lengthMinimum message length is a formal information theory restatement of Occam's Razor: even when models are not equal in goodness of fit accuracy to the observed data, the one generating the shortest overall message is more likely to be correct...
- Pseudorandom ensemble
- Pseudorandom generatorPseudorandom generatorIn theoretical computer science, a pseudorandom generator is a deterministic procedure that produces a pseudorandom distribution from a short uniform input, known as a random seed.-Definition:...
- Simplicity theorySimplicity theorySimplicity theory is a cognitive theory that seeks to explain the attractiveness of situations or events to human minds. It isbased on work done by scientists like Nick Chater, Paul Vitanyi, Jean-Louis Dessalles, Jürgen Schmidhuber...
- Uniform ensemble
External links
Further reading
- Blum, M. (1967) On the Size of Machines, Information and Control, v. 11, pp. 257–265
- Blum M. (1967a) A Machine-independent Theory of Complexity of Recursive Functions, Journal of the ACM, v. 14, No.2, pp. 322–336
- Burgin, M. (1982) Generalized Kolmogorov complexity and duality in theory of computations, Soviet Math. Dokl., v.25, No. 3, pp. 19–23
- Burgin, M. (1990) Generalized Kolmogorov Complexity and other Dual Complexity Measures, Cybernetics, No. 4, pp. 21–29
- Burgin, M. Super-recursive algorithms, Monographs in computer science, Springer, 2005
- Calude, C.S. (1996) Algorithmic information theory: Open problems, J. UCS, v. 2, pp. 439–441
- Calude, C.S. Information and Randomness: An Algorithmic Perspective, (Texts in Theoretical Computer Science. An EATCS Series), Springer-Verlag, Berlin, 2002
- Chaitin, G.J. (1966) On the Length of Programs for Computing Finite Binary Sequences, J. Association for Computing Machinery, v. 13, No. 4, pp. 547–569
- Chaitin, G.J. (1969) On the Simplicity and Speed of Programs for Computing Definite Sets of Natural Numbers, J. Association for Computing Machinery, v. 16, pp. 407–412
- Chaitin, G.J. (1975) A Theory of Program Size Formally Identical to Information Theory, J. Association for Computing Machinery, v. 22, No. 3, pp. 329–340
- Chaitin, G.J. (1977) Algorithmic information theory, IBM Journal of Research and Development, v.21, No. 4, 350-359
- Chaitin, G.J. Algorithmic Information Theory, Cambridge University Press, Cambridge, 1987
- Kolmogorov, A.N. (1965) Three approaches to the definition of the quantity of information, Problems of Information Transmission, No. 1, pp. 3–11
- Kolmogorov, A.N. (1968) Logical basis for information theory and probability theory, IEEE Trans. Inform. Theory, vol. IT-14, pp. 662–664
- Levin, L. A. (1974) Laws of information (nongrowth) and aspects of the foundation of probability theory, Problems of Information Transmission, v. 10, No. 3, pp. 206–210
- Levin, L.A. (1976) Various Measures of Complexity for Finite Objects (Axiomatic Description), Soviet Math. Dokl., v. 17, pp. 522–526
- Li, M., and Vitanyi, P. An Introduction to Kolmogorov Complexity and its Applications, Springer-Verlag, New York, 1997
- Solomonoff, R.J. (1960) A Preliminary Report on a General Theory of Inductive Inference, Technical Report ZTB-138, Zator Company, Cambridge, Mass.
- Solomonoff, R.J. (1964) A Formal Theory of Inductive Inference, Information and Control, v. 7, No. 1, pp. 1–22; No.2, pp. 224–254
- Solomonoff, R.J. (2009) Algorithmic Probability: Theory and Applications, Information Theory and Statistical Learning, Springer NY, Emmert-Streib, F. and Dehmer, M. (Eds), ISBN 978-0-387-84815-0.
- Van Lambagen, (1989) Algorithmic Information Theory, Journal for Symbolic Logic, v. 54, pp. 1389–1400
- Zurek, W.H. (1991) Algorithmic Information Content, Church-Turing Thesis, physical entropy, and Maxwell’s demon, in Complexity, Entropy and the Physics of Information, (Zurek, W.H., Ed.) Addison-Wesley, pp. 73–89
- Zvonkin, A.K. and Levin, L. A. (1970) The Complexity of Finite Objects and the Development of the Concepts of Information and Randomness by Means of the Theory of Algorithms, Russian Mathematics Surveys, v. 256, pp. 83–124

