
Spray (mathematics)
Encyclopedia
In differential geometry, a spray is a vector field
H on the tangent bundle
TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→ΦHt(ξ)∈TM obey the rule ΦHt(λξ)=ΦHλt(ξ) in positive reparameterizations. If this requirement is dropped, H is called a semispray.
Sprays arise naturally in Riemannian
and Finsler geometry as the geodesic sprays, whose integral curve
s are precisely the tangent curves of locally length minimizing curves.
Semisprays arise naturally as the extremal curves of action integrals in Lagrangian mechanics
. Generalizing all these examples, any (possibly nonlinear) connection on M induces a semispray H, and conversely, any semispray H induces a torsion-free nonlinear connection on M. If the original connection is torsion-free it coincides with the connection induced by H, and homogeneous torsion-free connections are in one-to-one correspondence with full sprays.
and (TM,πTM,M) its tangent bundle. Then a vector field H on TM (that is, a section
of the double tangent bundle
TTM) is a semispray on M, if any of the three following equivalent conditions holds:
A semispray H on M is a (full) spray if any of the following equivalent conditions hold:
Let (xi,ξi) be the local coordinates on TM associated with the local coordinates (xi) on M using the coordinate basis on each tangent space. Then H is a semispray on M if and only if it has a local representation of the form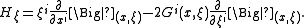
on each associated coordinate system on TM. The semispray H is a (full) spray, if and only if the spray coefficients Gi satisfy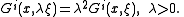
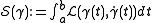 .
.
In the associated coordinates on TM the first variation of the action integral reads as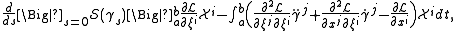
where X:[a,b]→R is the variation vector field associated with the variation γs:[a,b]→M around γ(t) = γ0(t). This first variation formula can be recast in a more informative form by introducing the following concepts:
If the Legendre condition is satisfied, then dα∈Ω2(TM) is a symplectic form, and there exists a unique Hamiltonian vector field
H on TM corresponding to the Hamiltonian function E such that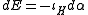 .
.
Let (Xi,Yi) be the components of the Hamiltonian vector field H in the associated coordinates on TM. Then
and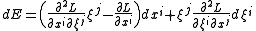
so we see that the Hamiltonian vector field H is a semispray on the configuration space M with the spray coefficients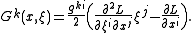
Now the first variational formula can be rewritten as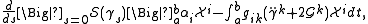
and we see γ[a,b]→M is stationary for the action integral with fixed end points if and only if its tangent curve γ':[a,b]→TM is an integral curve for the Hamiltonian vector field H. Hence the dynamics of mechanical systems are described by semisprays arising from action integrals.
and Finsler manifold
s are called geodesics. Using the framework of Lagrangian mechanics one can describe these curves with spray structures. Define a Lagrangian function on TM by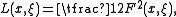
where F:TM→R is the Finsler function
. In the Riemannian case one uses F2(x,ξ) = gij(x)ξiξj. Now introduce the concepts from the section above. In the Riemannian case it turns out that the fundamental tensor gij(x,ξ) is simply the Riemannian metric gij(x). In the general case the homogeneity condition
of the Finsler-function implies the following formulae: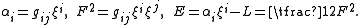
In terms of classical mechanical the last equation states that all the energy in the system (M,L) is in the kinetic form. Furthermore, one obtains the homogeneity properties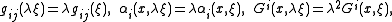
of which the last one says that the Hamiltonian vector field H for this mechanical system is a full spray. The constant speed geodesics of the underlying Finsler (or Riemannian) manifold are described by this spray for the following reasons:
Therefore a curve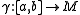 is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.
is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.
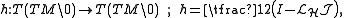
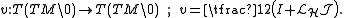
This connection on TM\0 always has a vanishing torsion tensor, which is defined as the Frölicher-Nijenhuis bracket
T=[J,v]. In more elementary terms the torsion can be defined as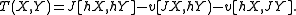
Introducing the canonical vector field V on TM\0 and the adjoint structure Θ of the induced connection the horizontal part of the semispray can be written as hH=ΘV. The vertical part ε=vH of the semispray is known as the first spray invariant, and the semispray H itself decomposes into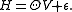
The first spray invariant is related to the tension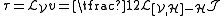
of the induced non-linear connection through the ordinary differential equation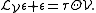
Therefore the first spray invariant ε (and hence the whole semi-spray H) can be recovered from the non-linear connection by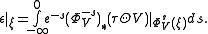
From this relation one also sees that the induced connection is homogeneous if and only if H is a full spray.
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
H on the tangent bundle
Tangent bundle
In differential geometry, the tangent bundle of a differentiable manifold M is the disjoint unionThe disjoint union assures that for any two points x1 and x2 of manifold M the tangent spaces T1 and T2 have no common vector...
TM that encodes a quasilinear second order system of ordinary differential equations on the base manifold M. Usually a spray is required to be homogeneous in the sense that its integral curves t→ΦHt(ξ)∈TM obey the rule ΦHt(λξ)=ΦHλt(ξ) in positive reparameterizations. If this requirement is dropped, H is called a semispray.
Sprays arise naturally in Riemannian
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
and Finsler geometry as the geodesic sprays, whose integral curve
Integral curve
In mathematics, an integral curve is a parametric curve that represents a specific solution to an ordinary differential equation or system of equations...
s are precisely the tangent curves of locally length minimizing curves.
Semisprays arise naturally as the extremal curves of action integrals in Lagrangian mechanics
Lagrangian mechanics
Lagrangian mechanics is a re-formulation of classical mechanics that combines conservation of momentum with conservation of energy. It was introduced by the Italian-French mathematician Joseph-Louis Lagrange in 1788....
. Generalizing all these examples, any (possibly nonlinear) connection on M induces a semispray H, and conversely, any semispray H induces a torsion-free nonlinear connection on M. If the original connection is torsion-free it coincides with the connection induced by H, and homogeneous torsion-free connections are in one-to-one correspondence with full sprays.
Formal definitions
Let M be a differentiable manifoldDifferentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
and (TM,πTM,M) its tangent bundle. Then a vector field H on TM (that is, a section
Section (fiber bundle)
In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
of the double tangent bundle
Double tangent bundle
In mathematics, particularly differential topology, the double tangent bundle or the second tangent bundle refers to the tangent bundle of the total space TM of the tangent bundle of a smooth manifold M...
TTM) is a semispray on M, if any of the three following equivalent conditions holds:
- (πTM)*Hξ = ξ.
- JH=V, where J is the tangent structure on TM and V is the canonical vector field on TM\0.
- j∘H=H, where j:TTM→TTM is the canonical flip and H is seen as a mapping TM→TTM.
A semispray H on M is a (full) spray if any of the following equivalent conditions hold:
- Hλξ = λ*(λHξ), where λ*:TTM→TTM is the push-forward of the multiplication λ:TM→TM by positive scalar λ>0.
- The Lie-derivative of H along the canonical vector field V satisfies [V,H]=H.
- The integral curves t→ΦHt(ξ)∈TM\0 of H satisfy ΦHt(λξ)=ΦHλt(ξ) for any λ>0.
Let (xi,ξi) be the local coordinates on TM associated with the local coordinates (xi) on M using the coordinate basis on each tangent space. Then H is a semispray on M if and only if it has a local representation of the form
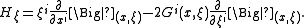
on each associated coordinate system on TM. The semispray H is a (full) spray, if and only if the spray coefficients Gi satisfy
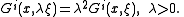
Semisprays in Lagrangian mechanics
A physical system is modeled in Lagrangian mechanics by a Lagrangian function L:TM→R on the tangent bundle of some configuration space M. The dynamical law is obtained from the Hamiltonian principle, which states that the time evolution γ:[a,b]→M of the state of the system is stationary for the action integral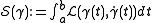 .
.In the associated coordinates on TM the first variation of the action integral reads as
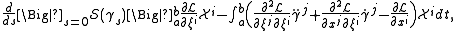
where X:[a,b]→R is the variation vector field associated with the variation γs:[a,b]→M around γ(t) = γ0(t). This first variation formula can be recast in a more informative form by introducing the following concepts:
- The covector
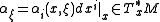 with
with  is the conjugate momentum of
is the conjugate momentum of  .
. - The corresponding one-form
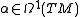 with
with 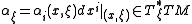 is the Hilbert-form associated with the Lagrangian.
is the Hilbert-form associated with the Lagrangian. - The bilinear form
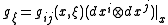 with
with 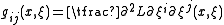 is the fundamental tensor of the Lagrangian at
is the fundamental tensor of the Lagrangian at 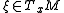 .
. - The Lagrangian satisfies the Legendre condition if the fundamental tensor
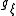 is non-degenerate at every
is non-degenerate at every  . Then the inverse matrix of
. Then the inverse matrix of 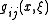 is denoted by
is denoted by 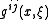 .
. - The Energy associated with the Lagrangian is
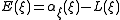 .
.
If the Legendre condition is satisfied, then dα∈Ω2(TM) is a symplectic form, and there exists a unique Hamiltonian vector field
Hamiltonian vector field
In mathematics and physics, a Hamiltonian vector field on a symplectic manifold is a vector field, defined for any energy function or Hamiltonian. Named after the physicist and mathematician Sir William Rowan Hamilton, a Hamiltonian vector field is a geometric manifestation of Hamilton's equations...
H on TM corresponding to the Hamiltonian function E such that
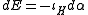 .
.Let (Xi,Yi) be the components of the Hamiltonian vector field H in the associated coordinates on TM. Then

and
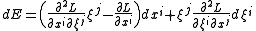
so we see that the Hamiltonian vector field H is a semispray on the configuration space M with the spray coefficients
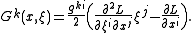
Now the first variational formula can be rewritten as
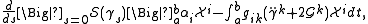
and we see γ[a,b]→M is stationary for the action integral with fixed end points if and only if its tangent curve γ':[a,b]→TM is an integral curve for the Hamiltonian vector field H. Hence the dynamics of mechanical systems are described by semisprays arising from action integrals.
Geodesic spray
The locally length minimizing curves of RiemannianRiemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
and Finsler manifold
Finsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
s are called geodesics. Using the framework of Lagrangian mechanics one can describe these curves with spray structures. Define a Lagrangian function on TM by
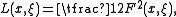
where F:TM→R is the Finsler function
Finsler manifold
In mathematics, particularly differential geometry, a Finsler manifold is a differentiable manifold together with the structure of an intrinsic quasimetric space in which the length of any rectifiable curve is given by the length functional...
. In the Riemannian case one uses F2(x,ξ) = gij(x)ξiξj. Now introduce the concepts from the section above. In the Riemannian case it turns out that the fundamental tensor gij(x,ξ) is simply the Riemannian metric gij(x). In the general case the homogeneity condition

of the Finsler-function implies the following formulae:
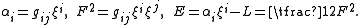
In terms of classical mechanical the last equation states that all the energy in the system (M,L) is in the kinetic form. Furthermore, one obtains the homogeneity properties
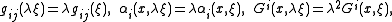
of which the last one says that the Hamiltonian vector field H for this mechanical system is a full spray. The constant speed geodesics of the underlying Finsler (or Riemannian) manifold are described by this spray for the following reasons:
- Since gξ is positive definite for Finsler spaces, every short enough stationary curve for the length functional is length minimizing.
- Every stationary curve for the action integral is of constant speed
 , since the energy is automatically a constant of motion.
, since the energy is automatically a constant of motion. - For any curve
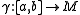 of constant speed the action integral and the length functional are related by
of constant speed the action integral and the length functional are related by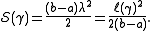
Therefore a curve
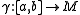 is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.
is stationary to the action integral if and only if it is of constant speed and stationary to the length functional. The Hamiltonian vector field H is called the geodesic spray of the Finsler manifold (M,F) and the corresponding flow ΦHt(ξ) is called the geodesic flow.Correspondence with nonlinear connections
A semispray H on a smooth manifold M defines an Ehresmann-connection T(TM\0) = H(TM\0) ⊕ V(TM\0) on the slit tangent bundle through its horizontal and vertical projections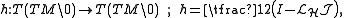
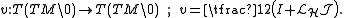
This connection on TM\0 always has a vanishing torsion tensor, which is defined as the Frölicher-Nijenhuis bracket
T=[J,v]. In more elementary terms the torsion can be defined as
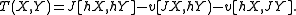
Introducing the canonical vector field V on TM\0 and the adjoint structure Θ of the induced connection the horizontal part of the semispray can be written as hH=ΘV. The vertical part ε=vH of the semispray is known as the first spray invariant, and the semispray H itself decomposes into
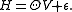
The first spray invariant is related to the tension
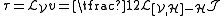
of the induced non-linear connection through the ordinary differential equation
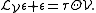
Therefore the first spray invariant ε (and hence the whole semi-spray H) can be recovered from the non-linear connection by
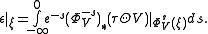
From this relation one also sees that the induced connection is homogeneous if and only if H is a full spray.

